徐兆棣，李晓毅

（沈阳师范大学 数学与系统科学学院，沈阳 110034）

0 引 言

系统的稳定性问题是人们研究自然界和人类社会中各类系统面临的最基本和最重要的问题。而稳定性分析是设计稳定的控制系统的基础，因此对系统的控制而言，稳定性问题尤为重要。

时滞系统的时滞相关稳定性分析是近年来时滞系统研究领域的一个热门重要问题，这个问题受到众多研究者的关注，并已经取得很多的研究成果［1－45］。

系统稳定性的时域分析方法主要是基于Lyapunov函数或泛函，如Lyapunov－Krasovskii泛函或Lyapunov－Razumikhin函数。它们分别是由Krasovskii和Razumikhin创立于20世纪50年代，现已成为研究时滞系统稳定性分析和控制器设计的主要方法。Lyapunov－Krasovskii泛函方法一般要比Lyapunov－Razumikhin函数方法保守性更低，因此目前在时域分析中前者的应用更多。

近年来，由于线性矩阵不等式技术在控制理论中的应用和推广，使得Lyapunov－Krasovskii泛函方法被广泛关注并已经发展的比较成熟。这主要得益于凸优化技术的发展和计算机技术的飞速发展使得线性矩阵不等式求解变得非常容易解决。目前，时滞系统稳定性分析的主要方法基本就是Lyapunov－Krasovskii泛函加线性矩阵不等式。一个主要研究的问题就是如何降低结论（主要是稳定性判据）的保守性。对时滞相关的结论而言，其稳定性条件是指系统参数所满足的条件能够保证当系统时滞小于某个时滞上界值时，系统都是稳定的。因此，最大容许的时滞上界值就成为了衡量时滞相关条件保守性的主要指标。

对时滞系统作时滞相关稳定性分析时，如何扩大系统稳定的时滞上界以达到进一步降低结论保守性的目的，是近年来控制理论界研究的热点问题。为了得到保守性更小的稳定性判据，目前使用的主要研究方法有：模型转换方法、时滞区间分割（离散Lyapunov泛函）方法、增广Lyapunov泛函方法、自由权矩阵方法、积分不等式方法等。

模型转换方法的主要思想是将一个具有离散时滞的系统通过Leibniz－Newton公式转化为一个具有分布时滞的系统，以利于处理。

时滞区间分割（包括离散Lyapunov泛函）方法主要思想是将时滞区间分割成若干子区间，然后在每个子区间研究，以利于最大程度的逼近保证系统稳定的时滞上界。但时滞区间分割方法会带来问题复杂程度和计算量的增加。

增广Lyapunov泛函方法的主要思想是为减少处理Lyapunov泛函导数中一些交叉项的困难和麻烦，把系统状态x（t）和一些相关的向量，例如x（t－d（t）），∫˙x（t）dt等组合成一个高维向量应用在Lyapunov泛函的设计中以减少处理Lyapunov泛函导数中一些交叉项放大带来的保守性。

自由权矩阵方法主要思想是将一个等式两端同乘一个适当维数的矩阵（自由权矩阵），整理后把等于0的所有项的和添加到Lyapunov泛函导数中以代替或抵消一些和时滞有关的项。在最后的时滞相关稳定性判别准则中一般会出现这些自由权矩阵，因而使得相应的矩阵不等式有解的可能性增大。但添加过多的自由权矩阵会使计算量明显增加而使得计算困难甚至无法计算。此外，已有结论证明，也不是自由权矩阵添加的多就一定可以减小保守性。

积分不等式方法主要思想是对二重积分进行界定，以降低保守性。Jensen不等式时滞系统滞相关稳定性分析中最早使用也是最常用的积分不等式。

1 一般线性时滞系统

考虑一般连续线性时滞系统：

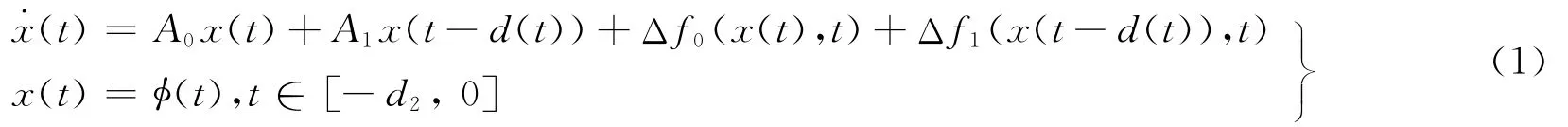
其中：d（t）为系统离散时滞，0≤d（t）≤d2；A0，A1为常值系数矩阵；Δf0（x（t），t），Δf1（x（t－d（t）），t）表示系统的不确定性扰动。通常对不确定性扰动Δf0（x（t），t），Δf1（x（t－d（t）），t）有两种约束方法：

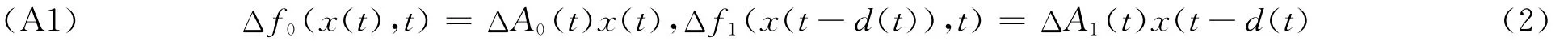
其中：ΔA0（t），ΔA1（t）表示系统的参数不确定性，

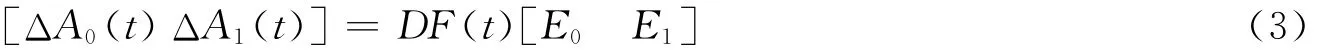
D，E0，E1为常值矩阵，F（t）为未知矩阵，满足条件

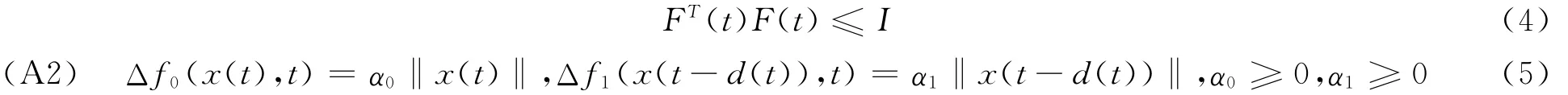
在假定（A1）下，系统（1）方程可以写为

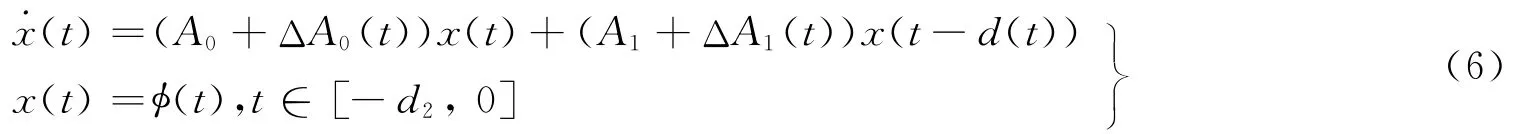
近年来，根据系统时滞d（t）满足不同条件的各种情况，研究者们给出了不同的时滞相关稳定性准则。

2004年 Wu等［1］考虑了系统（6），其中时滞d（t）是时间t的连续可微函数，并满足条件

利用Leibniz公式和自由权矩阵方法，文献［1］得到了相应的时滞相关鲁棒稳定性准则，改进了文献［14－15］2002年所得的相应结果。

同是2004年，Jing等［2］考虑了系统（6）中时滞d（t）与（8）不同的约束条件。当d（t）是时间t的连续可微函数时满足的条件放宽为˙d（t）≤d（d为任意实数）。同时文献［2］也考虑了d（t）不可微的情况。利用增广Lyapunov泛函方法得到不同约束条件下时滞相关稳定性准则。所得结论的数值仿真结果与文献［14，16］相比较保守性更小，保证系统稳定的时滞上界更大。

2008年，Peng等［3］考虑了带有区间时变时滞的系统（6），即时滞d（t）的约束条件（3）变为

同样仅仅利用增广Lyapunov泛函方法，得到不同约束条件下时滞相关鲁棒稳定性准则。所得结果具有更小的保守性，改进了文献［17－18］在2005和2006年所得的相应结果。所得结论的数值仿真结果与文献［17］相比保证系统稳定的时滞上界更大，与文献［18］相比虽然没有得到更大的保证系统稳定的时滞上界，但在计算过程中使用的变量个数更少，计算更简单。

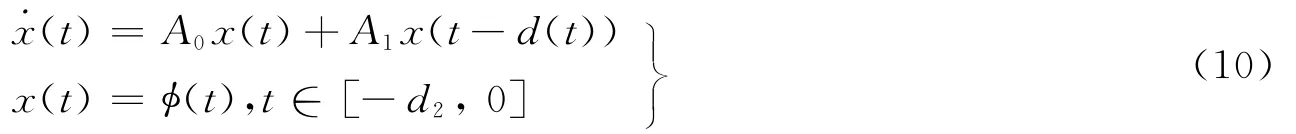
其中系统时滞d（t）满足条件（9）且（t）｜≤d的情况。利用增广Lyapunov泛函方法及一个积分不等式得到时滞相关稳定性准则。由于没有使用自由权矩阵，时滞上界的计算过程变量个数明显减少，更易于计算。改进了文献［19］在2007年所得的相应结果。所得结论的数值仿真结果与文献［17］相比保证系统稳定的时滞上界更大，与文献［20］相比虽然没有达到文献［20］在2007年所得保证系统稳定的时滞上界，但在计算过程中使用的变量个数大大减少，计算更简单。对复杂系统而言，这样的结果也是有应用价值的。

2010年，Sun等［5］考虑了系统（10），系统时滞d（t）满足条件0＜d1≤d（t）≤d2且（t）≤d的情况。利用增广Lyapunov泛函方法并首次在Lyapunov泛函中使用了三重积分项，得到了保守性更小的结果，改进了文献［21］在2009年所得的相应结果。所得结论的数值仿真结果与文献［21］相比，在时滞下界不为0的几种情况，都得到保证系统稳定的更大的时滞上界。

2010年，Park等［6］考虑了系统（10），其中系统时滞d（t）满足条件（9）且不要求d（t）可微的情况。文中提出了一种反向凸组合技术并利用此技术结果及增广Lyapunov泛函方法得到保守性较小的时滞相关稳定性准则，改进了文献［21］在2009年所得的相应结果。所得结论的数值仿真结果与文献［21］相比，在不要求系统时滞d（t）可微情况下，得到保证系统稳定的更大的时滞上界。

2011年，Park等［7］考虑了系统（10），其中系统时滞d（t）满足条件（7）且｜（t）｜≤d的情况。利用模型转换技术得到一个增广系统模型，再利用一些积分不等式及增广Lyapunov泛函方法得到了保守性更小的时滞相关稳定性准则，改进了文献［4，22］在2009年所得的相应结果。

2011年，Zhang等［8］考虑了系统（10），其中系统时滞d（t）满足条件

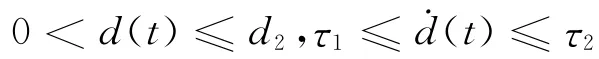
的情况。此前已有不少研究者研究时滞为常数的常时滞系统，利用时滞区间分割技术进行了讨论，得到不少好的结果［9－10］。在文献［8］中，Zhang等把时滞区间分割技术推广到时变时滞系统。利用对时滞区间进行优化分割的方法，结合线性积分技术构造增广Lyapunov泛函得到时滞相关稳定性较好的结果，改进了文献［21，23］在2009年所得的相应结果。所得结论的数值仿真结果与文献［21，23］相比，得到保证系统稳定的更大的时滞上界。

同是2011年，Wang等［11］考虑了与文献［2］相同的系统（6）且（t）≤d（d为任意实数）。利用新的积分不等式和改进的逼近方法，精确了不等式放大的精度，减少了保守性，得到保证系统稳定的时滞上界的较好结果，改进了文献［24］在2010年所得的相应结果。所得结论的数值仿真结果与文献［24］相比，得到保证系统稳定的更大的时滞上界。

2012年，Liu［12］把文献［8］的结果推广到不确定时变时滞系统。Liu考虑了系统（6），其中对系统时滞d（t）是否可微两种情况做了分别研究。同样是利用新的时滞区间分割技术进行了讨论，得到较好的结果，改进了文献［25］在2010年所得的相应结果。所得结论的数值仿真结果与文献［25］相比较保守性更小，保证系统稳定的时滞上界更大。

2011年，Ramakrishnan等［13］考虑了系统不确定性满足假定（A2），即带有非线性扰动的时变时滞系统

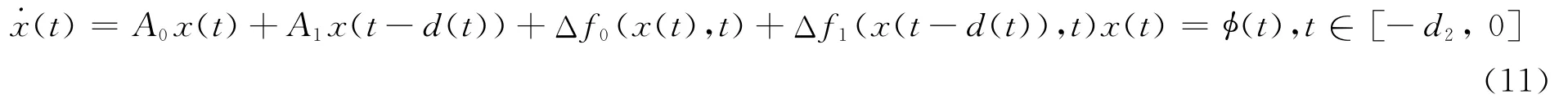
其中：Δf0（x（t），t），Δf1（x（t－d（t）），t）满足条件（5），系统时滞d（t）满足条件（9）且（t）≤d。利用时滞区间分割技术进行了讨论，得到保守性更小的时滞相关鲁棒稳定性准则，改进了文献［26］在2010年所得的相应结果。所得结论的数值仿真结果与文献［26］相比，得到保证系统稳定的时滞上界更大。

2009年，Li等［4］考虑了系统（6）的标称系统

2 中立型线性时滞系统

考虑连续中立型线性时滞系统：

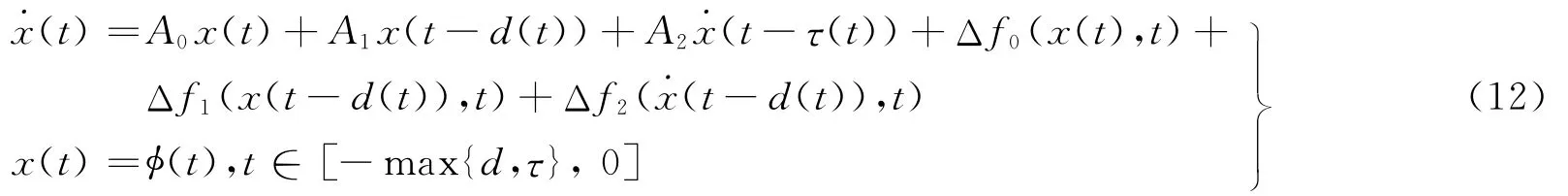
其中：d（t）为系统离散时滞；τ（t）为系统中立时滞，0≤d（t）≤d，0≤τ（t）≤τ。

类似一般时滞系统，通常对不确定性扰动 Δf0（x（t），t），Δf1（x（t－d（t）），t），Δf2（˙x（t－τ（t）），t）有两种约束方法：

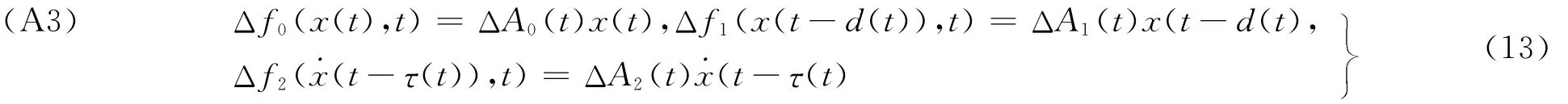
其中：ΔA0（t），ΔA1（t），ΔA2（t）表示系统的参数不确定性，

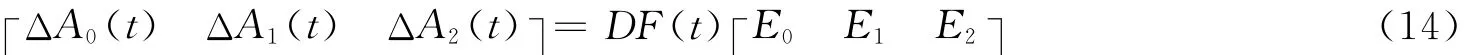
D，E0，E1，E2为常值矩阵，F（t）为未知矩阵，满足条件FT（t）F（t）≤I。

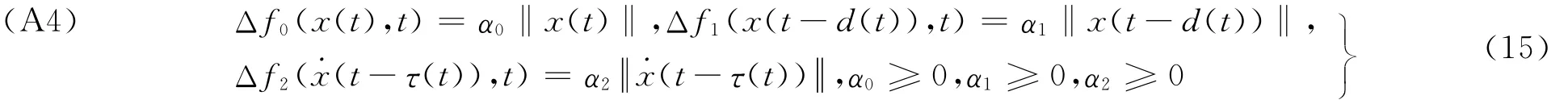
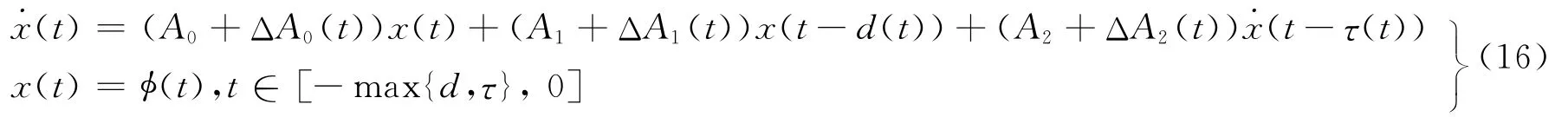
2008年，Yu等［27］考虑了系统（12），其不确定性分别满足假定（A3）和（A4）情况下系统的时滞相关稳定性。系统离散时滞和中立时滞均为时间t的连续可微函数，且满足条件（t）≤hD（t）≤τD＜1。利用Leibniz公式，自由权矩阵方法，积分不等式及设计新的Lyapunov泛函，文献［27］得到了系统不确定性分别满足不同情况下系统相应的时滞相关鲁棒稳定性准则，改进了文献［28］（2004）和文献［29］（2003）所得的相应结果。数值仿真结果与文献［28－29］结果相比，在相同中立时滞情况下，保证系统稳定的离散时滞上界更大。

2007年，Zhaog等［30］考虑了系统（16），其中Δf2（t）＝0的情况，即系统方程可以写为

由于中立型线性时滞系统包含离散时滞和中立时滞2种时滞，所以在考虑保证系统稳定的时滞上界时，通常是固定其中一个，而计算另一个时滞的上界。例如取中立时滞的几个固定值，分别计算出相应的离散时滞的上界。

在假定（A3）下，系统（12）方程可以写为

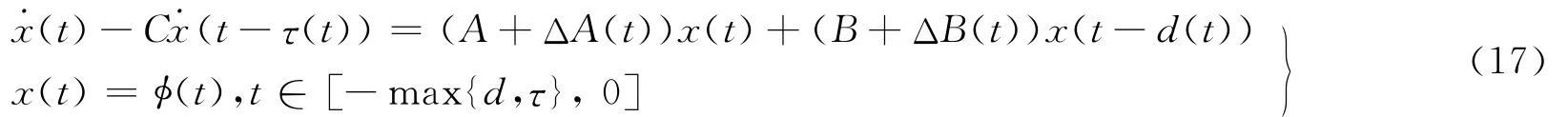
系统中立时滞τ（t）＝τ为常数，离散时滞d（t）是时间t的连续可微函数，并满足条件0≤d（t）≤d

其中d和μ是常数。利用设计新的Lyapunov泛函和积分不等式，避免使用模型转换和界定交叉项带来的保守性而得到时滞相关稳定性较好的结果，同样改进了文献［28］在2004年所得的相应结果。所得结论的数值仿真结果与文献［28］相比，在相同中立时滞情况下，保证系统稳定的离散时滞上界更大。

2008年，Liu等［31］考虑了系统（17），但条件（18）减弱为（t）≤μ＜1。利用标称系统

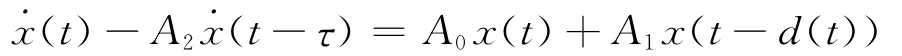
两端积分得到等式

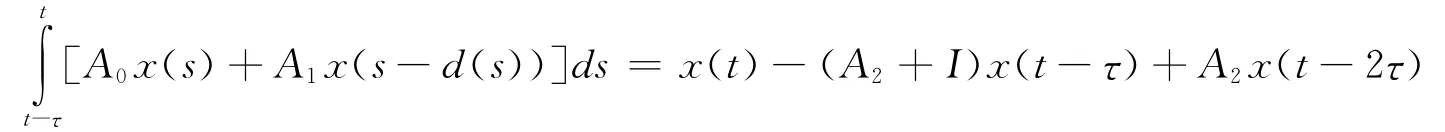
再利用Leibniz－Newton公式和自由权矩阵技术，更好的利用了系统的标称系统信息，减小了保守性，得到较好结果，改进了文献［32］在2007年所得的相应结果。所得结论的数值仿真结果与文献［32］相比，在相同中立时滞情况下，保证系统稳定的离散时滞上界更大。

2009年，Kwon等［33］考虑了系统（17），其中系统中立时滞和离散时滞是相同的时变连续可微函数，τ（t）＝d（t），满足条件0≤d（t）≤且0≤（t）≤μ＜1。经过简单的变量替换p（t）＝F（t）q（t），q（t）＝Eax（t）＋Ebx（t－d（t）），系统（16）可以写为

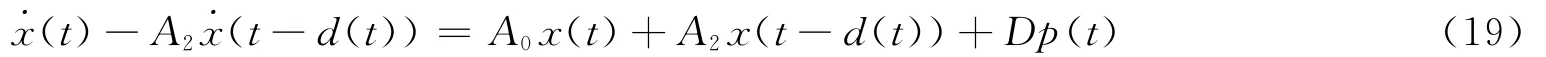
在对系统（18）设计Lyapunov泛函时利用了增广Lyapunov泛函技术，把未知向量p（t）作为增广向量的一部分，设计了增广向量ξ（t）：

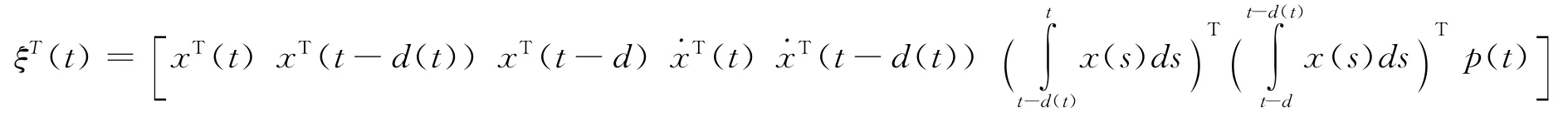
并利用增广向量ξ（t）设计了Lyapunov泛函，由于未知向量p（t）作为增广向量ξ（t）的一部分，减少了处理不确定性时的保守性，同时利用Leibniz－Newton公式和自由权矩阵技术，得到保守性更小的较好结果，改进了文献［34］在2004年所得的相应结果。所得结论的数值仿真结果与文献［34］相比，保证系统稳定的时滞上界更大。作为文献［33］的特殊情况，当系统中立时滞和离散时滞是相同常数时，其结果改进了文献［35－37］分别在2005年和2007年所得的相应结果。

2010年，Qian等［38］考虑了系统（17），其中系统中立时滞和离散时滞是不同常数的情况。利用在双积分项使用增广向量技术构造Lyapunov泛函，同时使用自由权矩阵技术，得到保守性较小的较好结果。2012年，Qian等［39］考虑了系统（17），其中系统中立时滞和离散时滞是相同常数的情况。利用增广Lyapunov泛函技术，自由权矩阵技术和积分不等式，得到保证系统稳定的更大时滞上界。同是2012年，Balasubramaniam等［40］考虑了系统（17）的标称系统，且系统中立时滞和离散时滞是相同的时变连续可微函数的情况，即

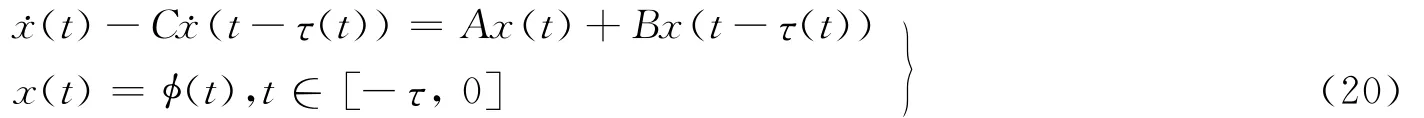
利用时滞区间分割技术，得到保守性较小的较好结果。

文献［41－43］分别考虑了系统（12），其不确定性满足假定（A4）的情况。文献［41］主要是利用自由权矩阵技术和更精确的不等式，得到保守性较小的较好结果。且所得结果不仅与系统中立时滞和离散时滞有关，而且与其导数有关。文献［42－43］主要是利用设计新的Lyapunov泛函技术，在Lyapunov泛函中引入三重积分项，同时利用积分不等式和自由权矩阵技术获得保守性较小的较好结果。

2012年，Chen等［44］考虑了带有中立时滞、离散时滞和分布时滞的中立系统：

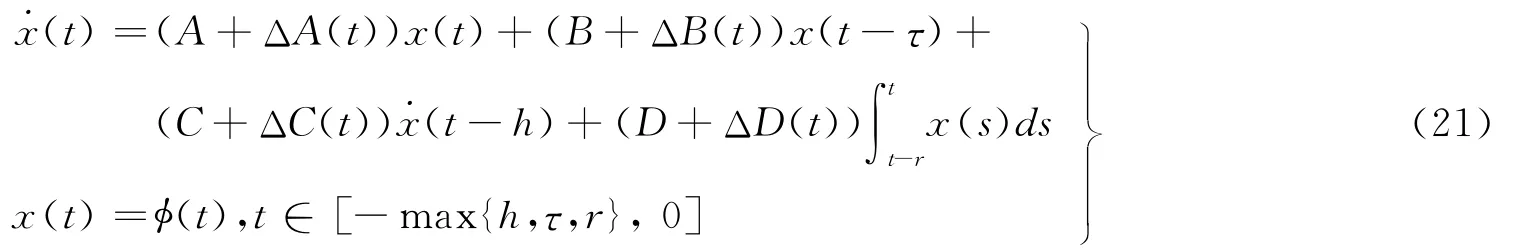
其中参数不确定性其中ΔA（t），ΔB（t），ΔC（t），ΔD（t）满足条件

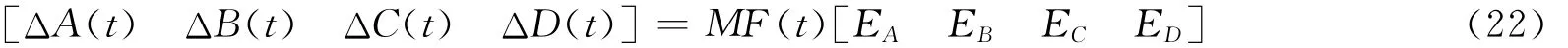
M，EA，EB，EC，ED，为常值矩阵，F（t）为未知矩阵，满足条件FT（t）F（t）≤I。利用设计新的Lyapunov泛函技术，在Lyapunov泛函中引入三重积分项，同时利用自由权矩阵技术获得保守性较小的较好结果。

时滞系统时滞相关稳定性的研究是近年来控制领域研究的热门问题，相应地研究成果也非常多。笔者仅就一般连续时滞系统和连续中立时滞系统近年的有关结果做了简单分析。此外，如时滞系统的时滞相关指数稳定性分析，时滞相关H∞稳定性分析，离散时滞系统的时滞相关稳定性分析，神经网络时滞系统的时滞相关稳定性分析等很多相关内容由于篇幅限制，没有在本文讨论。

［1］WU Min，HE Yang，SHE Jinhua，et al.Delay－dependent criteria for robust stability of time－varying delay systems［J］.Automatica，2004，40（8）：1435－1439.

［2］JING Xinghan，TAN Dalong，WANG Yuechao.An LMI approach to stability of systems with severe tims－delay［J］.IEEE Trans Automal Contr，2004，49（7）：1192－1195.

［3］PENG Chen，TIAN Yuchu.Delay－dependent robust stability criteria for uncertain systems with interval time－varying delay［J］.J Comput Appl Math，2008，214（2）：480－494.

［4］LI Tao，GUO Lei，WU Lingyao.Simplified approach to the asymptotical stability of linear systems with interval timevarying delay［J］.IET Control theory ＆ Applications，2009，3（2）：252－260.

［5］SUN Jian，LIU G P，CHEN Jie，et al.Improved delay－range－dependent stability criteria for linear systems with time－varying delays［J］.Automatica，2010，46（2）：466－470.

［6］PARK P G，KO J W，JEONG C K.Reciprocally convex approach to stability of systems with time－varying delays［J］.Automatica，2011，47（1）：235－238.

［7］PARK M J，KWON O M，PARK J H，et al.A new augmented Lyapunov– Krasovskii functional approach for stability of linear systems with time－varying delays［J］.Appl Math Comput，2011，217（17）：7197－7209.

［8］ZHANG Huaguang，LIU Zhenwei.Stability analysis for linear delayed systems via an optimally dividing delay interval approach［J］.Automatica，2011，47（9）：2126－2129.

［9］GOUAISBAUT F，PEAUCELLE D.Delay－dependent stability analysis of linear time delay systems［C］∥The sixth IFAC workshop on time－delay systems，2006.

［10］HAN Qinglong.A discrete delay decomposition approach to stability of linear retarded and neutral systems［J］.Automatica，2009，45（2）：517－524.

［11］WANG Cheng，SHEN Yi.Improved delay－dependent robust stability criteria for uncertain time delay systems［J］.Appl Math Comput，2011，218（6）：2880－2888.

［12］LIU Pinlin.A delay decomposition approach to robust stability analysis of uncertain systems with time－varying delay［J］.ISA Transactions，2012，51（6）：694－701.

［13］RAMAKRISHNAN K，RAY G.Delay－range－dependent stability criterion for interval time－delay systems with nonlinear perturbations［J］.International Journal of Automation and Computing，2011，8（1）：141－146.

［14］YUE Dong，WON S.An improvement on'Delay and its time－derivative dependent robust stability of time－delayed linear systems with uncertainty'［J］.IEEE Transactions on Automatic Control，2002，47：407－408.

［15］FRIDMAN E，SHAKED U.An improved stabilization method for linear time－delay systems［J］.IEEE Transactions on Automatic Control，2002，47：1931－1937.

［16］CHEN W Y.Some new results on the asymptotic stability of uncertain systems with time－varying delay［J］.Int J Syst Sci，2002，33（11）：917－921.

［17］XU Shengyuan，LAM J.Improved delay－dependent stability criteria for time－delay systems［J］.IEEE Transactions on Automatic Control，2005，50（3）：384－387.

［18］PARLAKCI M N A.Robust stability of uncertain time－varying state－delayed systems［J］.IEE Proc.：Control Theory Appl，2006，153（4）：469－477.

［19］HE Yong，WANG Qingguo，LIN C，et al.Delay－rang－dependent stability for systems with time－varying delay［J］.Automatica，2007，43：371－376.

［20］HE Yong，WANG Qingguo，LIN C，et al.Further improvement of free－weighting matrices technique for systems with time－varying delay［J］.IEEE Transactions on Automatic Control，2007，52：293－299.

［21］SHAO Hangyong.New delay－dependent stability criteria for systems with interval delay［J］.Automatica，2009，45：744－749.

［22］QIAN Wei，CONG Shen，SUN Youxian，et al.Nonel robust stability criteria for uncertain systems with time－varying delay［J］.Appl Math Comput，2009，215：866－872.

［23］FRIDMAN E，SHAKED U，LIU K.New conditions for delay－derivative－dependent stability［J］.Automatica，2009，45：2723－2727.

［24］YAN Huaichen，ZHANG Hao，MENG M Q.Delay－rang－dependent robustH∞control for uncertain systems with interval time－varying delays［J］.Neurocomputing，2010，73：1235－1243.

［25］QIAN Wei，WANG Lei，SUN You.Improved robust stability criteria for uncertain systems with time－varying delay［J］.Asian Journal of control，2011，13（6）：1043－1050.

［26］ZHANG Wei，CAI Xiushan，HAN Zhengzhi.Robust stability criteria for systems with interval time－varying delay and nonlinear perturbations［J］.J Comput Appl Math，2010，234（1）：174－180.

［27］YU K W，LIN Changhua.Stability criteria for uncertain neutral systems with interval time－varying delays［J］.Chaos，Solitons and Fractals，2008，38：650－657.

［28］HAN Qinglong.On robust stability of neutral systems with time－delay and norm－bounded uncertainty［J］.Automatica，2004，40：1087－1092.

［29］YUE Dong，FANG Jian'an，WON S.Delay－dependent exponential stability of a class of neutral systems with time delay and time－varying，parameter uncertainties：an LMI approach［J］.JSME Int J（Series C），2003，46：245－251.

［30］ZHAO Z R，WANG W，YANG B.Delay and its time－derivative dependent robust stability of neutral control system［J］.Appl Math Comput，2007，187（2）：1326－1332.

［31］LIU Xinge，WU Min，MARTIN R，et al.Stability analysis for neutral systems with mixed delays［J］.Journal of Comput.and Appl Math，2007，202（2）：478－497.

［32］HAN Qinglong.On stability of linear neutral systems with mixed time delays：A discretized Lyapunov functional approach［J］.Automatica，2005，41：1209－1218.

［33］KWON O M，PARK J H，LEE S M.Augmented Lyapunov functional approach to stability of uncertain neutral systems with time－varying delays［J］.Appl Math Comput，2009，207（1）：202－212.

［34］YUE Dong，HAN Qinglong.A delay－dependent stability criterion of neutral systems and its application to a partial element equivalent circuit model［J］.IEEE Transactions on Circuits and Systems－ Ⅱ，2004，51：685－689.

［35］XU Shengyuan，LAM J，ZOU Yun.Further results on delay－dependent stability conditions of uncertain neutral systems［J］.International Journal of Robust and Nonlinear Control，2005，15：233－246.

［36］PARLAKCI M N A.Robust stability of uncertain neutral systems：a novel augmented Lyapunov functional approach［J］.IET Control Theory and Applications，2007，1：802－809.

［37］PARLAKCI M N A.Delay－dependent robust stability criteria for uncertain neutral systems with mixed time－varying discrete and neutral delays［J］.Asian Journal of Control，2007，9：411－421.

［38］QIAN Wei，LIU Juan，SUN Youxian，et al.A less conservative robust stability criteria for uncertain neutral systems with mixed delays［J］.Mathematics and Computers in Simulation，2010，80：1007－1017.

［39］QIAN Wei，LIU Juan，FEI Shumin.New augmented Lyapunov functional method for stability of uncertain neutral systems with equivalent delays［J］.Math Comput Simul，2012，84：42－50.

［40］BALASUBRAMANIAM P，KRISHNASAMY R，RAKKIYAPPAN R.Delay－dependent stability of neutral systems with time－varying delays using delay－decomposition approach［J］.Applied Mathematical Modelling，2012，36（5）：2253－2261.

［41］QIU Fang，CUI Baotong，JI Yan.Further results on robust stability of neutral system with mixed time－varying delays and nonlinear perturbations［J］.Nonlinear Analysis：Real World Applications，2010，11（2）：895－906.

［42］LAKSHMANAN S，SENTHILKUMAR T，BALASUBRAMANIAM P.Improved results on robust stability of neutral systems with mixed time－varying delays and nonlinear perturbations［J］.Appl Math Model，2011，35（11）：5355－5368.

［43］KRISHNASAMY R，BALASUBRAMANIAM P，KRISHNASAMY R.Delay dependent stability analysis of neutral systems with mixed time－varying delays and nonlinear perturbations［J］.J Comput App Math，2011，235（8）：2147－2156.

［44］CHEN Huabin，ZHANG Yong，ZHAO Yong.Stability analysis for uncertain neutral systems with discrete and distributed delays［J］.Appl Math Comput，2012，218（23）：11351－11361.

［45］刘畅，徐兆棣，高杰.具有时变时滞的中立型系统的指数稳定性［J］.沈阳师范大学学报：自然科学版，2010，29（1）：4－7.