刘雄伟

（国防科技大学理学院 数学与系统科学系，湖南 长沙 410073）

准确理解和把握函数极限内涵，对学习、理解和应用微积分理论、方法有着重要意义。一元函数的极限理论相对来说比较严格与完善，多元函数极限存在性的判定与计算，由于其复杂性，还没有建立完善的理论。虽然，对非数学专业的学生来说，着重于数学的应用与支撑作用；但是，如果对二元函数极限的存在性与求解方法没有清晰的理解与思路，必然会在二元函数极限、连续、可微、方向导数存在性的判断、多元积分模型的构建与计算等概念学习与理论、方法应用的过程中，在心里留下一知半解的“心结”。因此，在二元函数极限的教学过程中，必须充分考虑学习对象的层次、特点与教学目标需求，既不能有过深的数学理论，也不能以简代全。本文将从二重极限定义出发，分析二重极限与一元函数的极限的联系与区别、二重极限与累次极限、方向极限的关系，并讨论二重极限存在性的判定方法与常见的计算方法。

1 二元函数三类极限的定义

1.1 二重极限

定义1[1]设f(x,y)是定义在点P0(x0,y0)的某去心邻域内的二元函数，A 为常数。若∀ε＞0,∃δ＞0，使得当 P(x,y)∈U0(P0,δ)时，恒有｜f(x,y)-A｜＜ε，则称 A 为 f(x,y)当(x,y)→(x0,y0)时的二重极限。

定义2[2]设f(x,y)是定义域为D的二元函数，P0(x0,y0)是D的一个聚点。如果存在常数A，∀ε＞0，∃δ＞0，使得当 P(x,y)∈U0(P0,δ)∩D 时，恒有｜f(x,y)-A｜＜ε，则称 A 为 f(x,y)当(x,y)→(x0,y0)时的二重极限。

两种定义的比较：

（1）定义1是一元函数极限的直接推广，要求函数f(x,y)在P0的某个去心邻域内每一点都要有定义，并且，对于 U0(P0,δ)中每一点，都满足不等式｜f(x,y)-A｜＜ε。定义2中允许f(x,y)在P0的任一去心邻域内有使f(x,y)无定义的点，只要求在U0(P0,δ)∩D内的点都满足｜f(x,y)-A｜＜ε。相对而言，定义 1条件太强，定义 2要求要弱，因此定义2具有更大的适用范围。例如对于二元函数

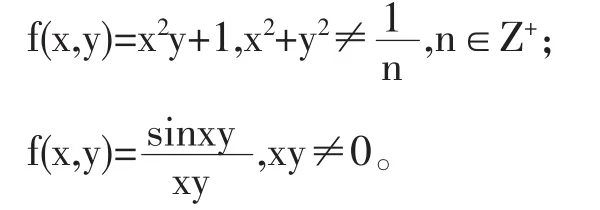
按定义1，这两个函数在(x,y)→(0,0)时，极限无意义；但按定义2，两个函数的极限都存在，并且等于1。

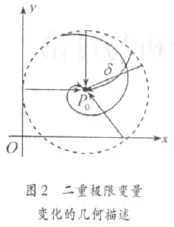
（2）两个定义与一元函数极限定义最大的区别是，在邻域内的点P趋于P0的方式不再只是两个方向，即变量沿着变量对应的坐标轴，从左右两个直线路径方向变化，如图1所示；而是点P是从任意不同方向，以任意路径趋于点P0，如图2所示，点P趋于点P0的过程不管以任何路径、任何方向变化，它们间距离始终趋于零，同时具有相同的极限值。

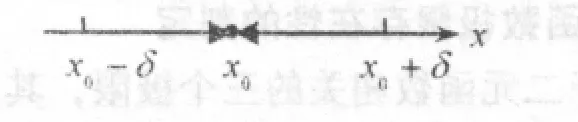
图1 一元函数极限变量变化的几何描述

1.2 累次极限

累次极限也称为二次极限，其本质上属于一元函数极限的范畴，是接连求两次一元函数的极限。f(x,y)关于变量x和y在(x0,y0)处的累次极限有两个，分别为先关于变量x后关于变量y的累次极限，记作先关于变量y后关于变量x的累次极限，记作

图3 图示

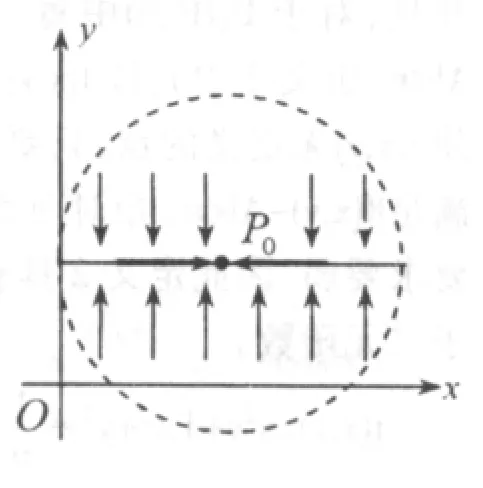
图4 图示

1.3 [3] 方向极限

设f(x,y)是定义域为D的二元函数，如果当(x,y)沿着方向为u→的射线趋于(x0,y0)时，如果二元函数的极限存在，则称该极限值A为函数f(x,y)沿着方向u→的方向极限，并记作

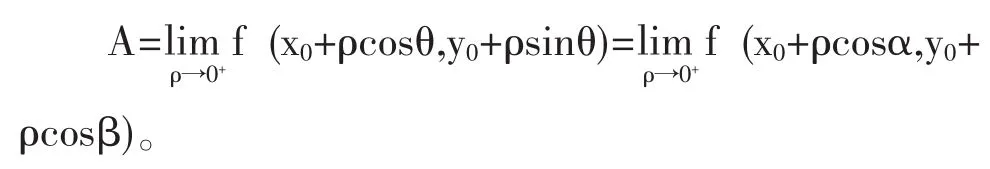
2 二元函数极限存在性的判定

对于二元函数相关的三个极限，其中累次极限本质上是一元函数极限存在性的判定，而方向极限属于二重极限的特殊情况，也可以归结为一元函数极限存在性的判定，对于这两类极限存在性判定这里不予讨论，重点讨论定义2定义的二重极限存在性判定与求解方法。

二重极限存在性的判定最基本、直接的方法是利用定义及其变型描述和借助于一元函数常用的一些判断方法，如夹逼准则、两个重要极限、函数等价变换或者转换为一元函数形式和二元初等函数的连续性、二重积分等来进行验证性判断或极限求解。

分析：当(x,y)→(0,2)时，由于在点(0,2)邻域半径δ＜2 的邻域内，变换

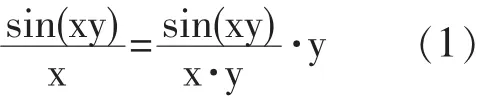
是等价变换，所以有

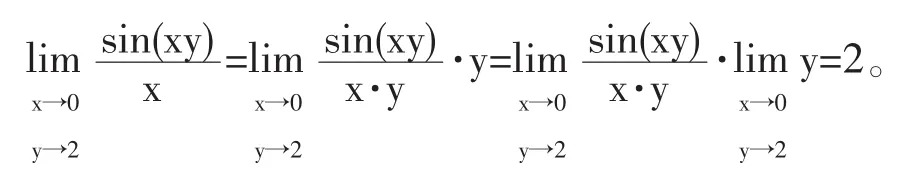
当(x,y)→(0,0)时，在点(0,0)邻域内，（1）不是等价变换，所以不能使用上面极限求解过程判断极限存在和求解极限。 而由于｜sinxy｜≤｜xy｜

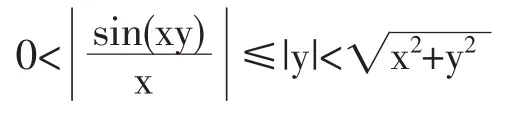
利用夹逼定理，可以得，当(x,y)→(0,0)时，f(x,y)→0。

此外，根据二元函数极限的定义，极限存在要求(x,y)→(x0,y0)时，必须按照任意方向，任意路径具有相同的极限值。因此，通过选定特定的路径，如果极限不存在；或者选择两条不同的路径，极限虽然存在但是不相等，由此可以判断二元函数极限不存在。

分析：当(x,y)沿路径 y=kx 趋于(0,0)时，有

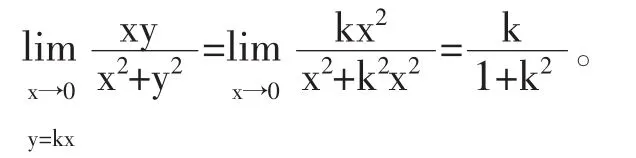
当k取不同值时，函数f(x,y)具有不同极限值。因此，可以判定该函数当(x,y)→(0,0)时极限不存在。

对于不同的二元函数如何选取特殊路径来判断函数的极限不存在是个比较复杂的问题，一般选取的路径为

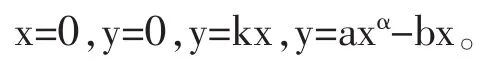
此外，对于有些二元函数，将二元函数f(x,y)转换为极坐标描述 F(ρ,θ)，通过求 ρ→0+的极限来判定极限的存在性也是一种有效方法。如例2，使用极坐标变换，则有

由于θ可取不同值时，函数具有不同的极限值，因此该极限不存在。而

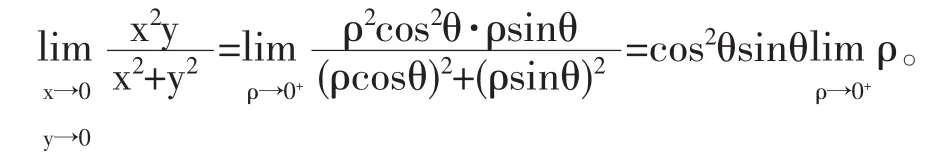
根据一元函数的极限运算法则，可知该极限存在，并且极限值为0。

由此可见，对于某些二元函数来说，使用极坐标变换不失为一种有效的二元函数极限存在性判定和求解的方法。但是，使用过程中特别要注意θ的任意性。对于更详细理论探讨与二元函数极限的求解方法及例题可以参考文献[4-8]。二元函数二重极限存在与不存在的判断也可以借助于几何图形曲面与等值线图进行观察，如例2中的函数，图形（如图6所示）在原点断裂，而等高线都为直线，直观的看出其在原点没有极限。

图5 方向极限

图6 等值线图

3 二元函数各类极限之间的关系

二元函数的二重极限、两种顺序的累次极限与方向极限之间关系相对于一元函数左右极限的讨论来说要复杂，下面是相关的结论。

（1）二重极限与两种顺序的累次极限：如果它们都存在，则三者相等，仅知其中一个存在，推不出其它二者存在。如例2，两种顺序的累次极限都存在，并且等于0，但二重极限不存在；对于二元函数f(x,y)在(x,y)→(0,0)时，两种顺序的累次极限都不存在，但二重极限存在；二元函数f(x,y)=当(x,y)→(0,0)时，二重极限不存在，两种顺序的累次极限都存在，但是极限值不想等。

（2）两种顺序的累次极限：不一定同时存在；若两者都存在，二者也不一定相等。

（3）二重极限和方向极限：二重极限存在，则方向极限一定存在，并且极限值相等。但是，即使所有方向极限存在，二重极限也不一定存在，如例2，当(x,y)→(0,0)时，沿任意方向u→°=(cosθ，sinθ)，方向极限都存在，且为cosθsinθ，但二重极限不存在；而如果有一个方向的方向极限不存在或者沿两个不同的方向极限值不相等，则根据定义，二重极限不存在。

（4）方向极限与两种顺序累次极限：方向极限存在不能推出两种顺序的累次极限存在相等；同样，两种类型的累次极限存在也不能推出所有方向的方向极限存在。

[1]朱健民，李建平.高等数学（下册）[M].北京：高等教育出版社，2007.

[2]同济大学应用数学系.高等数学（下册）[M].北京：高等教育出版社，2007.

[3]吉林大学数学系.数学分析（下册）[M].北京：人民教育出版社，1978.

[4]桂咏新.二元函数极限不存在的判别[J].咸宁师专学报(自然科学版)，1997，17，(3)：18-19.

[5]孙千高.二元函数极限的存在性[J].青海大学学报（自然科学版），2005，23，(2)：77-80.

[6]闰红霞.二重极限不存在的一种证明方法[J].高等数学研究，2011，14，(2)：27-28.

[7]庄兴义.二元函数极限不存在性问题之研究[J].广西梧州师范高等专科学校学报，1999，15，(3)：59-61.

[8]辛春元.二重极限计算方法的研究[J].长春教育学院学报，2011，27，(7)：86-88.