蹇 红，孙春涛

（重庆邮电大学数理学院，重庆 400065）

对CN－环与CT－内射的一些讨论

蹇 红，孙春涛

（重庆邮电大学数理学院，重庆 400065）

文章给出了CN－环、CT－内射及CT－内射维数的定义与性质，讨论了CN－环与GN－环以及CT－内射与自内射环的关系.

CN－环；CT－内射；CT－内射维数；无挠模；循环模

0 引 言

文［1］指出：环R是左noetherian环⇔f.g左R－模f.p.文［2］指出：环R是左coherent环⇔f.p左R－模的子模是f.p⇔f.p右R－模的对偶模是f.g左R－模.文［3］指出：环R是左Π－coherent环（也称GN－环）⇔f.g无挠左R－模f.p⇔f.g右R－模的对偶模是f.g左R－模.在左Π－coherent环上已经得到了大量的性质［4－5］.本文主要对CN－环、CT－内射模和CT－内射维数的概念和性质展开讨论.

本文所涉及的环均带有单位元，模均指酉模.用f.g表示有限生成模，用f.p表示有限表现模，用A＊表示A的对偶模HomR（A，R），δM表示同态M→M＊＊，当δM是单同态时，称M是无挠模，当δM同构时，称M是自反模，r（L）＝｛r∈R｜ar＝0，∀a∈L｝表示左理想L的零化子，l（I）＝｛r∈R｜ra＝0，∀a∈I｝表示右理想I的零化子.

下面给出本文所需要的概念.

定义1［6］设K是左R－模的A子模，称K是A的闭子模，若A/K是无挠模.

定义2［7］称环R是D－环，若对任给的右理想I，有rl（I）＝I和任给的左理想L，有lr（L）＝L.

定义3［8］称环R是右（左）P－内射，如果对每个同态f：aR（Ra）→R，都可提升R到R的一个同态上.

1 CN－环的基本性质

定义4 称环R是右CN－环，若R的任给循环左R－模的对偶模是有限生成右R－模.

定理1 设R是环，则下列条件是等价的：

（1）环R是右CN－环；

（2）循环无挠左R－模f.p；

证明 （1）⇒（2） 设M是循环无挠模左R－模，有正合列0→T→R→M→0，且有正合列0→M＊→R＊→U→0，其中U是循环模，则有下列交换图：

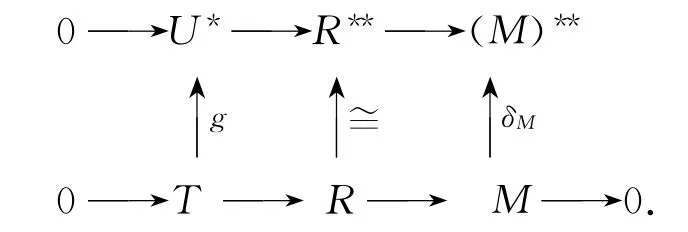
因δM是单同态，由文［1］三引理知，g是满同态，又由五引理知g是同构，即T≅U＊，故T是f.g，M是f.p.

（2）⇒（1） 设M是循环左R－模，有正合列0→K→R→M→0，则有正合列0→M＊→R＊→L→0，其中L是K＊的循环无挠子模，是f.p模，故M＊是f.g模.

性质1 设R是右P－自内射环，则R是右CN－环⇔R是右GN－环.

证明 设R是右CN－环，设M是f.g左R－模，设x1，x2，…，xn是模M的最小生成元集.当n＝2时，有正合列0→x1R→M→x1R/（x1R∩x2R）→0，因设R是右P－自内射环，则有正合列0→x1R/（x1R∩x2R）＊→M＊→（x1R）＊→0，因循环模的对偶模（x1R/（x1R∩x2R））＊和（x1R）＊是f.g，则M＊也是f.g.当n＝k时，设M＊也是f.g的，当n＝k＋1时，设M＝x1R＋M1，其中M1最小生成元的个数是k，则有正合列0→M1→M→x1R/（x1R∩M1）→0，类似上述证明可得M＊也是f.g的，故R是右GN－环.反之，显然成立.

推论1 若环R是右CN－环，M是循环左R－模，则M无挠⇔M是f.g自由模的子模.

证明 设M是循环无挠左R－模，则M＊是f.g模，有正合列F→M＊→0，其中F是f.g自由模，则有正合列0→M＊＊→F＊，因M是循环无挠模，则有正合列0→M→F＊，故M是f.g自由模的子模.反之，显然成立.

推论2 若环R的每个右理想的左零化子理想是f.g，则R是右CN－环.

证明 因任给的循环左R－模M，有正合列0→l（I）→R→M→0，则M是f.p.

2 CT－内射模，CT－内射维数

性质2［6］对左理想L，R/L是无挠模当且仅当lr（L）＝L.

性质3［6］若环R的Jacobson根是幂零的，则下列条件等价：

（1）对任意左理想L和右理想I，R/L和R/I都是自反的；

（2）每个f.g左R－模和每个f.g右R－模都是自反的；

（3）RR和RR都是内射的且R满足零化子条件；

（4）R是QF环.

定义5 称MR是右CT－内射模，如果对任给的循环无挠N，有Ext1R（N，M）＝0.称环R是右CT－内射环，如果对任意的循环无挠NR，有Ext1R（N，R）＝0.MR的CT－内射维数是inf｛n｜Extn＋1R（N，M）＝0｝（其中NR是任给的循环无挠右R－模），记为CT－inj.dimMR.称sup｛CT－inj.dimMR，∀MR｝为R的CT－内射维数，记为rCT－I.dimR.类似地，可定义左CT－内射模，左CT－内射环和左CT－内射维数.

定理2 下列条件是等价的：

（1）MR是右CT－内射；

（2）对任给的R的左理想L，有Ext1R（R/r（L），M）＝0；

（3）如果K是R的闭右理想，则K到M的每个右R－模同态，均可扩张成R到M的右R－模同态.

证明 （1）⇒（2） 因对任给的R的左理想L，R/r（L）都是无挠模，且是循环模，由CT－内射的定义，（2）成立.

（2）⇒（1） 对任给的循环无挠右R－模N，存在一个左理想L，使得N≅R/r（L），得证.

（1）⇒（3） 由闭子模的定义得证.

（3）⇒（1） 显然成立.

定理3 设R是环，则下列条件等价：

（1）R是右CT－内射环；

（2）对任给的R的左理想L，有Ext1R（R/r（L），R）＝0；

（3）任给的循环无挠左R－模是自反模.

证明 （1）⇔（2） 由定理2可得.

（2）对任给的R的右理想I，R是右CT－内射环且I到R的任何一个同态都能提升到rl（I）当且仅当R是左自内射环.

证明 （1）任给的正合序列0→M→N→P→0，其中P是循环无挠右R－模，则有正合列0→HomR（P，M）→HomR（N，M）→HomR（M，M）→0，可知存在g∈HomR（N，M），使IM＝fg，故正合序列可裂.

（2）假设R是右CT环，由性质2知，（R/rl（I），R）＝0，故任意rl（I）到R的同态都能提升到R.反之易证.

性质5 下列条件等价：

（1）R是右CT－内射环，且R满足左零化子条件；

（2）任给的循环左R－模是自反模；

（3）R是右自内射环，且R满足左零化子条件.

证明 （2）⇒（1） 设任给的循环左R－模M都是自反模，且M≅R/L，其中L是R的左理想，由性质2知R/L是自反的当且仅当lr（L）＝L且（R/r（L），R）＝0，则知R是右CT环，且R满足左零化子条件.

（1）⇒（2），（1）⇔（3）显然.

定理4 若环R的Jacobson根是幂零的，则下列条件等价：

（1）对任意左理想L和右理想I，R/L和R/I都是自反的；

（2）每个f.g左R－模和每个f.g右R－模都是自反的；

（3）RR和RR都是CT－内射的且R满足零化子条件；

（4）RR和RR都是内射的且R满足零化子条件；

（5）R是QF环.

证明 由性质2与性质5即证.

性质6 设R是右CN环，则下列条件等价：

（1）CT－inj.dimMR≤n；

（2）（A，M）＝0，其中A是任给的循环无挠右R－模；

（3）若0→M→E0→E1→En→0是正合列，且Ei（0≤i≤n－1）是CT－内射，则En也是CT－内射.

证明 由CT－内射的定义可得.

定理5 设R是环，则下列条件等价：

（1）CT－inj.dimRR≤1；

（2）对任给的循环无挠右R－模N，Ext1R（N＊，R）＝0；

（3）Ext1R（lr（L），R）＝0，其中L是任给的左R理想.

证明 （1）⇒（2） 设N是任给的循环无挠右R－模，有正合列0→K→R→N→0，则有正合列0→N＊→R＊→B→0；其中B是循环无挠左R－模，则有正合列由CT－inj.dimRR≤1知

（2）⇒（1） 对任给的循环无挠左R－模N，由定理3的证明知，有正合列0→B＊→R→N→0，其中B是循环无挠R－模，则有正合列即CT－inj.dimRR≤1.

（2）⇔（3） 显然.

［1］Lam T Y.Lectures on modules and rings［M］.New York：Springer－Verlag，1999：56－57.

［2］Colby R R.Rings which have flat injective modules［J］.J Algebra，1975，35：239－252.

［3］汪明义.GN－环上的对偶模［J］.广西师范大学学报：自然科学版，1991，9（2）：11－14.

［4］Wang Mingyi.Some studies onΠ－coherent rings［J］.Proceedings of the American Mathmatical Society，1993，119（1）：71－75.

［5］Wang Mingyi.Π－coherent rings and FGT－injective dimension［J］.Sea Bull Math，1995，19（3）：105－112.

［6］Hyman B.Finitistic dimension and a homological generalization of semi－primary rings［J］.Trans Amer Math Soc，1960，95：466－488.

［7］Hajarnavis C R，Norton N C.On dual rings and their modules［J］.J Algebra，1985，93：253－266.

［8］章聚乐，陈建龙.P－内射环和半素环［J］.数学杂志，1991，11（1）：29－34.

OnCN－rings andCT－injective Rings

JIAN Hong，SUN Chun－tao

（School of Mathsmatics and Physics，Chongqing University of Posts and Telecommunications，Chongqing 400065，China）

The paper provided the definition and properties ofCN－rings，CT－injective rings andCT－injective dimensions，and discussed the relations between theCN－rings andGN－rings as well as the relations betweenCT－injective rings and selfinjective rings.

CN－rings；CT－injective rings；CT－injective dimensions；torsionless modules；cyclic modules

O153.3 MSC2010：16D50；16E10

A

1674－232X（2012）06－0516－04

10.3969/j.issn.1674－232X.2012.06.008

2012－06－04

蹇 红（1980—），女，讲师，主要从事环论研究.E－mail：jianhong＠cqupt.edu.cn