王玉龙，欧阳洁，王晓东，蒋 涛

（西北工业大学 理学院应用数学系，陕西 西安710129）

0 引 言

在流动问题中，对流扩散方程具有非常重要的地位。如何消除数值方法在对流占优时出现的数值伪振荡，一直是学者们关心的重点。目前，基于网格的数值方法是数值求解流动问题的主流方法，如有限差分法（Finite Difference Method，FDM）、有限元法（Finite Element Method，FEM）和有限体积法（Finite Volume Method，FVM）等，但此类方法得到的数值结果与网格质量有关，且复杂三维结构的有限元网格剖分也非常困难。

无网格方法是近年来发展起来的一类新的数值方法，该类方法基于点近似，不需要将节点连成单元，克服了网格类方法遇到的一些困难。其中，无单元Galerkin（Element Free Galerkin，EFG）法［1－4］由 于精度高、稳定性好等优点而备受学者青睐。标准的EFG方法需要在背景网格上计算积分，由于无网格近似函数不是多项式，积分不能精确计算，一般需要用到较高阶的 Gauss积分［2，4］，从而增加了计算量。另外，运用标准的EFG方法求解对流占优的流动问题时会出现非物理的数值伪振荡现象［5］。

针对EFG方法计算量大的问题，一些学者提出了采用节点积分代替背景网格积分的方法。其中，Beissel等人［6］提出了直接节点积分方法，但该方法精度较低，稳定性较差。Nagashima［7］提出了基于局部Taylor展开的节点积分方法，解决了在结构分析中直接节点积分不稳定的问题，但Nagashima的方法在计算积分权值时要构造类似背景网格的“Bucket”。Liu等人［8］提出了基于全局Taylor展开的节点积分方法，然而该方法需要计算形函数的三阶导数。Dyka等人［9］提出了应力点积分，该方法需要添加辅助应力点，计算量是直接节点积分的两倍左右。Chen等人［10］提出了稳定协调的节点积分方法，该方法需要在各节点子域的边界上进行积分，增加了节点积分的计算量。此外，针对EFG方法求解对流占优问题时出现的数值伪振荡现象，欧阳洁等人［5］建立了一系列稳定化方案，但在稳定化方案中需要确定稳定化参数。

基于目前的研究现状，本文采用局部Taylor展开思想，建立了局部Taylor展开积分无单元Galerkin（Local Taylor Expansion Integration Element Free Galerkin，LTEI－EFG）法，并首次将该方法用于求解对流占优的流体力学问题。与采用背景网格积分的EFG方法相比，LTEI－EFG法能够明显提高计算效率且有效抑制由于对流占优引起的数值伪振荡。

1 控制方程和EFG方法的基本原理

1.1 控制方程

非稳态对流扩散方程的一般形式为［11］：

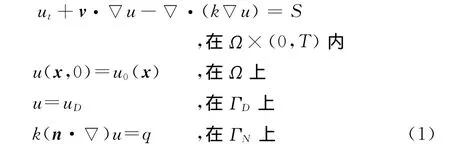
其中，v（x，t）是速度场，k（x，t）是扩散系数，s（x，t）是源项，若u（x，t）与时间t无关，则方程（1）是稳态对流扩散方程。

1.2 EFG方法的基本原理

在函数近似和空间离散时分别采用移动最小二乘法（Moving Least Square，MLS）和Galerkin法，则得到EFG方法［1］。下面针对方程（1）给出EFG方法的基本原理。

1.2.1 解的近似方案

设函数u（x，t）的MLS近似表达式为：

其中a（x，t）是待定向量，p（x）为基函数向量，m为基函数个数。基函数向量p（x）通常采用Pascal三角形所决定的单项式以确保其最小完备性［2］，本文采用线性基，即pT（x）＝（1，x）（m＝2，in1D），pT（x）＝（1，x，y）（m＝3，in2D）。

式（2）中的待定向量a（x，t）满足离散加权L2范数达到最小，即a（x，t）由

确定。其中n是点x支持域内的节点个数，ui（t）是节点参数，w（x－xi）是紧支权函数。局部Taylor展开积分需要计算形函数的二阶导数，而权函数的连续性直接影响到形函数的连续性［1－4］，本文取三次样条函数［2，4］作为权函数。

式（3）关于a（x，t）最小化得如下线性方程组：

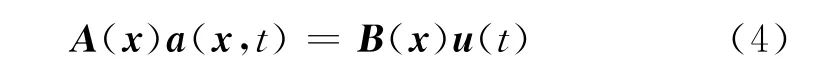
其中A＝pT（x）W（x）p（x）

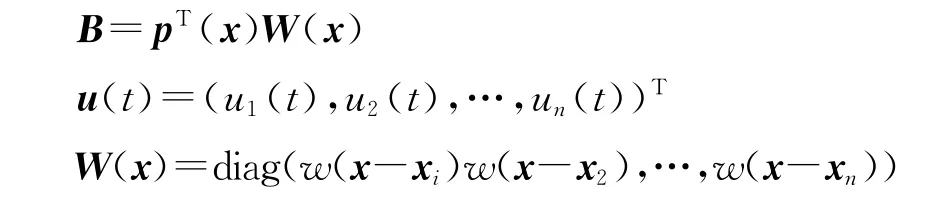
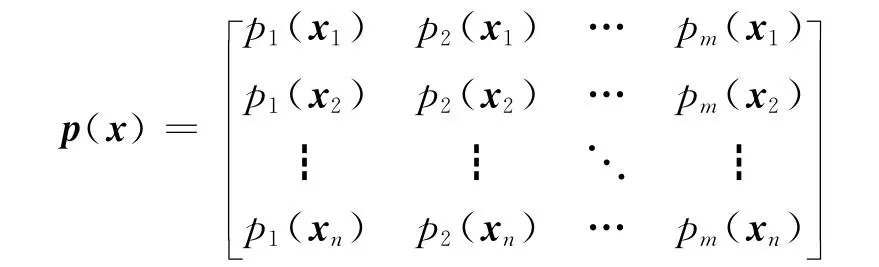
如果A（x）可逆，则a（x，t）＝A－1（x）B（x）u（t），将a（x，t）代入式（2），得：

其中N（x）是MLS形函数矩阵。

1.2.2 方程离散方案

为简单起见，本文采用θ加权法［9］进行时间离散，其它时间离散方法可参见有关文献［9］。

应用θ加权法，方程（1）可写为以下形式：

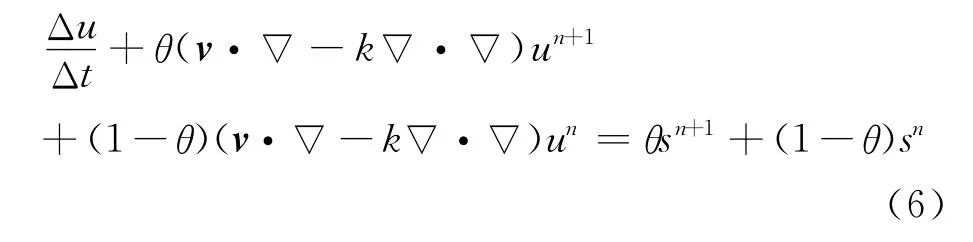
其中 Δu＝un＋1－un，v＝（un，vn）。当θ＝1／2时为Crank－Nicolson格式，该格式在时间域上具有二阶精度。本文算例均取θ＝1／2。

运用Galerkin原理进行空间离散，则方程（6）的弱形式为：

其中ω∈是检验函数，取为MLS形函数，

2 局部Taylor展开的节点积分方案

本文基于局部Taylor展开计算式（7）中的积分，并将采用局部Taylor展开积分的EFG方法记为LTEI－EFG。

2.1 局部Taylor展开

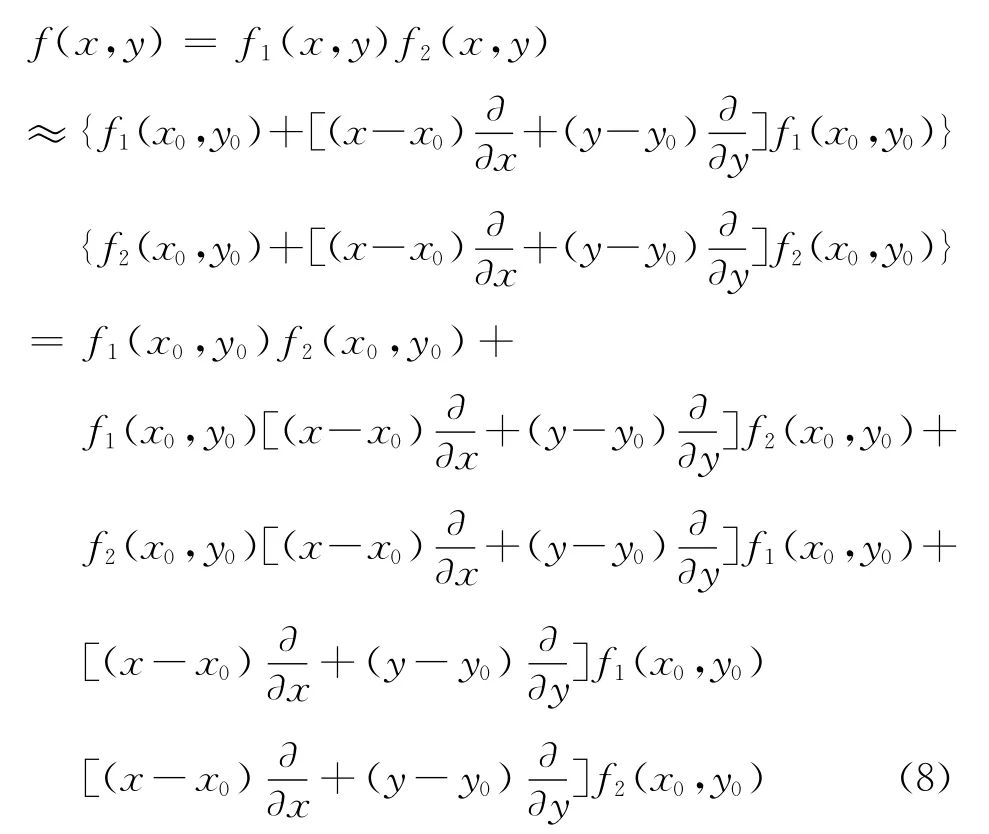
2.2 局部Taylor展开的节点积分

由式（7）知，需要计算下列积分：

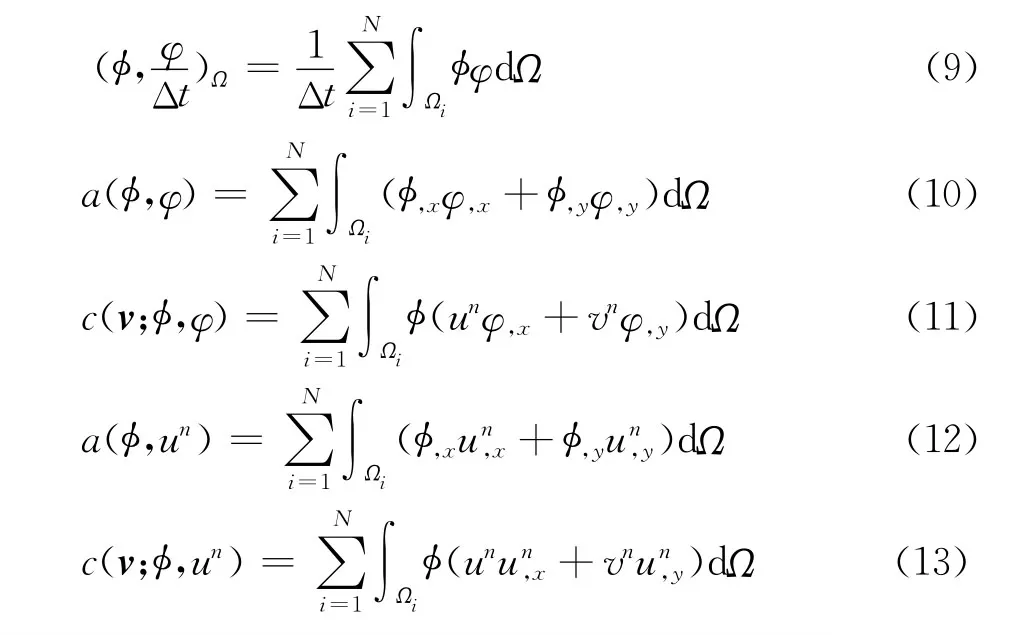
其中Ω＝∪，Ωi∩Ωj＝Φ，i≠j，且每个Ωi（i＝1，2，…，N）包含一个节点，式（9）是时间项积分，式（10）和式（12）是扩散项积分，式（11）和式（13）是对流项积分。

对任意节点 （xi，yi）∈Ωi，下面分别以y）dΩ和（x，y）dΩ为例介绍局部 Taylor展开的节点积分，其计算公式如下：

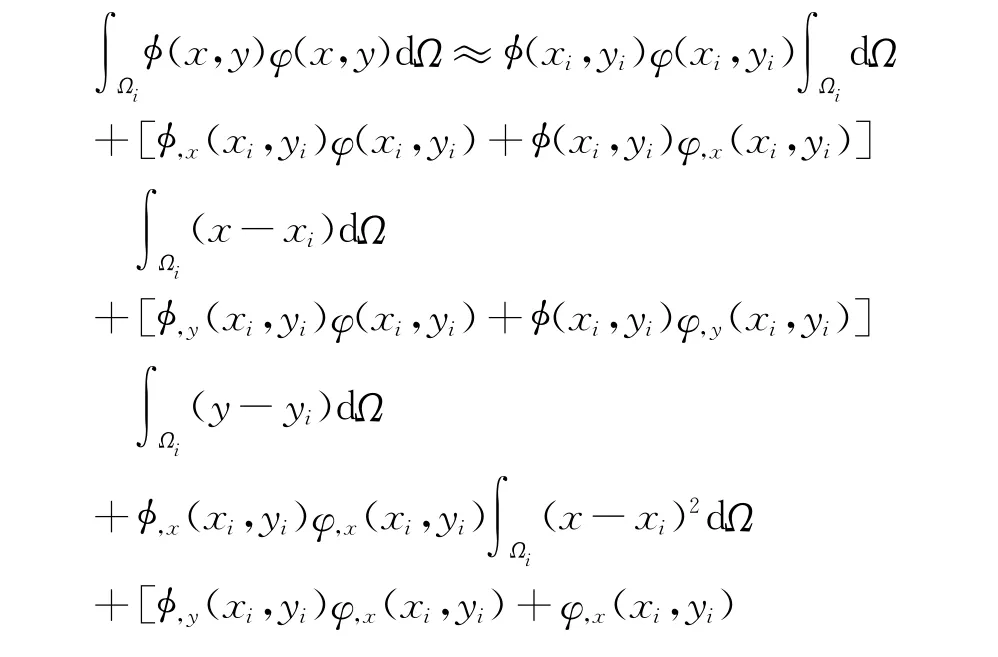
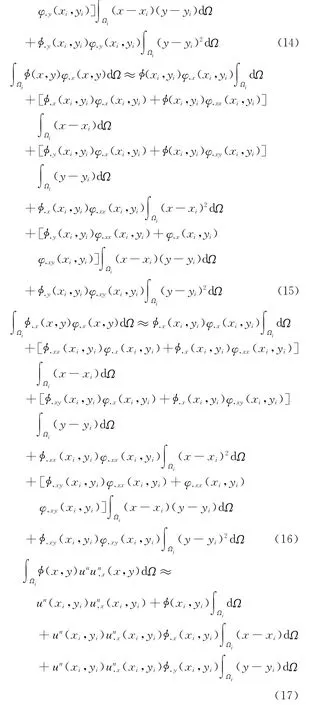
定义式（14）～式（17）中的积分权系数如下：

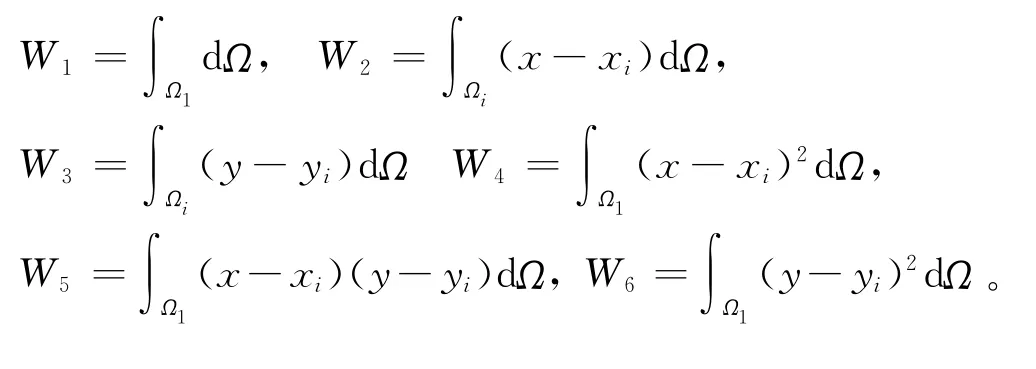
权系数的确定将在2.3节介绍。

局部Taylor展开积分公式中包含了形函数的二阶导数。一方面，该二阶导数是在对被积函数做一阶近似时出现的，与直接节点积分的零阶近似相比，提高了计算精度；另一方面，二阶导数具有稳定化的作用，能够有效消除对流占优导致的数值伪振荡。

2.3 权系数的确定

本文采用矩形支持域，且设x方向和y方向平均节点间距均为Δx。对任意节点（xi，yi），其影响半径为dri，支持域半径为dri·Δx，当（xi，yi）是内节点时取对应的子区域Ωi为圆形，当（xi，yi）是边界节点时取对应的子区域Ωi为扇形，则节点（xi，yi）处权系数W1的计算公式如下［6］：

其中MΩ是区域Ω的面积，Ν′是节点个数，fi＝，对内节点θ＝2π，θ＝0，对边界节点θ和θ FBFB是扇形区域对应的角度，如图1所示［7］。

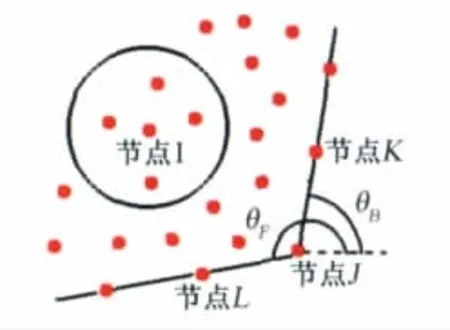
图1 权系数示意图Fig.1 Schematic diagram of the weight coefficient

下面采用文献［7］的方法计算W2：

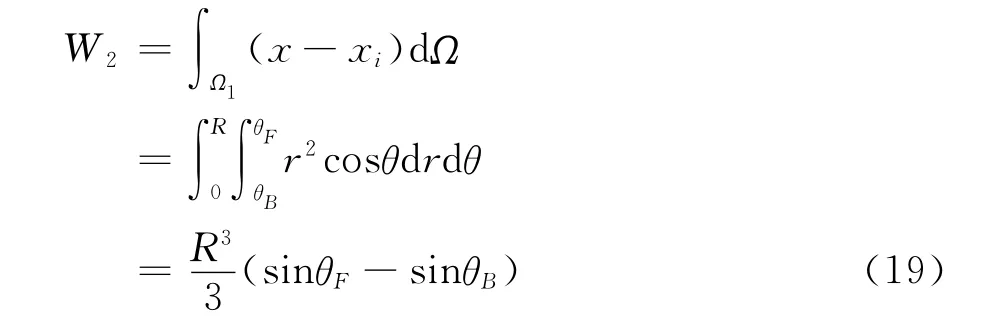
同理可得W3、W4、W5和W6的计算公式如下：

在式（19）～式（23）中，R

3 数值算例

下面通过两个数值算例检验LTEI－EFG法和采用直接节点积分的EFG方法的计算效果。将采用直接节点积分的EFG方法记为NI－EFG。本文算例均在Intel Pentium 4CPU 2.60GHz PC机上计算。

3.1 一维定常对流扩散问题

考虑一维定常对流扩散方程［11］

其精确解为u（x）

图2给出了分别取a＝1.0、v＝0.1和a＝1.0、v＝0.01时用EFG方法、NI－EFG法和LTEI－EFG法计算的数值解和精确解的比较。计算时在［0，1］区间内均匀布置31个节点，EFG方法用30个积分背景网格，每个积分背景网格用5点Gauss积分，影响半径为1.2，NI－EFG法和LTEI－EFG法的影响半径均为1.5。由图2可见，当v较大时，EFG方法和LTEIEFG法的数值解与精确解吻合很好，而NI－EFG法的数值解出现不稳定现象［6］；当v较小时，EFG方法和NI－EFG法的数值解均出现了数值伪振荡，且NI－EFG法的伪振荡更加剧烈，而LTEI－EFG法的数值解并未出现伪振荡。因此可知，（1）扩散占优时EFG方法有很好的计算精度，但对流占优时EFG方法的数值解会出现数值伪振荡［12］；（2）扩散占优时 NIEFG法的数值解存在不稳定问题，对流占优时NIEFG法的数值解会出现数值伪振荡，且比EFG方法的数值伪振荡更剧烈；（3）扩散占优或对流占优时LTEI－EFG法的数值解均未出现数值伪振荡，与精确解一致。

图2 EFG方法、NI－EFG法和LTEI－EFG法的数值解和精确解的比较Fig.2 Comparison of between exact solution and numerical solution for EFG、NI－EFG and LTEI－EFG

表1比较了取不同节点数计算时EFG方法、NIEFG法和LTEI－EFG法组装刚度矩阵花费的时间，其中EFG方法分别采用3点和5点Gauss积分。由表1可见，LTEI－EFG法和NI－EFG法组装刚度矩阵花费的时间基本相同，且均小于采用3点和5点Gauss积分的EFG方法。

表1 不同节点数时组装刚度矩阵的CPU时间（单位：ms）Table 1 CPU time of estimating stiffness matrix for different nodes（unit：ms）

为了对LTEI－EFG法进行精度分析，采用如下的相对误差［2］：

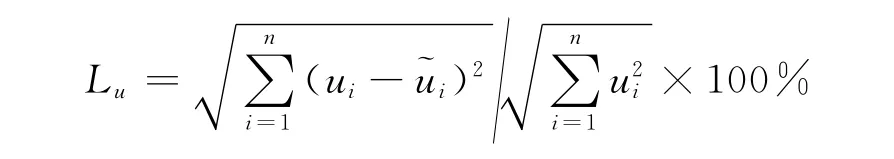
式中为节点i处的函数数值解，ui为节点i处的函数精确解。

取v＝0.1，在［0，1］区间内分别均匀布置11、21、41、81、161、321、641和1281个节点计算，结果如表2所示，其中收敛率计算公式见文献［2］。由表2可见，采用线性基的LTEI－EFG法仍然具有很高的收敛率，这是由于权函数的使用使得MLS近似形函数具有高阶光滑性［2，4］。

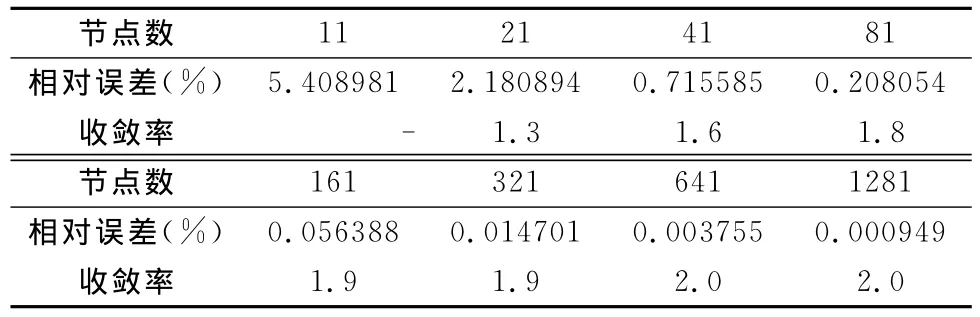
表2 LTEI－EFG法的收敛率Table 2 Rate of convergence for LTEI－EFG method

3.2 二维非定常对流扩散问题

考虑二维Burgers方程［11］：

其中u和v分别是沿x轴和y轴的速度，Re是Reynolds数，（x，y，t）∈Ω×（0，T］，Ω＝（0，1）×（0，1），该方程具有如下对称性：u（x，y，t）＝v（y，x，t），u（x，y，t）＝－u（1－x，1－y，t），下面只给出u的计算结果。

图3～图5分别给出了Re＝200时，用EFG方法、NI－EFG法和LTEI－EFG法求解时在不同时刻的数值解。此时Burgers方程中的对流项占优，在过点（0，1），（1，0）的对角线上将会产生间断。

图3 EFG方法在不同时刻的数值解（Re＝200）Fig.3 Numerical solution of EFG method for different times（Re＝200）

计算时均匀布置21×21个节点，时间步长为0.01s，EFG方法用3×3Gauss积分，影响半径为1.2，NI－EFG法和LTEI－EFG法的影响半径均为1.5。由图3和图4可见，EFG方法和NI－EFG法的数值解均出现了非物理的数值伪振荡，且NI－EFG的伪振荡更加剧烈。由图5可见，LTEI－EFG法明显抑制了数值伪振荡，其数值解与文献［12］的结果吻合。

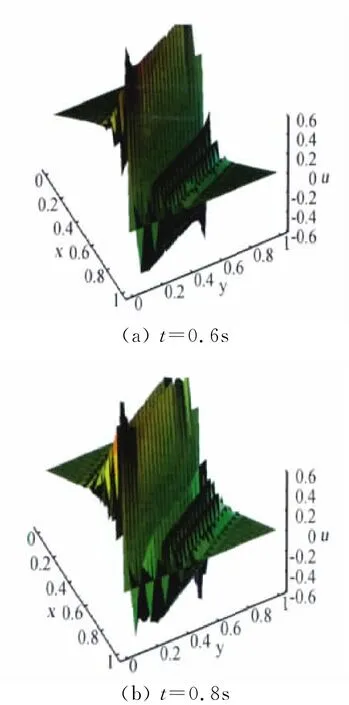
图4 NI－EFG法在不同时刻的数值解（Re＝200）Fig.4 Numerical solution of NI－EFG method at different times（Re＝200）

图5 LTEI－EFG法在不同时刻的数值解（Re＝200）Fig.5 Numerical solution of LTEI－EFG method at different times（Re＝200）

表3比较了EFG方法、NI－EFG法和LTEI－EFG法在不同时间步长下计算到t＝1.0s时组装刚度矩阵花费的时间，其中均匀布置21×21个节点，EFG方法分别采用3×3和5×5Gauss积分。由表3可见：（1）随着时间步长的减小，组装刚度矩阵的次数增加，因而花费的时间越多；（2）LTEI－EFG法和 NI－EFG法组装刚度矩阵花费的时间基本相同，且均远小于采用3×3点和5×5点Gauss积分的EFG方法。

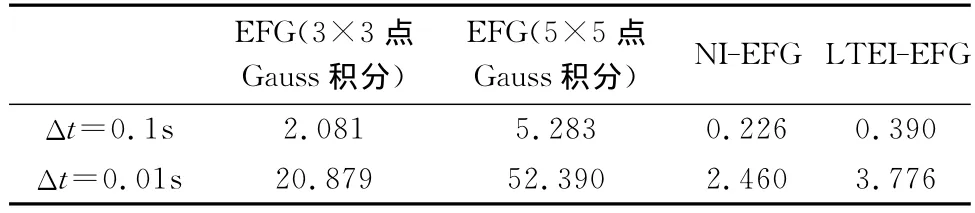
表3 不同时间步长时组装刚度矩阵的CPU时间（单位：s）Table 3 CPU time of estimating stiffness matrix for different time step（unit：s）

由表1和表3可见，一维情况下LTEI－EFG法需要的计算时间大约是采用3点Gauss积分EFG方法的40%；二维情况下LTEI－EFG法需要的计算时间大约是采用3×3Gauss积分EFG方法的18%。因而，LTEI－EFG法大幅度提高了采用背景网格积分EFG方法的计算效率，且问题维数越高，计算效率提高幅度越大。

为了进一步检验LTEI－EFG法在求解强对流问题时的有效性，取Re＝1000，均匀布置41×41个节点进行计算。图6给出了计算到t＝1.0s时的数值解，图7给出了沿直线y＝0.0处在不同时刻的数值解。由图6和图7可见，对于充分大的Re数，LTEIEFG法仍然能够消除数值伪振荡，其数值解与文献［11－12］的结果一致，且LTEI－EFG法消除伪振荡的效果更好。

图6 t＝1.0s时LTEI－EFG法的数值解Fig.6 Numerical solution of LTEI－EFG method at t＝1.0s（Re＝1000）

图7 不同时刻时沿直线y＝0的数值解Fig.7 Numerical solution along the line y＝0at different time

4 结 论

建立了局部Taylor展开积分无单元Galerkin法，并对一维定常对流扩散方程和二维Burgers方程进行了求解。所得结论如下：

（1）求解流动问题时，LTEI－EFG法的计算效率明显高于采用背景网格积分的EFG方法。

（2）采用直接节点积分的EFG方法求解对流占优问题时会出现数值伪振荡，且比用背景网格积分的EFG方法数值伪振荡更加剧烈。而LTEI－EFG法可以很好地消除由于对流占优引起的数值伪振荡，并且该方法不需要选择稳定化参数。

（3）LTEI－EFG法完全不需要网格，是一种纯无网格方法。

［1］BELYTSCHKO T，LU Y Y，GU L.Element－free galerkin methods［J］.Int.J.Numer.MethodsEng，1994，37：229－256.

［2］LIU G R，GU Y T.An introduction to meshfree methods and their programming［M］.Springer，2005.

［3］李九红，程玉民.无网格方法的研究进展与展望［J］.力学季刊，2006，24：143－152.

［4］张雄，刘岩.无网格法［M］.清华大学出版社，Springer，2004.

［5］欧阳洁，张林，张小华.求解非稳态对流占优问题的非标准无网格Galerkin方法［J］.空气动力学学报，2007，25：287－293.

［6］BEISSEL S，BELYTSCHKO T.Nodal integration of the element－free Galerkin method［J］.Comput.Methods Appl.Mech.Eng.，1996，139：49－74.

［7］NAGASHIMA T.Node－by－node meshless approach and its application to structural analyses［J］.Int.J.Numer.MethodsEng.，1999，46：341－385.

［8］LIU G R，ZHANG G Y，WANG Y Y，et al.A nodal integration technique for meshfree radial point interpolation method（NI－RPIM）［J］.Int.J.SolidsandStructures，2007，44：3840－3860.

［9］DYKA C T，INGEL R P.An approach for tensile instablity in smoothed particle hydrodynamics［J］.ComputStruct.，1994，57：573－580.

［10］CHEN J S，PAN C，WU C T.A Lagrangian reproducing kernel particle method for metal forming analysis［J］.Comput.Mech.，1998，22：289－307.

［11］DONEA J，HUERTA A.Finite element methods for flow problems［M］.Wiley，2003.

［12］ZHANG X H，OUYANG J，ZHANG L.Element－Free Charateristic Galerkin method for Burgers'equation［J］.Eng.Anal.BoundaryElem.，2009，33：356－362.