从一维半无限高方势阱的能级过渡到一维无限深方势阱的能级
2012-09-19郑文礼
郑文礼, 杨 巍
(河北民族师范学院 物理系,河北 承德 067000)
从一维半无限高方势阱的能级过渡到一维无限深方势阱的能级
郑文礼, 杨 巍
(河北民族师范学院 物理系,河北 承德 067000)
先从定态薛定谔方程求解出一维无限深方势阱的能级公式及波函数,再从一维半无限高方势阱的能级图解图导出一维无限深方势阱的能级公式,说明一维无限深方势阱的能级确实是一维半无限高方势阱的能级在特定条件下的极限。最后还对一维半无限高方势阱的能级数目进行了讨论,并给出了相应的判别公式。
一维方势阱;能级;判别公式
引言
求解量子束缚体系的能级是量子力学的重要任务。本文先从定态薛定谔方程求解出一维无限深方势阱的能级及波函数,然后用图解的方法求解出一维半无限高方势阱的能级,采用取极限的方法将一维半无限高方势阱的能级过渡到一维无限深方势阱的能级。这种方法对求解其它形式势阱的能级具有指导作用。
1 一维无限深方势阱的能级[1][2][3][4]
在一维空间中运动的粒子,它的势能在一定的区域内(-a 图1 一维无限深方势阱 这种势称为一维无限深方势阱。在Ι区势能为0,根据定态薛定谔方程可得出Ι区的定态薛定谔方程为又因为体系在一维空间中,所以Ⅰ区的定态薛定谔方程为 而在阱外的Ⅱ区和Ⅲ区的定态薛定谔方程为 (3)式中U0=∞。根据波函数应满足的连续性条件,得出ψI(a)=ψⅡ(a),ψI(-a)=ψⅢ(-a)。 同理(3)式可改写成 (6)式为二阶常系数线性齐次微分方程,其通解是 其中A,B为常量。(7)式的通解为 其中C,D为常量。分区间写成 其中B′,A′,B″,A″均为常量。 由于波函数满足有限性,当x→∞时,ψⅡ应有限,于是B′=0;同理当x→-∞时,A″=0。所以(9)式改写为 (10)式改写为 由于波函数满足连续性,得到ψI(a)=ψⅡ(a)=0,ψI(-a)=ψⅢ(-a)=0。 这是一个二元一次方程组,系数A,B不能全为零的充分必要条件为 即ei2αa-e-i2αa=0,根据欧拉公式,将它展开得则则当n=0时,满足Aeiαa+Be-iαa=0,得到A+ B=0。因为ψ(x)=Aeiαx+Be-iαx,当n=0时,ψ(x)=A+B=0。即当n=0时,对应于ψ恒为零的解,这是平凡解,是无意义的。当n=-1,-2,-3……的解与n等于相应正整数的解线性相关(差一负号),不给出新的解,所以n等于负整数时都不取新的解。将代入 得到 将A=(-1)n+1B代入ψI(x)=Aeiαx+Be-iαx中,当n= 1,3,5,…时,有A=B,于是ψI(x)=A(eiax+e-iax)=2Acosαx=当n=2,4,6…时,A=-B,则 又因为波函数满足归一化条件,而且ψⅡ(x)=ψⅢ(x)=0,则有 一维无限深方势阱中粒子的定态波函数为 图2 一维无限深方势阱能级图 一维半无限高方势阱的势阱图为图3。 图3 一维半无限高方势阱 一维半无限高方势阱的表达式为 因为(16)式与一维无限深方势阱Ι区的方程相同,故在0 对于Ⅱ区,E>U0的散射情况在此不作讨论,仅讨论0 由于波函数的连续性,ψ(x)在x=0处应保持连续,即ψⅢ(0)=ψI(0),得到A+B=0。由于ψ(x)在x=a处作有限跳跃,故ψ(x)在x=a处仍应保持连续,即ψI(a)=ψⅡ(a),Aeiαa+Be-iαa=A′e-λa,由于A+B=0,上述方程化简为 解之,得i2Asinαa=A′e-λa,即 这是一个典型的超越方程,一般只能用图解法给出数值解,而不能用一般的函数关系式表示其解。又因为,同理得则 当α0→∞时,则U0→∞,则半无限高方势阱变为无限深方势阱,P1,P2,P3……分别与……重合,即可推知,pn与重合,相应的 由于这里的势阱宽度为a,如果将a变为2a,即与一维无限深方势阱的宽度相同,则能级公式变为 于是一维半无限高方势阱的能级公式便过渡到了一维无限深方势阱的能级公式。说明一维无限深方势阱是一维半无限高势阱在两边势壁无限高,阱宽相同情况下的特例。 由半无限高方势阱能级图解图可以看出,半无限高方势阱至少存在一个束缚态的条件是α1=α0所以 本文先从定态薛定谔方程求解出一维无限深方势阱的能级公式及波函数,再从一维半无限高方势阱的能级图解图导出一维无限深方势阱的能级公式,说明一维无限深方势阱的能级确实是一维半无限高方势阱的能级在特定条件下的特例。从对一维半无限高方势阱的能级数目讨论的过程中,总结出了相应的能级判别公式。采用本方法可以研究二维甚至是三维势阱的能级。 [1]周世勋,陈灏.量子力学基础[M].高等教育出版社,2009. [2]关洪.量子力学基础[M].高等教育出版社,1999. [3]周世勋.量子力学简明教程[M].高等教育出版社,1979. [4]张慈.量子力学简明教程[M].高等教育出版社,1979. [5]唐启祥.从一维半无限高方势阱的能级过渡到一维无限深方势阱的能级[J].文山师范高等专科学校学报,2002,14(5):69-72. O413.1 A 2095-3763(2012)02-0056-04 2012-02-20 郑文礼(1968-),男,满族,河北平泉人,河北民族师范学院物理系副教授,研究方向为低维半导体结构中电子、激子态。
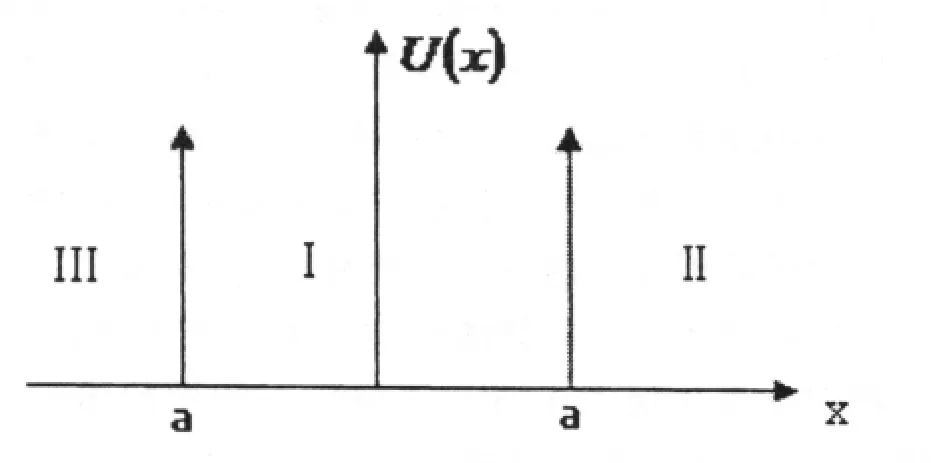

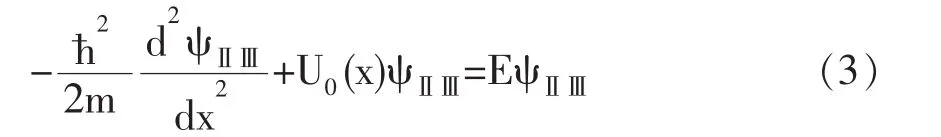

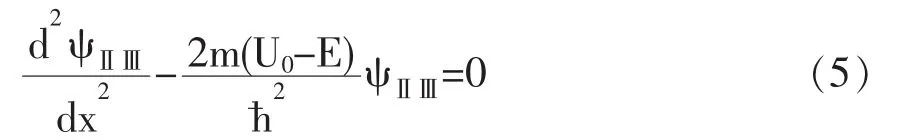


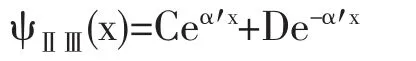


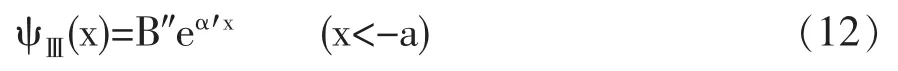
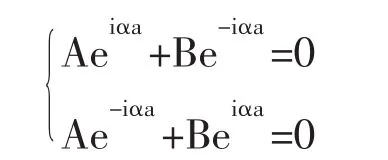



2 一维半无限高方势阱的能级[5]
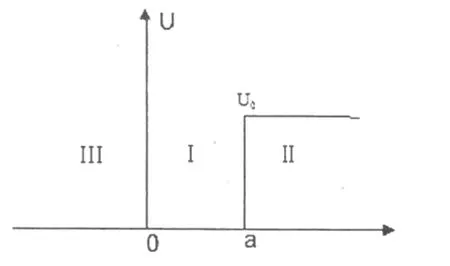
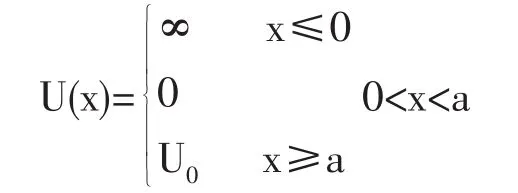









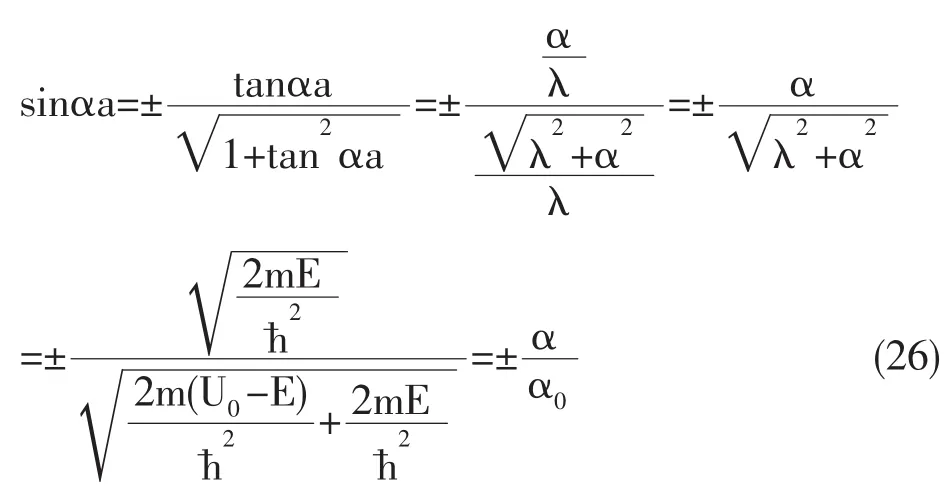
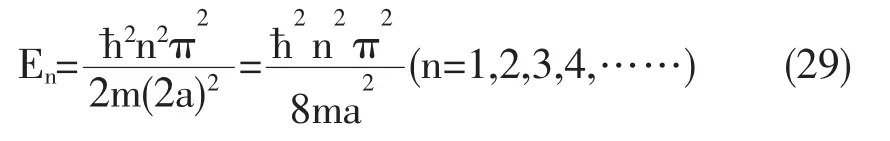
3 讨论

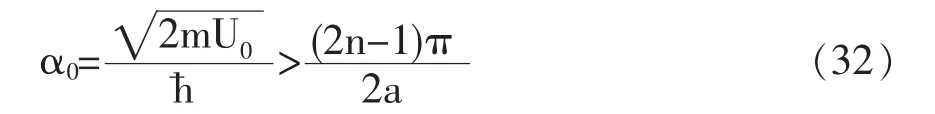
4 总结
