娄和忠，李功胜，贾现正

（山东理工大学理学院应用数学所，山东淄博255091）

近年来，随着计算机技术的发展，利用数值反演确定地下水溶质运移模型中的弥散系数或源项系数等控制参数的方法越来越受到地下水工作者们的重视．苏超伟［1]提出了最佳摄动量算法，并对反应扩散方程扩散系数的识别等参数反演问题进行了数值求解．Li等［2－5]利用最佳摄动量算法对一维溶质运移模型中依赖于空间和时间变化的源项系数进行了反演研究，并与一维土柱实验的实验数据进行拟合，很好地阐释了实验结果．Nie等［6]利用最佳摄动量算法对二维水质模型中的综合扩散系数进行了反演，并与检测数据进行了对比，数值结果表明是合理的．闵涛等［7－10]利用有限差分方法对二维变系数抛物型方程进行了数值计算，并且采用遗传算法，摄动量算法以及拟牛顿算法对模型中的参数进行了反演研究．崔凯等［11]基于同伦映射的思想提出了一种正则参数依赖于迭代次数变化的同伦正则化算法，并利用该算法对一维溶质运移模型中的多个参数进行了反演，数值结果表明了该算法的有效性．越来越多的研究表明利用数值反演的方法确定模型中的未知参数是非常有效地．总体上看，基于同伦思想对参数的反演研究大部分是对于常数形式的模型参数的反演，但当未知参数是随时间或空间变化的函数形式时，同伦算法的有效性还需进一步验证．

1 弥散系数反演问题

本文考虑如下二维对流弥散方程初边值问题：

初始条件

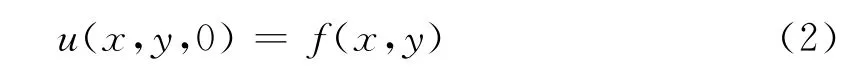
边界条件

其中，Ω＝｛（x，y，t）｜0≤x≤1，0≤y≤1，0≤t≤T｝u（x，y，t）为溶质浓度，DL（x）＞0为纵向弥散系数，DT（y）＞0为横向弥散系数，v＞0为沿x方向的地下水流速．

如果上述初边值问题中的各个参数都已知，利用有限差分方法即可求得其数值解．然而，在实际问题中，弥散系数往往是不可知的．选择观测点x＝x0（这里x0是区域（0，1）内的一点），给定某个终止时刻t＝T时的观测值作为附加数据，即有附加条件

则由（1）－（5）即构成了一个确定弥散系数DL（x）和DT（y）的参数反演问题．

2 同伦正则化算法

同伦正则化算法属于显式迭代算法，通过使用一种正则参数依赖于迭代次数的选取方法，可以避免在迭代过程中由于试探正则化参数带来的无效计算，提高了计算效率．

本文对弥散系数DL和DT的反演采用同伦正则化算法．记D＝（DL，DT），假设和分别是DL（x）和DT（y）所在空间中的一组基，则DL（x）和DT（y）可以取有限项来近似如下

和

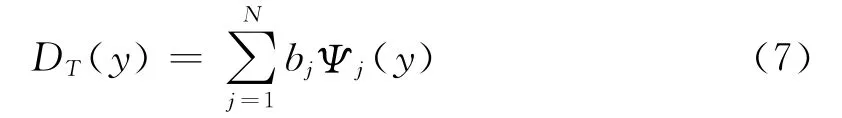
其中，ai（i＝1，2，…，M）和bj（j＝1，2，…，N）是展开项系数．因此，弥散系数在已知基函数的前提下可以写成D＝（a1，a2，…，aM，b1，b2，…，bN）．

给定弥散系数的一个真解D，通过数值方法可求得正问题的数值解，记为u（x，y，t；D）．联系到附加数据θ（y），上述弥散系数的数值反演可以化为一个极小问题的求解

其中α＞0为正则参数．

根据摄动算法的思想，上述极小问题的求解又可以转化为对于给定的初始迭代值DI，求解最佳摄动量δDI，即由如下迭代

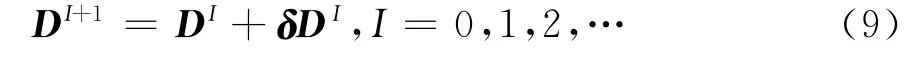
这里δDI是下述泛函的极小解

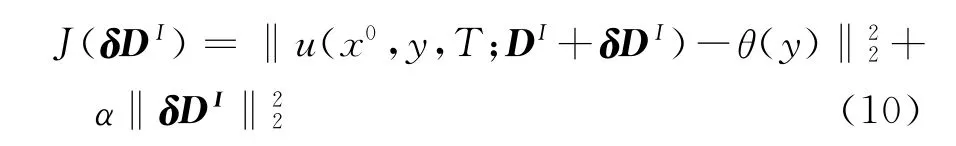
基于同伦算法的思想，对（10）式进行不动点同伦修正，定义新的目标函数如下

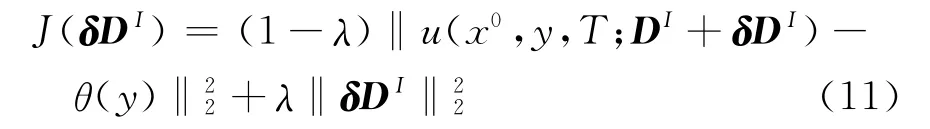
其中，同伦正则参数λ∈（0，1）采用拟神经网络函数定义如下

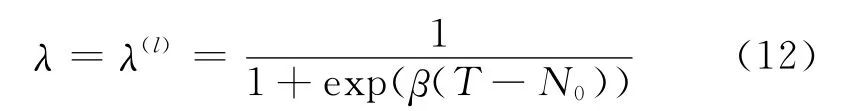
上式中N0为初值选取参数，β为下降速率参数，λ（I）是第I步迭代时正则参数的取值．

图1 同伦正则参数随迭代次数的变化

本文数值反演中取N0＝1，β＝0．5．图1给出了同伦正则参数随迭代次数的变化图像．

注意到上式中的δDI是一个微小的扰动量，将u（x0，y，T；DI＋δDI）在DI处利用多元泰勒公式展开得

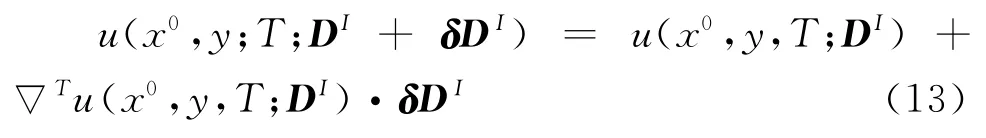
若对于（x0，y，T）有Q个离散点（x0，yq，T）（q＝1，2，…，Q），并且取定‖δDI＝，则得

容易验证［8]，上述泛函极小问题的求解等价于求解以下规范方程

式中

E为单位矩阵．

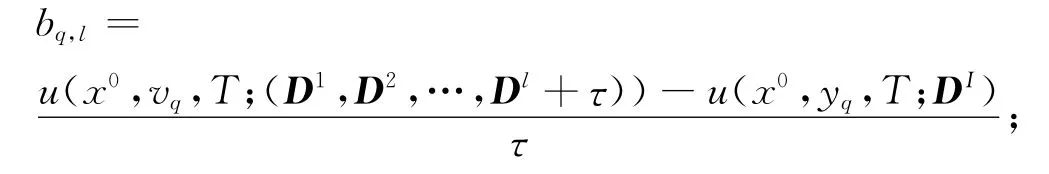
其中τ为数值微分步长，

下面给出同伦正则化算法的实施步骤：

步骤1 给定初始迭代向量D0，τ，求解向量η，ξ以及矩阵B；

步骤2 根据同伦正则化算法求解δDn得到

步骤3 给定收敛精度eps，判断是否满足‖δDI‖≤eps．若满足，则迭代结束．否则转到式（9）继续迭代，直到满足收敛精度为止．

3 数值模拟

利用上述介绍的同伦正则化算法对弥散系数DL和DT进行数值反演．初边值问题（1）－（4）中取定初始值

边界条件

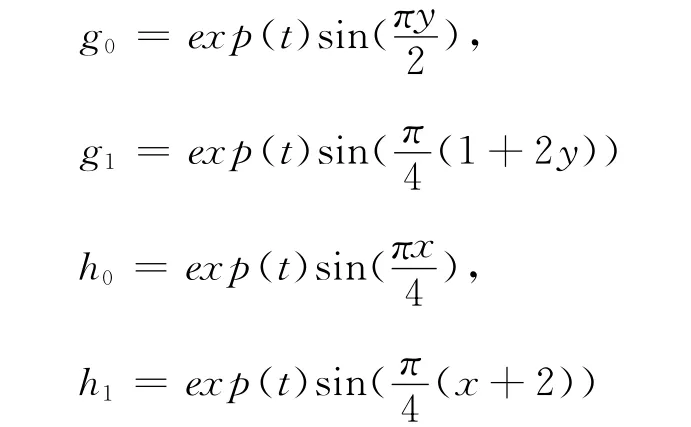
附加数据取终止时刻T＝2时x0＝0．5处的观测值．

下面，在式（6）和式（7）中取M＝N＝3，则纵向弥散系数与横向弥散系数可以近似表示为

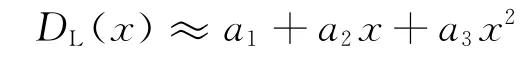
及

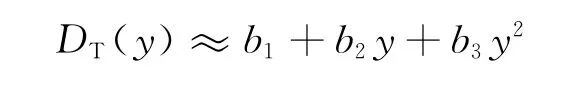
因此，反演参数可简记为

假设DL（x）＝1＋（y）＝1＋＝1．则反演参数的真值Dtrue＝（1，0，1，1，0，0．5）．下面应用同伦正则化算法对此弥散系数进行反演重建．

（1）初始迭代值对反演结果的影响

取数值微分步长τ＝1e－3，迭代收敛精度eps＝1e－6，讨论初始迭代值对算法的影响，计算结果见表1，其中Dinv表示反演解，I表示迭代次数，Err＝‖Dinv－Dtrue表示真解与反演解间的相对误差．

表1 初始迭代值对反演结果的影响

由表1可知，同伦正则化算法对初始迭代值的依赖不是很严格．然而，初始迭代值与真解的距离不能太大，否则，算法将失效．

（2）数值微分步长对反演结果的影响

取初始迭代值D0＝（0．5，0．5，0．5，0．5，0．5，0．5），迭代收敛精度eps＝le－6，讨论微分步长对算法的影响，计算结果见表2．

由表2可知，数值微分步长对算法的实现有一定的影响，微分步长的取值不能太小，不然，算法将不能实现．

（3）收敛精度对反演结果的影响

取初始迭代值D0＝（0．6，0．6，0．6，0．6，0．6，0．6），数值微分步长τ＝1e－3，讨论收敛精度对算法的影响，计算结果见表3．

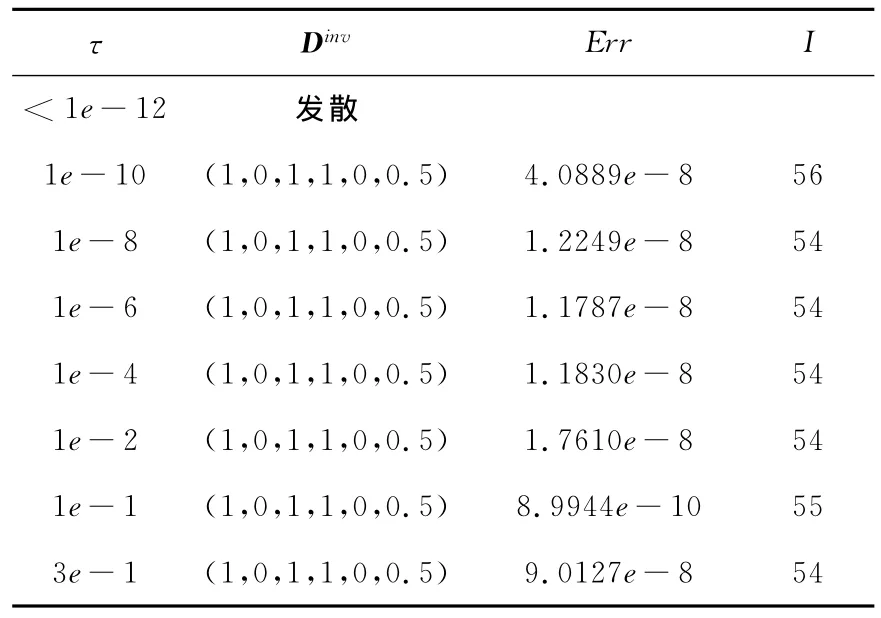
表2 数值微分步长对反演结果的影响

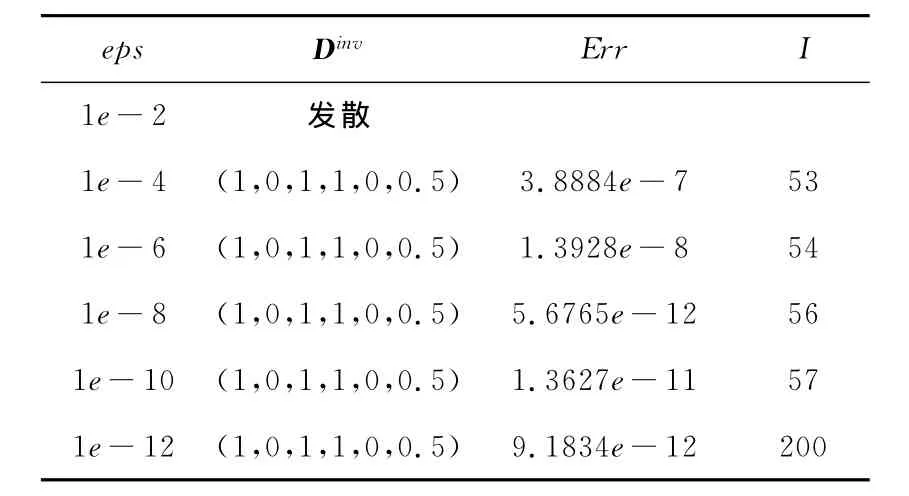
表3 收敛精度对反演结果的影响

由表3可知，收敛精度对算法的影响很大，收敛精度的取值不能太小．随着收敛精度的减小，绝对误差也逐渐变小．但是，收敛精度的取值也不需要太小，否则会影响反演效率．图1和图2分别给出了数值微分步长τ＝1e－3，初始值D0＝（0．1，0．1，0．1，0．1，0．1，0．1）时，纵向弥散系数DL（x）和横向弥散系数DT（y）精确解与反演解得图像比较．

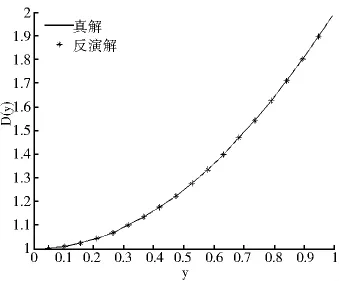
图2 DL（x）＝1＋x2时精确解与反演解的比较

4 结束语

图3 DT（y）＝时精确解与反演解的比较

本文基于同伦正则化算法对二维对流－弥散方程中随时间变化的纵向弥散系数和横向弥散系数进行了反演计算，研究表明了该算法对于此类反问题参数反演的有效性．数值结果表明，数值微分步长对反演算法的影响较小；初始迭代值对算法的影响较大，当初始迭代值与精确解的距离较大时，算法容易失效；收敛精度的取值对算法的实现主要是在于对误差的影响，收敛精度取的太小反而会降低计算效率．

［1] 苏超伟．偏微分方程逆问题的数值方法及应用［M] ．西安：西北工业大学出版社，1995

［2] Li G S，Cheng J，Yao D，et al．One－dimensional equilibrium model and source parameter determination for soil－column experiment［J] ．Applied Mathematics and Computation 2007，190（2）：1 365－1 374．

［3] 李功胜，姚德，马昱，等．一维溶质运移源（汇）项系数反演的迭代正则化算法［J] ．地球物理学报，2008，51（2）：582－588．

［4] Li G S，Liu J Q，Fan X P，et al．A new gradient regularization algorithm for source term inversion in 1Dsolute transportation with final observations［J] ．Applied Mathematics and Computation 2008，196（2）：646－660．

［5] Li G S，Yao D，Jiang H Yet al．Numerical inversion of a time－dependent reaction coefficient in a soil－column infiltrating experiment［J] ．CMES 2011，74（2）：83－107．

［6] Nie N T，Tao J H．Inversion of dispersion coefficient in water quality model using optimal perturbation algorithm［J] ．Applied Mathematics and Mechanics 2009，30（6）：703－712．

［7] 闵涛，张海燕，周宏宇．二维变系数热传导方程初边值问题的交替方向隐格式［J] ．西安工业大学学报，2007，27（2）：199－204．

［8] 闵涛，张世梅，邹学文．二维抛物型方程参数反演的遗传算法［J] ．数学杂志，2007，27（3）：348－352．

［9] 闵涛，卢宏鹏，杨晓莉，等．二维变系数抛物型方程参数反演的摄动量算法［J] ．科技通讯，2010，26（2）：282－287．

［10] 闵涛，卢宏鹏，武苗．二维抛物型方程参数反演模型的拟牛顿法［J] ．计算机工程与应用，2010，46（18）：40－42．

［11] 崔凯，李兴斯，李宝元．求解非线性反问题的大范围收敛梯度正则化算法［J] ．计算力学学报，2005，22（4）：415－419．