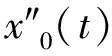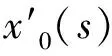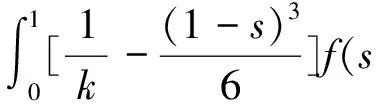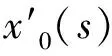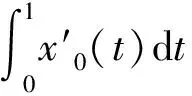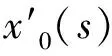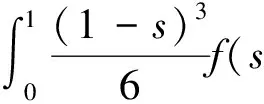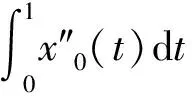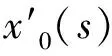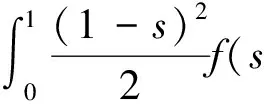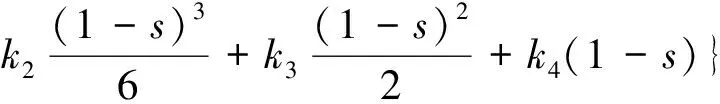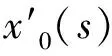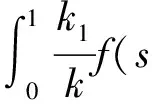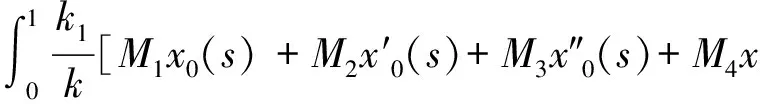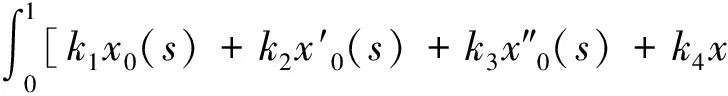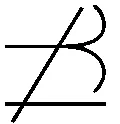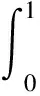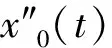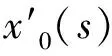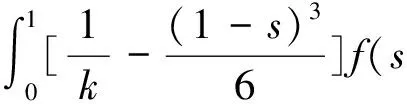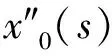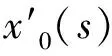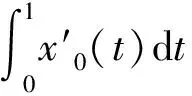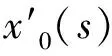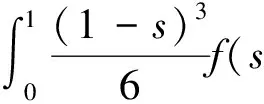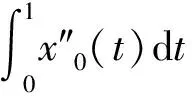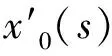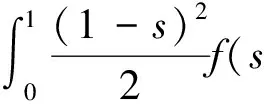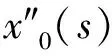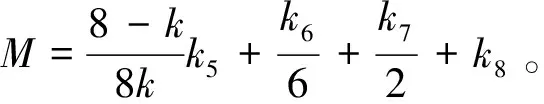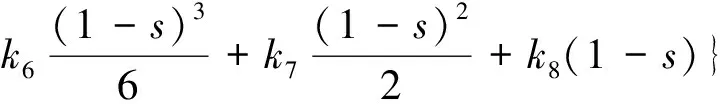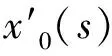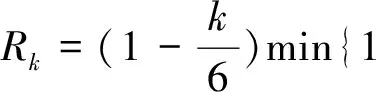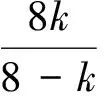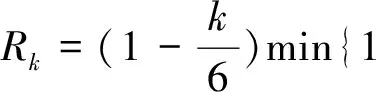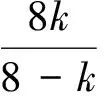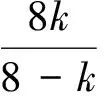一类四阶边值问题的正解的存在性与多重性*
2012-05-09王云杰
王云杰,朱 江
(1.徐州师范大学科文学院, 江苏 徐州 221116;2.徐州师范大学数学科学学院,江苏 徐州 221116)
近年来各种边界条件下的四阶非线性方程边值问题的研究,受到相关人员的普遍关注[1-6]。在文[1]中,张建国等利用范数形式的锥拉伸与锥压缩不动点定理给出了四阶边值问题:
(1)
正解的存在性及多重性。其中,f:[0,+∞)→[0,+∞)连续。
本文考虑了更一般的方程
(2)
其中,f:[0,1]×R4→[0,+∞)连续。首先,我们在Banach空间C3[0,1]中构造了一个锥,然后利用序形式锥拉伸与锥压缩不动点定理,得到了该空间中四阶边值问题(2)一个和多个正解的存在性。
1 预备知识
由文[1]知,四阶边值问题
的Green函数为
G(t,s)=

并有以下结论:
1)在有界闭区域D={(t,s)|0≤t≤1,0≤s≤1}上,当0

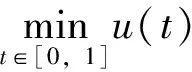
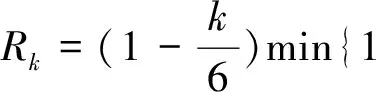
为了证明主要结论, 我们先证明下面几个引理。
引理1 若u∈P,则‖u‖=max{u(1),u‴(1)}。
证明由u‴(0)=0,u‴(t)递增知u‴(t)≥0且u‴(1)=|u‴|0,又由u′(0)=u″(0)=0得
u″(t)≥0,u′(t)≥0
及


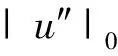
从而
‖u‖=max{u(1),u‴(1)}
引理2P是E中的锥。
证明设{xn}⊂P,xn→x。则易知
x(0)≥0,x′(0)=x″(0)=x‴(0)=0,

当0≤t1≤t2≤1时,有

故x‴(t)递增。又
≥,
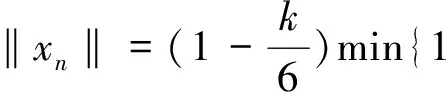
所以x∈P,说明P是E闭集。下再证P是凸集。
事实上,若x1∈P,x2∈P,∀λ∈[0,1]。则
λx1+(1-λ)x2≥0,
(λx1+(1-λ)x2)′(0)=

(λx1+(1-λ)x2)″(0)=
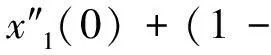
(λx1+(1-λ)x2)‴(0)=
λx‴1(0)+(1-λ)x‴2(0)=0,
k(λx1+(1-λ)x2)(1)=
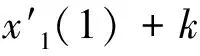
λx‴1(1)+(1-λ)x‴2(1)=
(λx1+(1-λ)x2)‴(1)
且(λx1+(1-λ)x2)‴(t)=λx‴1(t)+(1-λ)x‴2(t)递增。
又当0 (λx1+(1-λ)x2)(t)=λx1(t)+(1-λ)x2(t)≥ 当1 (λx1+(1-λ)x2)(t)=λx1(t)+(1-λ)x2(t)≥ 故有 λx1+(1-λ)x2)(t)≥ 所以λx1+(1-λ)x2∈P。说明P是E中凸集。 显然,若x∈P,λ≥0,则λx∈P;若x∈P,-x∈P,有x=θ。这说明P是E中的一个锥。 由引理 2,可在E中定义由P导出的半序:。即xy⟺y-x∈P。易知,若xy, 则x≤y,y′(0)-x′(0)=y″(0)-x″(0)=y‴(0)-x‴(0)=0,y‴(t)-x‴(t)递增,从而x≤y,x′≤y′,x″≤y″,x‴≤y‴。 定义算子A为 则易知u是BVP(2)的解当且仅当u是A的不动点。由f的连续性容易证明A:P→P是全连续算子。 为了证明本文的主要结果,我们还需要下面的引理。 或 (ii)Axx,∀x∈P∩∂Ω1;Axx,∀x∈P∩∂Ω2; (i)f(s,x,y,z,w)>M1x+M2y+M3z+M4w,其中M1≥k,M2≥k,M3>0,M4>0,(s,x,y,z,w)∈[0,1]×[Rka,a]×[0,∞)×[0,∞)×[0,∞); 证明设Ωa={x∈E|‖x‖ 首先,若x∈∂Ωa∩P,则xAx。 (用反证法)假设∃x0∈∂Ωa∩P,使得x0Ax0。由x0∈∂Ωa∩P,知x0(t)≥Rka。又x0Ax0,故 x0(t)≥Ax0(t)= x‴0(t)≥(Ax0)‴(t)= 两边从0到1积分得 ‴0(t)]dt≥ 矛盾。 (用反证法)假设∃x0∈∂Ωb∩P,使得x0Ax0。由x0∈∂Ωb∩P,知x0(t)≥Rkb。又x0Ax0, 故 x0(t)≤Ax0(t)= x‴0(t)≤(Ax0)‴(t)= 两边从0到1积分得 ‴0(t)]dt≤ 矛盾。 由引理4 (i)得A在P中有不动点。即四阶边值问题(2)有解u∈C3[0,1]且u>0。 利用引理4 (ii),与定理1的证明类似, 可得以下结论。 (ii)f(s,x,y,z,w)>M5x+M6y+M7z+M8w,其中M5≥k,M6≥k,M7>0,M8>0,(s,x,y,z,w)∈[0,1]×[Rkb,b]×[0,∞)×[0,∞)×[0,∞);则四阶边值问题(2)在C3[0,1]至少有一个正解。 将定理1与定理2结合,即得多解的存在性。 (ii)f(s,x,y,z,w)>M5x+M6y+M7z+M8w,其中M5≥k,M6≥k,M7>0,M8>0,(s,x,y,z,w)∈[0,1]×[Rkb,b]×[0,∞)×[0,∞)×[0,∞); 则四阶边值问题(2)在C3[0,1]至少有两个正解。 参考文献: [1]张建国,张福伟,刘进生.一类四阶方程边值问题正解的存在性与多重性[J].工程数学学报,2005,22(5): 864-868. [2]吕志伟,华守亮,杨辉.Banach空间中一类四阶奇异边值问题的解的存在性[J].数学的实践与认识, 2008,38(24): 195-199. [3]姚庆六.一类含参数半正四阶边值问题的正解存在性与多解性[J].数学学报,2008,51 (2): 401-410. [4]柴国庆.四阶奇异边值问题的正解[J].数学物理学报,2005,25A(6): 898-904. [5]韦忠礼.四阶奇异边值问题的正解[J].数学学报,1999,42(4): 715-722. [6]席莉静.四阶奇异边值问题正解的存在性与多重性[J].应用泛函分析学报,2005,7(1): 46-50. [7]郭大钧.非线性泛函分析[M].济南:山东科技出版社,1985. [8]郭大钧.非线性分析中的半序方法[M].济南:山东科技出版社,2000. [9]郭大钧,孙经先.抽象空间常微分方程[M].济南:山东科技出版社,1988. [10]郭大钧,孙经先,刘兆理.非线性常微分方程泛函方法[M].济南:山东科技出版社,2005.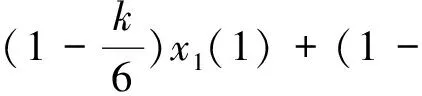
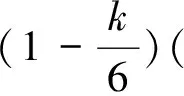
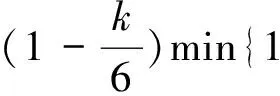
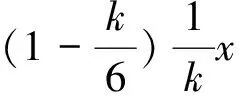
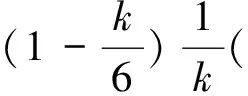
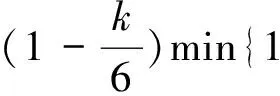
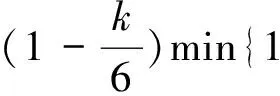
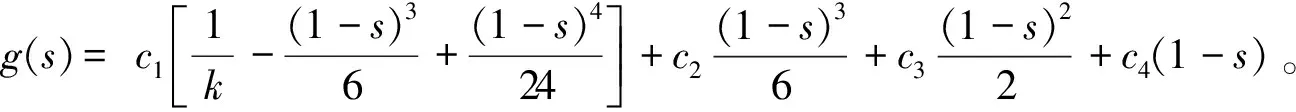
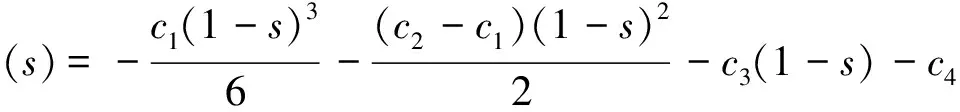

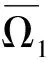
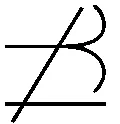
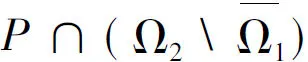
2 主要结果