焦 佳，高 洋，周庆健

(大连民族学院理学院，辽宁大连 116605)

微分方程系统不可积性问题研究

焦 佳，高 洋，周庆健

(大连民族学院理学院，辽宁大连 116605)

研究了周期系统Laurent多项式型首次积分和有理首次积分的不存在性问题。利用Floquet理论，证明了如果系统的特征乘数是ℤ －非共振的，则系统在平衡点附近不存在Laurent多项式型首次积分。进一步，还在有理函数空间考虑了这一问题，并得到了相应的结果。

Floquet理论;Laurent多项式型首次积分;形式首次积分;有理首次积分

1 自治系统

在物理、力学、化学、生物、工程等领域的各种动态数学模型，往往归结为非线性微分方程。这些方程可分为两大类:可积的与不可积的。一般说来，随着时间的变化，可积系统总是呈现出有规律的可预测的行为;而在很多情况下，不可积系统在其相空间的某区域上的运动是无规律的和混沌的。长期以来，由于解方程的需要，可积性问题已变成数学和物理学家所关心的基本问题之一，并得到了很多重要的结果。近些年来，随着人们对混沌现象越来越感兴趣，对不可积系统的研究也越来越多。

考虑如下解析系统

式中，x=(x1，…，xn)∈ℂn，f(x)=(f1(x)，…，fn(x))。

定义1 单值函数Φ(x)称为系统(1)的一个首次积分，如果Φ(x)沿着系统(1)的任何一条解曲线都是常数。若Φ(x)是可微的，则可将其写为

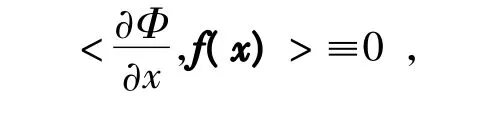
式中，＜.，.＞表示欧式空间的内积。

对于给定的系统(1)，在什么样的条件下系统具有首次积分?除了某些简单的情形，这个问题是非常困难的，并且迄今尚无一种办法能对一给定的系统构造出首次积分，因此证明系统的可积性是非常困难的。这样，迫使人们不得不换一个角度来证明系统的不可积性，即:如果系统(1)(在某个函数空间)不存在任何首次积分，则称系统(1)(在此函数空间上)是不可积的。

注1detA≠0，这个条件是可以去掉的。因为事实上，不满足共振条件(3)已经保证了这个条件。

定义2设K是给定的数域，αi∈K，{b1，…，bk}是复向量空间E的一个有限子集，如果α1b1+α2b2+… +αkbk=0蕴含 α1=α2=… =αk=0，则称b1，…，bk是K －独立的。

近年来，众多学者都开始关注这方面的问题，先后在解析函数、有理函数、多项式和Laurent多项式等函数空间，对一般非线性系统、拟齐次系统和半拟齐次系统给出了不存在首次积分的判别准则。

1983 年，Yoshida［2］利用奇性分析法，根据Kovalevskaya指数［3］(以下简称 K － 指数)给出了一类尺度不变系统代数可积的必要条件。

定理2如果系统(1)是弱代数可积的，那么所有K－指数都是有理的。

这个结果虽然在当时被人们广泛地应用，但是在1991 年，Kummercite［4］对于这个定理给出了一个反例。进而，人们对这个定理进行了修正，得到了如下修正后的Yoshida定理［2］。

定理3如果系统(1)是代数可积的，那么所有K－指数都是有理的。也就是说，如果至少有一个K－指数是无理数或虚数，那么系统不是代数可积的。

随后，人们在不同的函数空间也考虑了这个结果［5－6］。

定理4如果存在一个平衡ξ使K－矩阵是半单的，且K－指数 ρ1，…，ρn是ℤ －独立的(ℕ －

那么系统(1)没有任何非平凡的多项式首次积分。进一步，如果系统(1)是正半拟齐次的，那么在x=0附近不存在任何非平凡的形式首次积分。

1996 年，Nowicki［8］利用微分代数理论，对线性系统

给出了存在形式首次积分和有理首次积分的必要条件。

定理6设线性系统(2)的矩阵A是半单的。如果特征值λ1，…，λn是ℕ －独立的，那么当且仅当系统(2)没有任何非平凡的形式首次积分。另外，如果特征值是独立的，那么当且仅当系统(2)没有任何非平凡的有理首次积分。

注2这里称矩阵A半单是指矩阵A是可对角化的。

2003年以来，史少云先后给出了一般非线性系统和半拟齐次系统不存在Laurent多项式首次积分和有理首次积分的判定准则，见文献［9－10］。

例1 考虑如下广义的二维Volterra－Lotka系统第一种判别法:

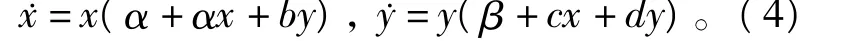
由定理1可知，如果对任意k1，k2∈ℕ∪{0}，k1+k2≥1，独立的)，那么不存在有理(多项式)首次积分。

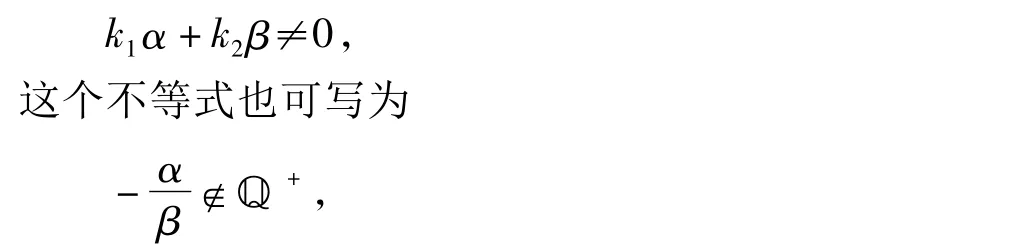
受到 Yoshida 工作的启发，1996 年，Furta［7］研究了半拟齐次系统的不可积性，利用K－指数给出了半拟齐次系统不存在解析首次积分的判定准则。

定理5设系统(1)是半拟齐次系统，如果其拟齐次截断系统的K－矩阵是对角的，且它的特征值λ1，…，λn不满足任何共振等式

那么系统(4)在x=y=0附近没有任何非平凡的解析首次积分。

第二种判别法:

系统(4)是负半拟齐次系统，在指数sx=sy=1下有二阶拟齐次截断，

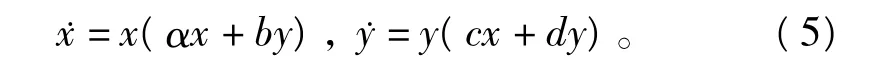
如果ad－bc≠0，则系统(5)有如下形式的特解:根据定理5，如果

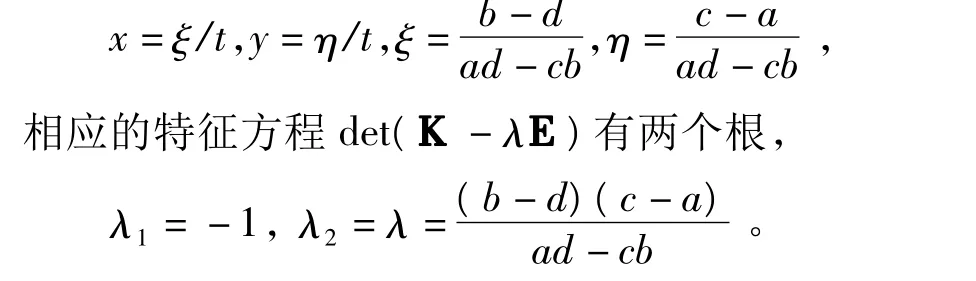
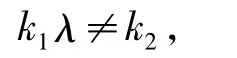
那么系统(4)没有非平凡的多项式首次积分。此不等式还可写为

2 非自治周期系统

考虑如下周期系统

其中(t，y)∈S1× ℂn(S1= ℝ /ℕ T)，且f(t+T，y)=f(t，y)。设y=0是系统的平衡点，即对所有的 t∈S1都有f(t，0)=0。可将系统(6)重写为

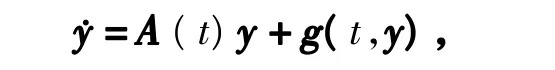
式中，A(t+T)=A(t)，g(t，y)是关于y 的展开式中所有高于一次的项的总和，且满足g(t+T，y)=g(t，y)。

定义3 称单值函数Φ(t，y)为周期系统(6)的首次积分，若Φ(t，y)关于t是T－周期函数且沿着系统(6)的任何一条解曲线都是常数。如果Φ(t，y)是可微的，则可将其写为

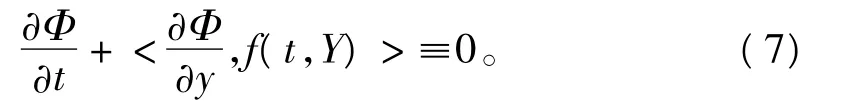
如果Φ(t，y)可展开成关于y的形式幂级数(有理函数)且满足式(7)，那么称 Φ(t，y)系统(6)的形式(有理)首次积分。

注3 我们还考虑了系统(6)的Laurent多项式型首次积分，这里，Laurent多项式是指

式中，Φk1，…，kn(t)是关于 t的函数，A 是整数集ℤn的一个有限子集。如果Φ(t，y)关于t是T－周期的可微函数，且满足式(7)，那么称函数Φ(t，y)是系统(6)的Laurent多项式型首次积分。

根据定义，常值函数显然是系统(6)的首次积分，称为平凡积分。本文中所说积分都是指非平凡的。

那么系统(6)在y=0附近不存在任何非平凡的形式首次积分。

我们主要给出了这个定理的一个新的证明［13］且考虑了系统(6)Laurent多项式型首次积分的不存在性［14］，并进一步在有理函数空间考虑了此结果［15］，得到如下定理:

定理8设y=0是系统(6)的平衡点，若系统(6)的特征乘数是ℤ －非共振的，即不满足任何共振条件

由Floquet理论［11］知，存在周期为 T的矩阵函数B(t)，使得在线性变换

下，系统(6)变为

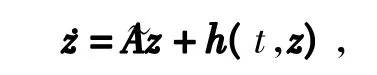
式中，~A是一个常数矩阵;h(t，z)是关于z的展开式中所有高于一次的项的总和，且满足h(t+T，z)=h(t，z)。矩阵~A的特征值λi称为系统

的特征函数，矩阵eT~A的特征值μi=eλiT称为式(8)的特征乘数。

2003年，李伟顾等人［12］研究了微分同胚和如上周期系统(6)形式首次积分的不存在性。

定理7设y=0是系统(6)的平衡点，如果系统(8)的特征乘数不满足任何共振条件:

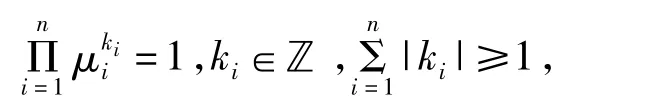
那么系统(6)在平衡点附近没有任何非平凡的Laurent多项式型首次积分。

定理9设y=0是系统(6)的平衡点，且μ1，…，μn是线性系统(8)的特征乘数，如果系统(6)在平衡点y=0附近有一个非平凡有理首次积分，则存在非零整数向量k=(k1，…，kn)∈ℤn使得的基本解矩阵为

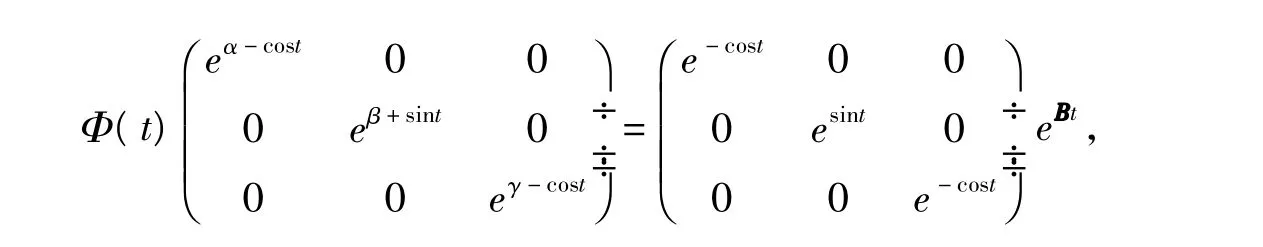
根据定理9，周期系统(9)在平衡点附近没有任何非平凡的有理首次积分。

3 结语

介绍了解析系统不可积性的一些判定准则。针对已有结果大多考虑的是自治系统，而对于非自治的周期系统研究的还很少，这里给出了非自治周期系统不存在Laurent多项式型首次积分和有理首次积分的充分条件。

［1］ POINCARÉ H. SurI ＇intégrationsdes équations fifférentielles du premier order et dupremier degré I and II Rend［J］.Circolo Mat Palermo，1891，11:193 －239.

［2］YOSHIDA H.Necessary condition for the non － existence of algebraic first integral(Ⅰ，Ⅱ) ［J］.Celestial Mech，1983，31:363－379，381－399.

［3］KOWALEVSKI S.Sur le probleme de la rotation d＇un corps solide autour d＇un point fixe ［J］.Acta Math.，1889，12:177－232.

［4］KUMMER M，CHURCHILL R C，ROD D L.On Kovalevski expoenents［J］.Can.Math.Bull.，1990，33:175－180.

［5］ GORIELY A.Integrability，partial integrability，and nonintegrability for systems of ordinary differential equations［J］.J.Math.Phys.，1996，37:1871 －1993.

［6］SADETOV S T.On resonances of the Kovalevskaya exponents［J］.Math.Notes，1993，54:1081 －1083.

［7］FURTA S D.On non－integrability of general systems of differential equations［J］.Z Angew Math Phys，1996，47:112－31.

［8］NOWICKI A.On the nonexistence of rational first integrals for systems of linear differential equations［J］.Linear Algebra Appl，1996，235:107 －120.

［9］SHI Shaoyun，LI Yong.Non－integrability for general nonlinear systems［J］.Z Angew Math Phys，2001，52:191－200.

［10］SHI Shaoyun.On the nonexistence of rational first integrals for nonlinear systems and semiquasihomogeneous systems［J］.J.Math.Anal.Appl.，2007，335:125－134.

［11］CHICONE C C.Ordinary Differential Equationas with Applications［M］.New York:Springer－ Verlag，1999.

［12］LI Weigu，LLIBRE J，ZHANG Xiang.Local first integrals of differential systems and diffeomorphisms［J］.Z Angew Math Phys，2003，54:235 －255.

［13］JIAO Jia，SHI Shaoyun，XU Zhiguo.Formal first integrals for periodic systems［J］.J.Math.Anal.Appl.，2010，366:128－136.

［14］焦佳，付苗苗，马勇.周期系统Laurent多项式型首次积分的不存在性［J］.吉林大学学报:理学版，2009，47:44－47.

［15］JIAO Jia，SHI Shaoyun，ZHOU Qingjian.Rational first integrals for periodic systems［J］.Z Angew Math Phys，2011，62:233 －243.

Non－integrability of Differential Equation Systems

JIAO Jia，GAO Yang，ZHOU Qing－jian

(College of Science，Dalian Nationalities University，Dalian Liaoning 116605，China)

The nonexistence of the first integrals of Laurent polynomial and the rational first integrals for periodic systems are considered.Using the Floquet theory，that if the characteristic multipliers of the system are ℤ － dependent，then the system does not have any nontrivial integral of Laurent polynomial in a neighborhood of a constant solution is proved.Furthermore，the previous conclusion in the rational function space is also considered.

Floquet theory;Laurent polynomial first integral;formal first integral;rational first integral

O175

A

1009－315X(2011)05－0472－04

2011－05－25;最后

2011－06－16

国家自然科学基金资助项目(10872045);大连民族学院博士启动基金资助项目(20096209)。

焦佳(1982－)，女，河南焦作人，讲师，博士，主要从事非线性常微分方程研究。

(责任编辑 邹永红)