王艳芳

(大连大学信息工程学院，中国 大连 116622)

一个多处理器系统中实现处理器间通信的互连网络通常以有向或无向图作其数学模型．近年来，通过一些有限群来构造的Cayley图为模型已经成为设计网络的主要方法之一[1]．上世纪80年代提出的Star网络就是Cayley网络的一个范例[1-2]．具有Hamilton圈的图称为Hamiltonian的，Hamiltonian是互连网络的一个基本网络性质，它为设计网络算法提供一个直观的路径．

1985年B.Alspach提出如下猜想[3]：如果Abel群上F上连通的Cayley图G(F，S)的度为2K，那么G(F，S)是K个边互不相交的Hamilton圈的并；如果G(F，S)的度为2K+1,那么G(F，S)是K个边互不相交的Hamilton圈和一个1-因子的并.J.C.Bermonel证明了，如果G(F，S)的度为4[4]．那么G(F，S)可分解为两个边互不相交的Hamilton圈的并.王殿军等证明了T是F的极小生成元集时(G(F，TUT-1)是Abel群上连通Cayley图，且TUT-1只含二阶元)猜想成立[5]．对于交换群上6度Cayley图的Hamilton圈分解，正如J.C.Bermonel在[4]中指出的“一般情况下是很难的”目前只对笛卡尔积的情况给出了证明．文献[6]中证明了阶为奇数交换群上Cayley图X=Cay(G，S)，当S为G的极小生成集时，猜想成立．本文利用“Hamilton圈上侧枝循环法”给出了阶为偶数交换群上6度Cayley图的Hamilton圈一般性分解方案和理论证明．

1 预备知识

关于“H方与H方操作”，“Hamilton圈上单向通道”，“Q特性”的定义和“离合法”见文献[7].

设G=〈 a，b，c | ak=1，aβ=bα，aβ=cα，ab=ba，ac=ca，bc=cb〉的Cayley图为X=Cay(G，S)，(S={a±1，b±1，c±1})，在X=Cay(G，S)，(S={a±1，b±1，c±1})中，令La，t，h=(btch，abtch，a2btch，…，ak-1btch，btch)，t，h=0，1，2，…α-1；Lb，t，h=(atch，atbch，atb2ch，atb3ch，…，atbλx-1ch，atch)，t=0，1，2，…，β-1，h=0，1，2，…，α-1；Lc，t，h=(atbh，atbhc，atbhc2，atbhc3，…，atbhcλx-1，atbh)，t=0，1，2，…，β-1，h=0，1，2，…，α-1，λ=k/β，bλα= cλα=1；

Wa,i=La,o,i∪La,1,i∪La,2,i∪，…，∪La,α-1,i(i=0，1，2，…，α-1)；

Wb,i=Lb,o,i∪Lb,1,i∪Lb,2,i∪，…，∪Lb,β-1,i(i=0，1，2，…，α-1)；

Wc,i=Lc,o,i∪Lc,1,i∪Lc,2,i∪，…，∪Lc,β-1,i(i=0，1，2，…，α-1)；

令Ca=Wa,0∪Wa,1∪Wa,2∪，…，∪Wa,α-1和Cb=Wb,0∪Wb,1∪，…，∪Wb,α-1及Cc=Wc,0∪Wc,1∪，…，∪Wc,α-1，显然，Ca,Cb,Cc均为X=Cay(G，S)(S={a±1，b±1，c±1})的二因子．

在X=Cay(G，S)(S={a±1，b±1，c±1})中有如下H方

Hi,j,h=(aibjch,aibj+1ch,ai+1bj+1ch,ai+1bjch,aibjch)，

i=0，1，2，…，k-1，j=0，1，2，…，α-1，h=0，1，2，…，α-1.

引理1[7]设两个闭圈C1=(e1，e2，…，em，e1)，C2=(d1，d2，…，dm，d1).若C1和C2间有H方(et，dt，dt+1，et+1，et)，则对此H方进行H方操作后，可使得C1和C2形成一个新的闭圈O=(e1，e2，…，et，dt，dt-1，dt-2，…，d1，dm，dm-1，…，dt+1，et+1，et+2，…，em，e1)，且O通过C1和C2顶点洽好一次．

例1图1是群G=〈a，b，c| a6=1，a3=b4，a3=c4,ac=ca,bc=cb,ab=ba〉 的Cayley图X=Cay(G，S)(S={a±1，b±1，c±1})的Hamilton圈分解图．(X=C1∪ C2∪ C3，C1，C2，C3为X=Cay(G2，S)的3个边互不相交的Hamilton圈)，它是经过对以下H方进行操作得到的:

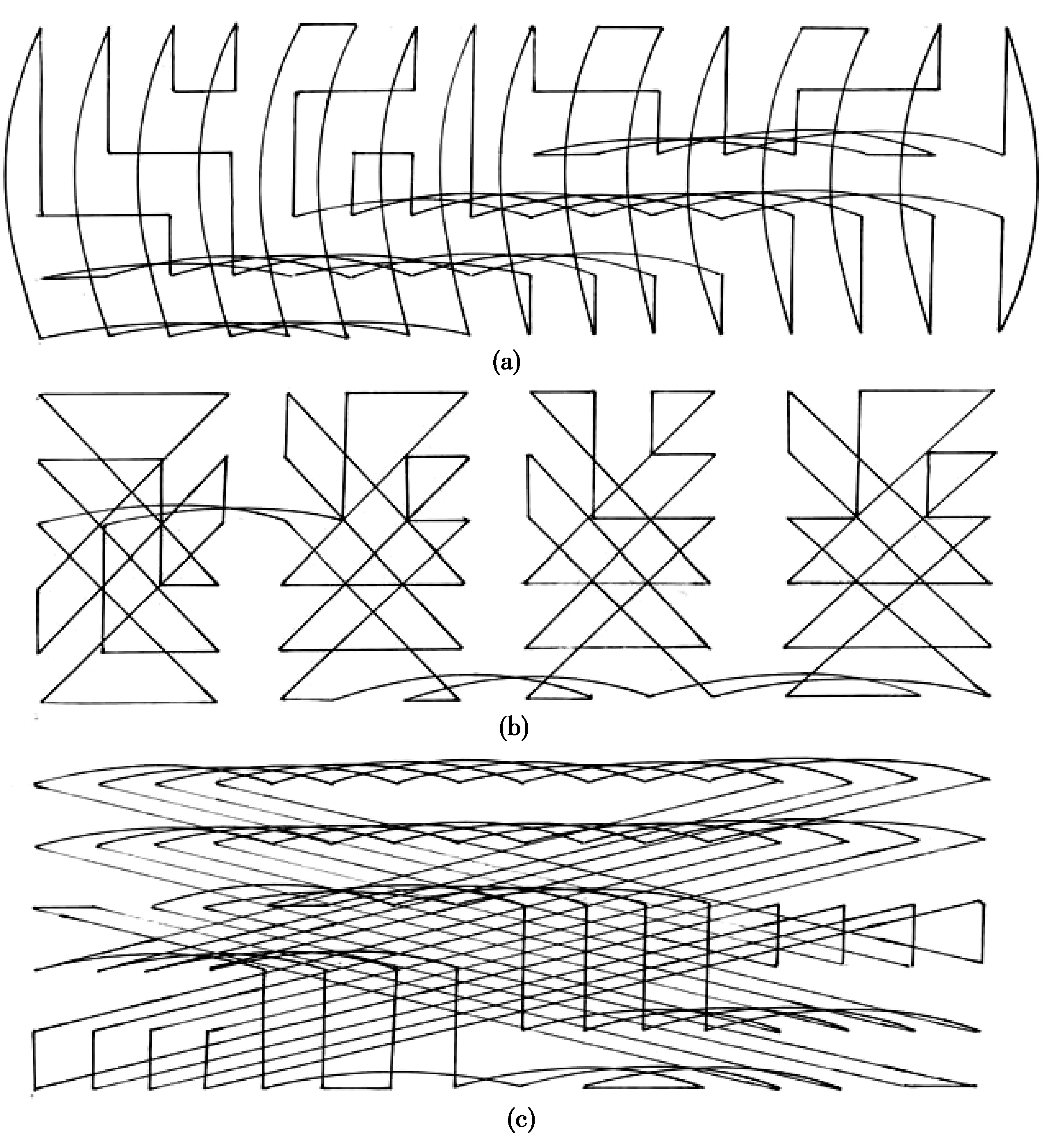
图1 Hamilton圈分解

图2 Hamilton圈分解

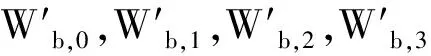
2 6度Cayley 图Hamilton 图分解

对6度Cayley图Hamilton圈分解分不同情况进行，本部分先对当β等于奇数时Γ(β.α.α)型和Γ(β.β.α)型Cayley图的Hamilton圈进行分解和理论证明．

1) 设X=Cay(G1，S)(S={a±1，b±1，c±1})是群G=〈a,b,c | a2β=1,aβ=bα，aβ=cα,ab=ba，ac=ca，bc=cb〉(β为奇数，α为偶数，α>β)的Cayley图，在X=Cay(G1,S)中进行如下操作，可将其分解为3个Hamilton圈C1，C2，C3的并，即X=Cay(G1，S)=C1∪C2∪C3(C1，C2，C3边互不相交)．

(2)在Wa,0和Wb,0间采用“标准型”分解方案中的(4)；

(3)在Wa,i中对H2β-2,o,i，H2β-3,1,i，…，Hβ+1,0,i，Hβ,1,i(i=1,3,5,…，α-1)进行H方操作；在Wa,j中对H2β-2,1,j，H2β-3,0,j，…，Hβ+1,0,j，Hβ,1,j(j=2,4,…，α-2)进行H方操作；

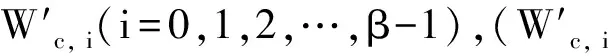
2) 设X=Cay(G，S)(S={a±1，b±1，c±1})为群G=〈a，b，c|a2β=1，aβ=bβ，aβ=cα，ab=ba，ac=ca，bc=cb〉(α、β均为奇数，β<α)的Cayley图．在X=Cay(G，S)中作如下操作，可将X=Cay(G，S)分解为3个边互不相交的Hamilton圈的并(见图2)：

(1)同1(1)；

(2)对Hβ-1,0,0，Hβ,1,0，Hβ+1,2,0，…，H2β-3,β-2,0进行H方操作；

(3)对H2β-3,0,t，H2β-4,1,t，H2β-5,0,t，H2β-6,1,t，…，Hβ,0,t，Hβ-1,1,t，(t=1，3，5，…，β-2)；

H2β-3,1,t，H2β-4,0,t，H2β-5,1,t，H2β-6,0,t，…，Hβ,1,t，Hβ-1,0,t，(t=2，4，6，…，β-3)；

H2β-2,1,t，H2β-3,0,t，…，Hβ+1,1,t，Hβ,0,t，(t=β-1，β+1，…，α-1)；

H2β-2,0,t，H2β-3,1,t，…，Hβ+1,0,t，Hβ,1,t，(t=β，β+2，…，α-2)进行H方操作；

证对(1)和(2)进行H方操作后，使得Ca形成X=Cay(G，S)的一个Hamilton圈O1，且使得Wc,i(i=0，1，2，…，α-1)各形成一个4度Cayley图的Hamilton圈．同时Wb,0，Wb,1也各形成一个4度Cayley图的Hamilton圈．

对(3)进行H方操作后，仍使得O1形成一个新Hamilton圈C1，且使得Wb,i(i=1，2，…，α-1)各形成一个4度Cayley图的Hamilton圈．

对(4)中(i)进行H方操作后，使得Cc形成X=Cay(G，S)的一个Hamilton圈O2，且使得Wb,0，Wb,1，Wb,2，…，Wb,β-1形成一个大的闭圈Ob(Ob通过Wb,0，Wb,1，Wb,2，…，Wb,β-1顶点恰好一次)．在Cc上利用“单向通道离合法”，即对(ii)进行H方操作后，使得O2仍形成一个新的Hamilton圈C3，且使得Cb形成X=Cay(G，S)的一个Hamilton圈C2，即X=Cay(G，S)=C1∪C2∪C3(C1，C2，C3边互不相交)．

3) 设X=Cay(G，S)(S={a±1，b±1，c±1})是群G=〈a，b，c|a10=1，a5=b5，a5=c6〉的Cayley图，在X=Cay(G，S)中进行如下操作可将其分解为3个边互不相交的Hamilton圈的并：

(2)在Wa,0中对H1,0,0，H2,1,0，H3,2,0，H1,3,0进行H方操作；

(3)对(i)H8,0,t，H7,1,t，H6,0,t，H5,1,t，(t=1，3，5)进行H方操作；(ii)H5,0,t，H6,1,t，H7,0,t，H8,1,t，(t=2，4)进行H方操作；

(4)对(b3c，b3c2，b4c2，b4c，b3c),(b2c2，b2c3，b3c3，b3c2，b2c2)，(bc3，bc4，b2c4，b2c3，bc3)，(c4，c5，bc5，bc4，c4)进行H方操作；

(5)在Wa,0中对(b3，b3c，b4c，b4，b3)进行H方操作．

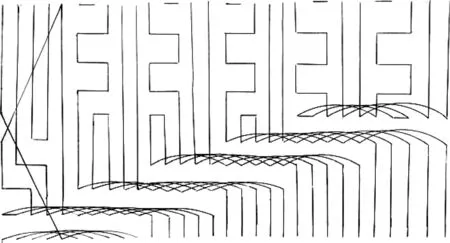
图3 Hamilton圈分解

图3为经过(1)、(2)和(3)操作后，得到X=Cay(G，S)的一个Hamilton圈O1，图3的中点bicj与a9bicj均由着色为a的边连接，i=1,2,3,4;j=0,1,2,3,4,5．

特别地，这里Wa,0中H方(b3，b3c，b4c，b4，b3)对O1具有Q特性[7]．只要证明在O1中有路径以点b4和b3c为端点即可[7]．

显然L=(b4，a5，a9，1，c，a9c，a9bc，bc，b，a9b，…，ab3，ab3c，ab3c2，b3c2，a9b3c2，a3b3c2，a3b3c3，…，a2b3c，a9b3c，b3c)为以b4和b3c为端点的路径．

一般地，设X=Cay(G，S)(S={a±1，b±1，c±1})为群G=〈a，b，c|a2β=1，aβ=bβ，aβ=cα〉(α为偶数，β为奇数，β<α)的Cayley图，在X=Cay(G，S)中进行如下操作,可将X=Cay(G，S)分解为3个边互不相交的Hamilton圈的并．

(1)同1)(1)；

(2)在Wa,0中对H1,0,0，H2,1,0，H3,2,0，…，Hβ-2,β-3,0，H2β-1,β-1,0，进行H方操作；

(3)同1)(3)；

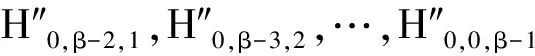
(5)对(bβ-2，bβ-2c，bβ-1c，bβ-1，bβ-2)进行H方操作．

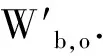
3 结论

当β为奇数，β<α时，群G=〈a，b，c|a2β=1，aβ=bα，aβ=cα，ab=ba，ac=ca，bc=cb〉的Cayley图X=Cay(G，S)(S={a±1，b±1，c±1})(记为Γ(β、α、α))与群G=〈a，b，c|a2β=1，aβ=bβ，aβ=cα，ab=ba，ac=ca，bc=cb〉的Cayley图X=Cay(G，S)(S={a±1，b±1，c±1})(记为Γ(β、β、α))均可分解为3个边互不相交的Hamilton圈的并．

参考文献：

[1] AKERS S B,KRISHNAMURTHY B.A group theoretic model for symmetric interconnection networks[J],IEEE Trans.Comput,1986(38)：216-223．

[2] AKERS S B,KRISHNAMURTHG B.The fault tolerance of star graphs,2nd Int Conf Supercomput[C].San Francisco,1987.

[3] ALSPACH B.Unsolved problem 4,5[J].Ann Discrete Math,1985(27):464-468.

[4] BERMOND J C,FAVARON O F,MAHEO M.Hamiltonian decomposition of Cayley graphs of degree 4[J].J Comb Theory,Ser B,1989(46):142-153.

[5] 王殿军，王建中.关于Abel群上Cayley图的Hamilton圈分解[J].数学进展，1994，23(4)：551-554.

[6] LIU J Q.Hamitonian decompositions of Cayley graphs on Abelian groups of odd order[J].J Comb Theory,Ser B,1996,66(1):75-86.

[7] 王艳芳.4度Cayley图的Hamilton圈分解的新方法与理论证明[J].纯粹数学与应用数学，2010，26(3):380-386.