姜 健

（江苏盐城技师学院，江苏 盐城 224002）

如何寻求辅助问题以实现“化归”

姜 健

（江苏盐城技师学院，江苏 盐城 224002）

在用“化归方法”解题的过程中，构造辅助问题是至关重要的，因为没有辅助问题，就不能将所给问题化为已经解决的问题，所以这是实现“化归”并最终解决问题的关键。

化归方法；辅助问题；揭露差异；逆向转化；突破创新

1 ．化而不归

众所周知，“化归方法”是一种间接方法，当所给问题直接下手较为困难时，即可构造辅助问题将其化为已经解决或较易解决的问题去处理。这就是所谓的“化归”策略。在“化归”的过程中，构造辅助问题乃是实施“化归”策略的关键，如果构造不了相应的辅助问题，那就不可能实现“化归”。由于辅助问题并非明显存在，且一般不易发现，故对大多数人来说，实施“化归方法”并非易事，往往会遭遇“化而不归”的尴尬。

例1 对于任意 x,y,z ∈ R ，试证：

直接从条件出发证明结论，几乎是不可能的，为此，必须运用“化归”策略，将原有问题加以转化。这就需要构造出相应的辅助问题，并借助辅助问题实现“化归”。但是，我们却不知其相应的辅助问题是什么，更不知从何下手去构造该辅助问题，所以只能是想“化”而“化不了”，即“化而不归”。

由此可知，“化归方法”虽好，但如不能解决如何有效地寻求辅助问题的话，那么这种方法就只能是徒有虚名而没有什么实际作用。正因为如此，所以寻求构造辅助问题的有效途径，从根本上解决“化而不归”的问题就成了我们的迫切任务。

2 ．突破创新

数学问题中存在着各种差异，这种差异就是条件与条件、条件与结论之间的不同点。而数学解题的过程，就是消除条件与条件、条件与结论之间的各种差异，并将条件转化为结论的过程。由于差异就是矛盾，所以这个过程就是一种矛盾转化的过程。而矛盾转化是有其客观规律的，即矛盾双方在一定条件下各自向其对立面转化，直到与对立面化同。《数学解题通论》中，正是以此转化规律为指导，提出了“揭露差异——逆向转化”的解题策略，从而有效地解决了寻求辅助问题的难题。

所谓“揭露差异”，就是将所给问题中条件与条件、条件与结论间的差异揭露出来。如“已知”与“未知”的差异、“一般”与“特殊”的差异、“整体”与“局部”的差异、“有限”与“无限”的差异、“运动”与“静止”的差异、“数”与“形”的差异、“多”与“少”的差异、“曲”与“直”的差异、“高”与“低”的差异等。

所谓“逆向转化”，就是让上述差异的双方各自向其对立面转化，如化“已知”为“未知”，化“未知”为“已知”；或化“一般”为“特殊”，化“特殊”为“一般”；以及化“动”为“静”，化“静”为“动”；或化“数”为“形”，化“形”为“数”等等。借助这些“逆向转化”，即可顺其自然地找到相应的辅助问题。下面我们运用这个方法来寻求辅助问题并借其解题。请看对例1的证明：

首先“揭露差异”：观察原问题，发现结论为不等式，其对立面为等式（或方程），所以本题存在着“等”与“不等”的差异。因此，证明本题可以采取如下的矛盾转化：“化不等为相等”及“化相等为不等”。

首先“化不等为相等”，即设法将不等式（1）转化为等式。由于x,y,z为未知数，因此这种等式即为方程。由于不等式（1）形似一元二次方程根的判别式，故可联想到构造一元二次方程。

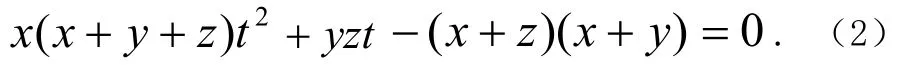
由此便实现了“化不等为相等”。

这就是所需构造的辅助问题，下面我们将借其完成证明。为此，尚需“逆向转化”，即“化相等为不等”。

∵方程（2）的系数和为

∴方程（2）有实根1.

又∵ x,y,z∈ R，∴方程（2）的系数为实数，

∴方程（2）的判别式为非负，即

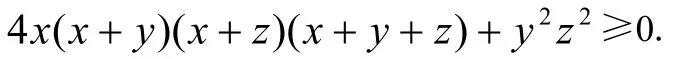
于是又“化相等为不等”。

若x(x +y +z)=0，则不等式（1）显然成立。

从而原不等式得证。

这样，借助于“等”与“不等”的转换，我们就在不知不觉中找到了辅助问题——方程（2），它是条件与结论间的内在联系，通过它的桥梁作用即可顺利导致证明。

从以上的证明过程中不难看出，我们是在矛盾分析与矛盾转化的基础上完成证明的，是按照矛盾转化的规律办事的。证明过程循序渐进、和谐自然，没有人为雕琢的痕迹。以例1为例，我们没有执意将结论式的左端配成平方，而是在矛盾分析后，先化不等式为等式，并由此得到启发，构造出相应的辅助方程（2），然后再“逆向转化”，化等式为不等式，即将方程（2）转化为不等式，为此只需利用一元二次方程有实根的条件，即可证明不等式（1）。

尽管在构造辅助方程（2）时少不了用到个人的一些直觉与经验，但因是根据客观规律办事，所以能够有所遵循，并不需要盲目探索。事实上，在“化不等为相等”的启发下，自然会想到构造一个等式，这里即是方程；而根据不等式的特点，也只能想到构造相应的一元二次方程。不过这个方程究竟如何构造，则是需要有一点聪明才智的，其中的关键就是方程（2）根的判别式应与结论式一致，且各项系数的和必须为零，这样才能使其有实根1，才能确保判别式非负，从而导致结论的证明。所以此法虽然不依赖于个人的聪明才智，但也不完全排除个人才智的作用。

3 ．原理浅析

在解决数学问题的过程中，寻求条件与结论间的内在联系是至关重要的，因为它是实现条件向结论转化的桥梁，也是构造辅助问题的基础。而“揭露差异——逆向转化”则有助于揭示这种联系。

在数学问题中，差异乃是表象，而内在联系则是本质。由于本质常被表象所掩盖，因此如果用形而上学的观点去看问题，就很难发现这种本质联系，这就是我们难以找到辅助问题的原因。

但如采取“揭露差异——逆向转化”的做法，那就不是用形而上学而是用唯物辩证的观点去处看待数学问题了。由于“揭露差异——逆向转化”破坏了原有的数学问题的关系结构，使得差异与联系发生转化，从而消除了表象对本质的掩盖，将内在联系充分地暴露出来。这就是为什么能够较易找到辅助问题并较易解决问题的原因。

不难看出，遵循这种做法，就能使我们有章可循、有法可依，从而克服盲目性，提高自觉性，提高解题效率。这是一种全新的数学解题模式。它不仅适用于才智较高的学生，而且也适用于才智一般的学生，因此不仅适用于精英教育，而且更适用于大众教育。在提倡素质教育与大众教育的今天，我们就应在数学教学中大力推广这种方法，以便全面提高学生的数学素养与解决问题能力。

[1] 顾越岭. 数学解题通论[M]. 广西教育出版社，2000.

G42

A

1008-7427（2011）06-0126-01

2011-03-23

作者系江苏盐城技师学院高级讲师。