● (湖南师范大学数学奥林匹克研究所 湖南长沙 410081)

我们称对边乘积相等的圆内接四边形为调和四边形，调和四边形有如下有趣的性质.

性质1圆内接四边形为调和四边形的充要条件是对角平分线的交点在另一对顶点的对角线上.

证明如图1，设ABCD是圆内接四边形.

充分性设∠B平分线与∠D平分线的交点T在对角线AC上，则由角平分线的性质知

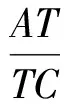
从而

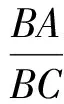
即

AB·CD=BC·DA.

必要性由AB·CD=BC·DA,得

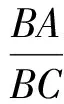
设∠B的平分线交AC于点T1,∠D的平分线交AC于点T2，则

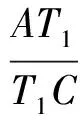
从而

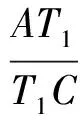
即

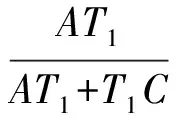
因此AT1=AT2,即点T1与T2重合，故∠B角平分线与∠D角平分线的交点在对角线AC上.

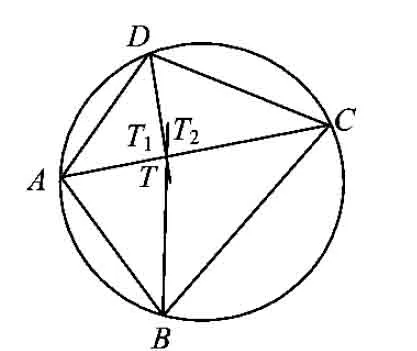
图1

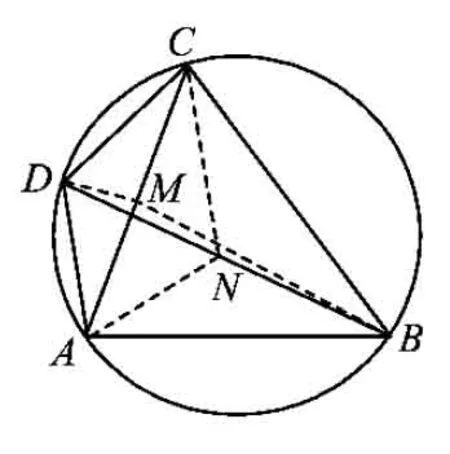
图2

性质2圆内接四边形为调和四边形的充要条件是2条对角线的中点是四边形的等角共轭点.

证明如图2，设M，N分别是圆内接四边形ABCD的对角线AC，BD的中点.

充分性若M，N是四边形ABCD的等角共轭点，即

(1)

(2)

由式(1)，并注意到

∠DCM=∠DCA=∠DBA,

得

△DCM∽△DBA,

即

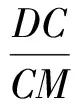
因此

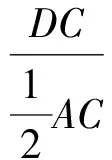
故

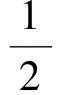
(3)

由式(2)得∠DAN=∠CAB,再注意到∠ADN=∠ADB=∠ACB,则△ABC～△AND,得

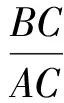
于是

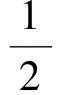
(4)

由式(3)，式(4)得

AB·CD=BC·DA.

必要性若AB·CD=BC·DA,由托勒密定理AB·CD+BC·DA=AC·BD,得

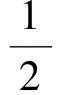
即

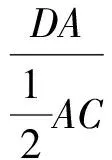
又由∠DAM=∠DAC=∠DBC,得

从而

∠ADM=∠BDC=∠NDC,

同理可得∠DCM=∠BCN,∠CBN=∠ABM,∠BAN=∠DAM,故M，N为四边形ABCD的等角共轭点.

性质3圆内接四边形为调和四边形的充要条件是以每边为弦且与相邻的一边相切于弦的端点的圆交过切点的一条对角线于中点.

证明如图3，设M，N分别是圆内接四边形ABCD的对角线AC，BD的中点.

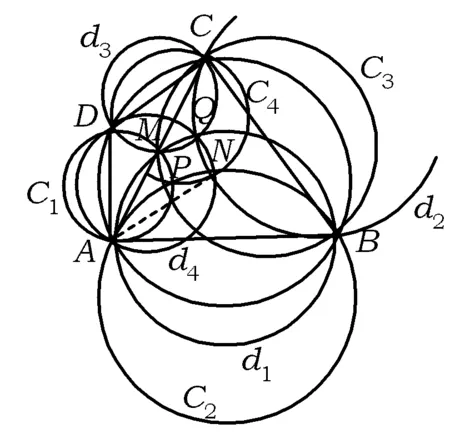
图3

充要性记过点D与AB切于点A的圆为C1,过点A与BC切于点B的圆为C2，依次得C3,C4；记过点B与DA切于点A的圆为d1,过点C与AB切于点B的圆为d2，依次得d3,d4.

当C1过点M时，由弦切角定理知

∠ADM=∠MAB=∠CAB=∠CDB=∠CDN,

即

∠ADM=∠CDN.

当C2过点N时，由弦切角定理知

∠BAN=∠NBC=∠DBC=∠DAC=∠DAM,

即

∠BAN=∠DAM,

同理可得 ∠ABM=∠CBN,∠BCN=∠DCM，

从而点M，N为四边形ABCD的等角共轭点.又M，N分别为AC，BD的中点，由性质2知ABCD为调和四边形.

必要性由性质2证明中的式(5)得

△DAM∽△DBC，

从而

∠ADM=∠BDC=∠CAB=∠MAB.

由弦切角定理的逆定理，知点M在圆C1上.同理可得，M在圆d1,C3,d3上；N在圆C2,d2,C4,d4上.

推论1在调和四边形ABCD中，性质3中的圆C1,d1,C3,d3共点于AC的中点M，圆C2,d2,C4,d4共点于BD的中点N.

推论2在调和四边形ABCD中，性质3中的圆C1,C2,C3,C4共点，圆d1,d2,d3,d4共点.

事实上，若设圆C1与C2交于点P，则

∠MPB=∠MDA+∠PAB+∠PBA=

∠CDB+∠PAB+∠PBA=

∠CAB+∠PBC+∠PBA=

∠CAB+∠ABC=180°-∠MCB,

从而M，P，B，C四点共圆，即圆C3过点P.同理，C4也过点P，故C1,C2,C3,C4共点于P.同理可得，d1,d2,d3,d4共点于Q.

注还可证得P，Q也是四边形ABCD的等角共轭点.

性质4圆内接四边形为调和四边形的充要条件是对顶点处的2条切线与另一对顶点的对角线所在直线三线共点或互相平行.

证明当四边形为菱形时，对顶点处的2条切线与另一对顶点的对角线所在直线互相平行.

下面讨论四边形不为菱形的情形.

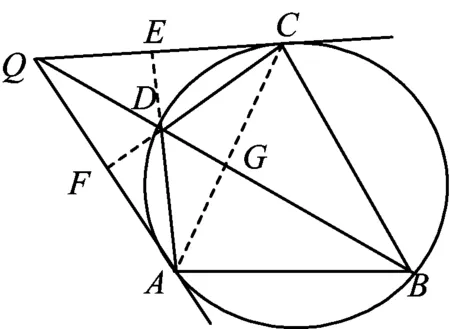
图4

如图4，点Q是圆内接四边形ABCD的分别过顶点A，C的切线的交点.

充分性当点Q在直线DB上时，则由QA=QC,△QAD∽△QBA,△QCD∽△QBC,得

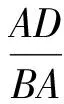
故

AB·CD=BC·DA.

必要性当AB·CD=BC·DA时，由正弦定理得

sin∠ADB·sin∠DBC=sin∠BDC·sin∠DBA.

连结AC交BD于点G，延长AD交QC于点E，延长CD交QA于点F，则

∠CAF=∠ECA.

从而

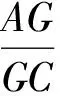
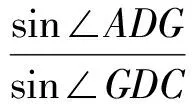
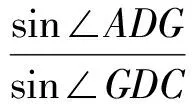
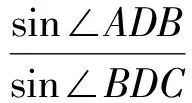
对△ACD应用塞瓦定理的逆定理，知AF，GD，CE共点于Q.故过A，C的2条切线与直线DB共点于Q.

注此性质提供了作调和四边形的一种方法：先作出一个圆内接三角形，在一顶点处作圆的切线，再将此顶点所对边延长.若这2条线相交，则由交点作圆的另一条切线，所得切点与原三角形3个顶点组成调和四边形的4个顶点；若这2条线平行，则作与前面切线平行的圆的另一切线，所得切点与原三角形3个顶点组成调和四边形的4个顶点.

性质5圆内接四边形ABCD为调和四边形的充要条件是过点C作CT∥DB交圆于T，点T与DM的中点M，A三点共线.

证明如图5，由CT∥DB知,DBTC为等腰梯形，连结BT，DT，则

DC=BT,DT=BC.

注意到∠ABT与∠TDA互补，则

AB·CD=BC·DA,

即

AB·BT=DT·DA,

从而

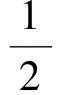
即

S△ABT=S△ADT,

从而直线AT过DB的中点M,故T,M,A三点共线.

注此性质也提供了作调和四边形的一种方法：先作出一个圆内接三角形，在一顶点处作与所对边的平行线交圆于一点，此点与这条边的中点的连线交圆于另一点，这另一点和三角形3个顶点组成调和四边形的4个顶点.

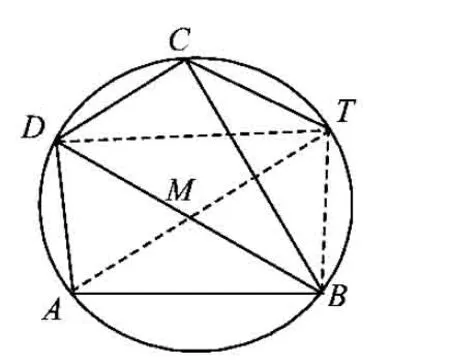
图5

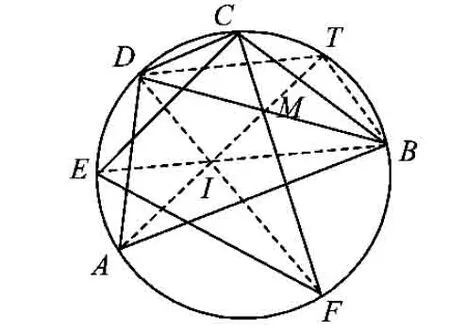
图6

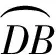
证明如图6，由题设知D，I，F三点共线，B，I，E三点共线.由I为△CEF的内心，注意CT∥DB,有ID=DC=BT,IB=BC=DT.从而IBTD为平行四边形，即TI过DB的中点M.故由性质5知

AB·CD=BC·DA,

即T，M，A三点共线,TI过BD的中点M.

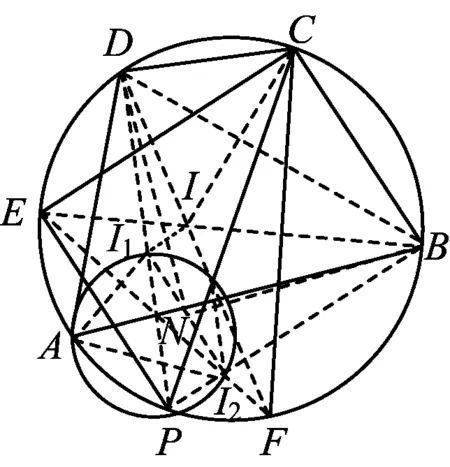
图7

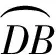
证明如图7，由题设知P，I1，D及P，I2,B分别三点共线.连结I1A,I2A,则

∠I1DA=∠I2BA,∠I1PI2=∠BPD=∠BAD.

又由内心的性质,得

CD=I1D,BC=I2B,

于是

AB·CD=BC·DA,

即

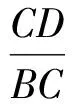
从而

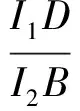
得

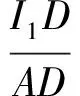
于是

△I1DA∽△I2BA,

得

∠I1AD=∠I2AB,

即

∠I1AI2=∠I1PI2,

于是A,P,I2,I1四点共圆.

推论1设△CEF的内心为I,则I1I⊥I2I.

证明 如图7,注意内心所张的角与对应顶角的关系,知

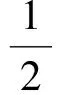
即E,I1,I,C四点共圆,则

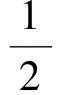
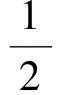
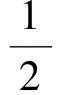
同理可得

∠EII1=∠IFI2,

从而

△EI1I∽△II2F.

于是

∠EII1+∠FII2=∠EII1+∠I1EI=

180°-∠EI1I=∠ECI=

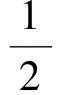
所以

∠I1II2=∠EIF-(∠EII1+∠FII2)=

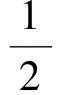
故

I1I⊥I2I.

推论2设N为I1I2的中点，则BN⊥DN.

证明如图7，由D，I，F共线及内心的性质得

DI=DC,DI1=DC，

从而

DI=DI1.

由推论1知I1I⊥I2I，有IN=I1N.注意到DN为公共线，则△DNI1≌△DNI,从而

同理可得

又

所以

∠NDB+∠NBD=

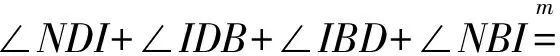
即

∠BND=90°,

故

BN⊥DN.

下面给出上述性质应用的一些例子.

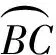
(1)△PI1I2的外接圆过定点；

(2)以I1I2为直径的圆过定点；

(3)I1I2的中点在定圆上.

(2003年国家集训队培训题)

事实上，可参见图7，利用性质7及推论1，推论2即可证得结论成立.对于第(1)小题，视例1中的△ABC为图7中的△CEF，则△PI1I2的外接圆过定点为图7中的点A；对于第(2)小题，由推论1有I1I⊥I2T,知以I1I2为直径的圆过定点I；对于第(3)小题，由推论2知，I1I2的中点在以图7中的以DB为直径的定圆上.

(2008年国家集训队测试题)

事实上，可参见图7，图6，利用性质7，性质6即可证得结论.

例3已知直线上的3个定点依次为A，B，C，Γ为过A，C且圆心不在AC上的圆，分别过点A，C且与圆Γ相切的直线交于点P，PB与圆Γ交于点Q，证明：∠AQC的平分线与AC的交点不依赖于圆Γ的选取.

(第45届IMO预选题)

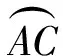
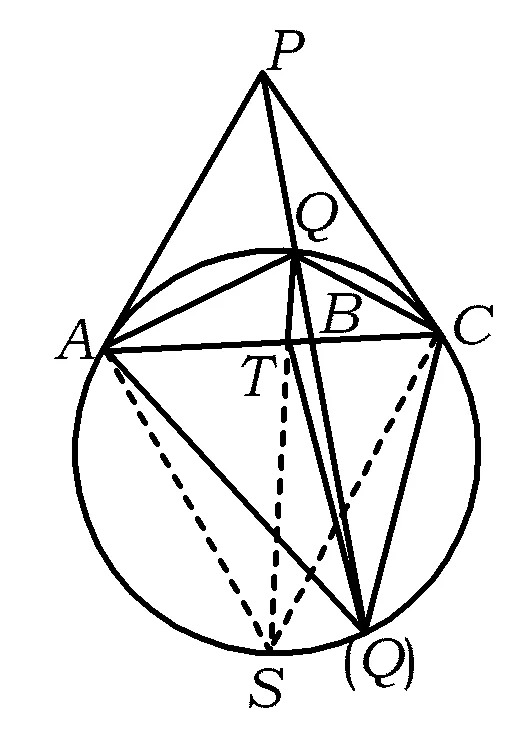
图8

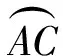
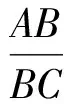
同理在等腰△ASC中，有

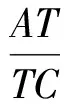
在△PAC中，视Q为塞瓦点，由角元形式的塞瓦定理得

注意到∠PAQ=∠ASQ=∠QCA,∠PCQ=∠CSQ=∠QAC,则

即

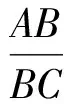
亦即

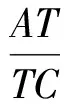
故T不依赖于圆Γ的选取.

例4设△ABC的内切圆分别切BC，CA，AB于点D，E，F，点M是圆上任一点，且MB，MC分别交圆于点Y，Z.证明：EY，FZ，MD三线共点.

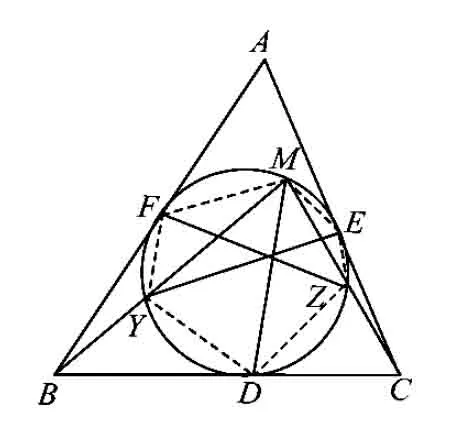
图9

图10

证明如图9，连结有关点得圆内接六边形FYDZEM.根据塞瓦定理的推论(即对塞瓦定理的角元形式应用正弦定理推得)，有EY，FZ，MD三线共点,从而

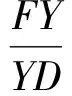
由性质4，在四边形FYDM中，得

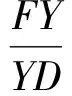
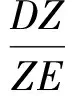
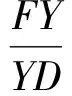
故结论获证.

例5设△ABC的内切圆分别切BC，CA，AB于点D，E，F，AD与圆交于点M，AB，MC分别交圆于点Y，Z.证明：FY∥MD∥EZ的充要条件是点M为AD的中点.

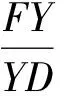
反之，由FY∥AD，得

∠FAM=∠BFY=∠FDY.

又由∠FMA=∠FYD,得

△FMA∽△FYD,

即

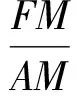
注意到性质4，有

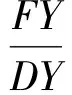
故AM=MD.必要性得证.

例6∠APB内有一内切圆与边切于点A，B，PCD是任一割线交圆于点C，D，点Q在CD上，且∠QAD=∠PBC.证明：∠PAC=∠QBD.

(2003年全国高中数学联赛加试题)

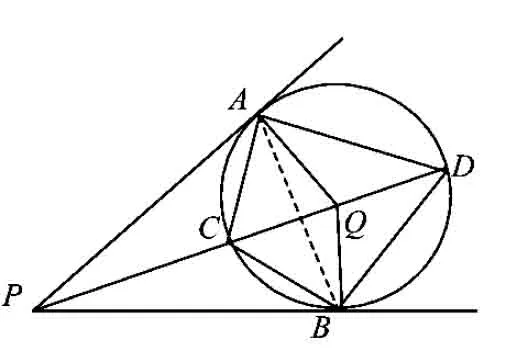
图11

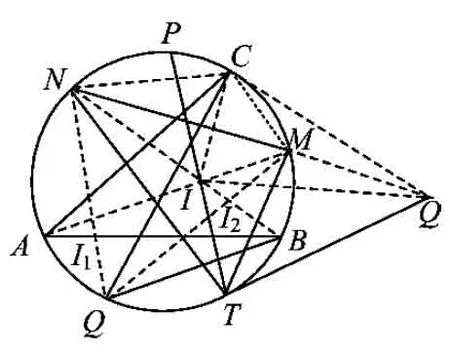
图12

证明如图11，由弦切角定理得

∠PAC=∠ADQ,∠PBC=∠QDB,

从而由∠QAD=∠PBC,得

连结AB，则

∠CBA=∠CDA=∠QDA,

∠CAB=∠PBC=∠QAD,

即知△ACB∽△AQD,从而

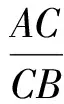
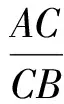
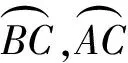
(1)求证：MP·MT=NP·NT;

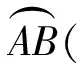
(2009年全国高中联赛加试题)

(1)证法1因P，I，T共线，由性质6，即知TMCN为调和四边形，即

MT·NC=NT·MC.

又由PC∥NM知NMCP为等腰梯形，得

NC=MP,MC=NP,

故

MP·MT=NP·NT.

证法2分别过点C，T作圆的切线相交于点Q.下证点Q在直线NM上，如图12.

事实上，可知A，I，M共线，B，I，N共线，由内心性质知

MC=MI,NC=NI,

从而MN⊥CI.又PC∥NM，得PC⊥CI,即∠PCI=90°，于是

∠CIP=90°-∠CPI=90°-∠CPT=

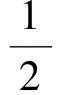
从而点Q为△CTI的外心，即QI=QC,从而Q在CI的中垂线MN上，故点Q，M，N共线.

注意到性质4，即知TMCN为调和四边形，下同证法1.

(2)由性质7即可证得.

[1] 尚强.初等数学复习及研究(平面几何)习题解答[M].哈尔滨：哈尔滨工业大学出版社，2009.

[2] 沈文选.走向国际数学奥林匹克的平面几何试题诠释[M].哈尔滨：哈尔滨工业大学出版社，2007.