王宇飞 吴庆宪 姜长生

(南京航空航天大学自动化学院，南京 210016)

作为一种性能良好的逼近器［1－2］，模糊系统被广泛应用于非线性系统的建模中［3－5］.模糊方法备受研究者关注，尤其是T－S模糊方法.传统的模糊逼近对象是根据专家经验建立的，虽然其基本上可以反映系统的非线性动态特性，但模糊子系统参数一旦确定后将不再变更.而实际中，当模型本身的参数一旦发生调整，已建立的模糊逼近对象将无法适应此类变化，大大影响控制效果.引入优化训练算法可在线调整模糊逼近器，提高逼近精度，适应系统模型参数的变化.

Levenberg－Marquardt(L－M)算法［6］是一种著名的寻优算法，尤其在神经网络的批处理训练中通常被认为是最好的算法之一，其训练精度和训练速率都优于BP、共轭梯度法、高斯－牛顿法等算法［7－9］.但是当L－M算法用于求解线性方程组时，要求方程组解处的Jacobi矩阵非奇异，这一条件往往过强，可以通过引入局部误差界的定义来弱化此条件［10－12］.基于模糊系统的万能逼近特性［13］，L－M 算法还可用于T－S模糊系统训练［14］，使其不过分依赖于专家经验，有效逼近复杂非线性系统及函数，且可对各线性多项式的参数及模糊隶属度函数的参数进行在线调节，大大提高了训练时的收敛速率.

基于以上分析，本文在局部误差界条件下，研究了一种新的L－M参数迭代算法，并将其推广应用于T－S模糊系统的建模中.该算法可在线训练各线性多项式的参数及模糊隶属度函数的参数，有效避免Jacobi矩阵奇异并加快收敛速率.最后，将该算法应用于NSV系统的模糊建模训练中.仿真结果表明，与标准L－M算法相比，该算法的收敛速率明显加快.

1 NSV姿态系统建模

1.1 NSV姿态系统

假设NSV是一个刚体，那么其姿态系统可以表示为

式中，x(t)={ωT，ΩT}T∈R6;Ω ={α，β，μ}T∈R3为姿态角;α，β，μ 分别为攻角、侧滑角和滚转角;ω ={p，q，r}T∈R3为角速率;u(t)∈R3为控制力矩;g(x)∈R6×R3为输入矩阵;Δ(x)∈R6为不确定部分;f(x)∈R6为非线性的，可表示为

可以看出，NSV姿态系统是高度非线性和强耦合的，并且含有不确定部分，这使控制器的设计增加了难度.采用模糊系统可以逼近系统的特性.传统的模糊系统需要依靠专家经验，这在实现过程中是比较困难的，但利用L－M算法就可以解决这个问题.

1.2 训练方案

基于L－M算法的T－S模糊在线逼近方案如图1所示.采用输入输出的采样数据(xk，yk)(k为迭代次数，且k=1，2，…)的信息，基于T－S模糊理论来构建模糊逼近器FTS，逼近器参数θ0可在线调节.

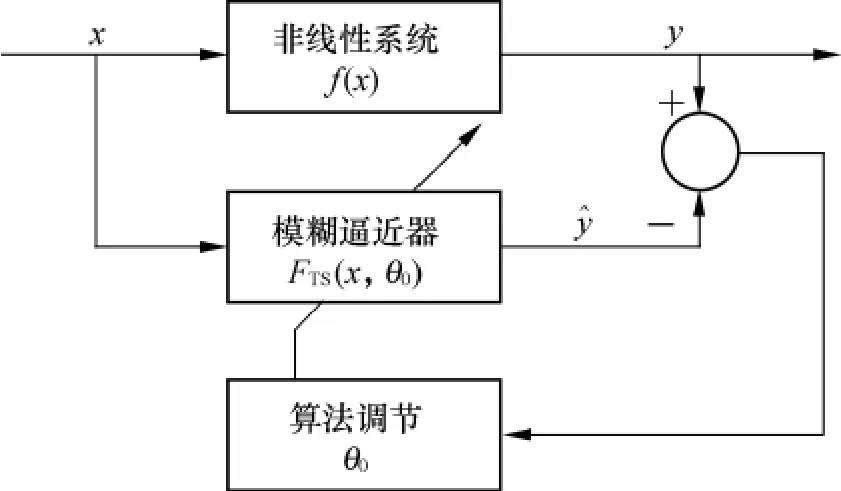
图1 L－M算法模糊在线逼近方案

基于T－S模糊系统的逼近器可表示为

式中，^y=FTS(x，θ0)为模糊逼近输出;pi(x)=ai，0+ai，1x1+ …+ai，nxn(i=1，2，…，R;j=0，1，2，…，n)为后件函数;为组成T－S模糊系统的第i个模糊规则的模糊权函数;分别为第i个模糊规则下xj的隶属度函数的中心和宽度.

模糊规则定义如下:

若有如下定义:

则T－S模糊系统可表示为

若要求隶属度函数的中心和宽度均可在线调节，则定义参数θ∈Rp为

2 改进L-M算法及模糊系统训练

2.1 标准L-M算法

在标准L－M算法中，逼近误差可定义为

式中，ε(θ):Rp→RM(i=1，2，…，M)为连续可微函数;M为逼近对象y的数据采样点的个数.在本文中，假设当迭代次数k→∞时，ε(θ)=0解集非空，记为Θ*.

性能指标函数定义为

迭代求解参数θ的修正公式为

式中，k为迭代次数;Γ(θk)=ε′(θk)为 Jacobi矩阵;Λk= λkI∈Rp×p为对角正定阵，以保证 Γ(θk)TΓ(θk)+Λk正定且可逆.

2.2 改进L-M算法

在标准L－M算法中，将λk取为常数.本文考虑的是在局部误差界下一种基于信赖域的全局收敛的LM算法，根据逼近效果可实时调节步长，以进一步改善L－M算法的收敛速率.因此，先给出局部误差界的定义.

定义1 设 N⊂Rp，且满足 N∩Θ*≠∅.如果存在常数 c＞0，使得‖ε(θ)‖≥cdist(θ，Θ*)，∀θ∈N，则称ε(θ)在N内有局部误差界.其中 dist(θ，Θ*)=minϑ∈Θ*‖θ－ϑ‖，局部误差界条件比非奇异性条件弱.

选取迭代参数λk=αk‖εk‖，指标函数由式(9)式给出，则第k步迭代的实际下降量和预测下降量分别为

实际下降量与预测下降量的比值为

下面，给出改进L－M算法的步骤如下:

① 给定 θ1∈Rp，ξ≥0，0 ＜m ＜ α1，0≤β0≤β1≤β2＜1，k:=1.

② 若‖(Γk)Tεk‖≤ξ，则终止算法;否则，取 λk=αk‖εk‖，求解得到 Δθk.

③ 计算 rk=Ak/Pk，令

④计算

⑤令k:=k+1，转至步骤②.

2.3 基于改进L-M算法的T-S模糊系统训练

训练的目标是当迭代数k→∞时y→^y.当采用改进的L－M 算法训练T－S模糊系统时，逼近误差可表示为

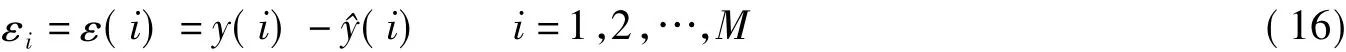
误差向量ε是参数θ的函数;权值增量Δθ可由2.2节中改进L－M算法得到.用于模糊系统训练时，Jacobi矩阵Γ(θ)定义如下:

同理可得FTS(x(i*)，θ)对参数θ其余分量的偏导数.鉴于篇幅，下面仅给出FTS(·)对，aj*，0，aj*，1的偏导表达式，即

至此，得到了Jacobi矩阵Γ(θ)中各元素的表达式，改进的L－M 算法就可以对T－S模糊系统进行训练了.

3 在NSV姿态系统模糊建模中的应用

为验证本文算法的有效性，并与标准L－M算法进行比较，下面对NSV姿态系统中非线性函数f2(x)进行模糊逼近.

3.1 参数的选择与初始化

一般来说，p，q，r∈［－0.5，0.5］，α，β，μ∈［－0.5，0.5］，故限制各隶属度函数的中心均在此范围内，而隶属度函数的宽度限制在［0.01，1］之间.

各隶属度函数中心的初始值在［－0.5，0.5］均匀分布，宽度的初始值分别为0.5.θ0的初始值选为0.

取 ξ=0.01，m=1 ×10－8，β0=1 ×10－4，β1=0.25，β2=0.75，α1=0.5.

3.2 仿真结果

x1是f2(x)中的关键变量，故而仅给出函数分量f2(x)关于变量x1的模糊逼近及逼近误差仿真效果图(见图2和图3).

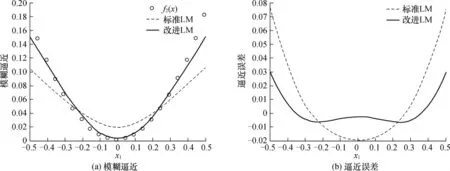
图2 1次迭代逼近f2(x)的结果

图3 2次迭代逼近f2(x)的结果

当逼近误差小于0.01时，L－M算法停止迭代.由图3可知，本文算法在迭代2次后就已达到规定的误差精度，算法收敛速率优于标准L－M算法.

4 结语

本文提出了一种用于T－S模糊系统训练的改进的全局收敛L－M 算法.采用L－M 算法训练T－S模糊系统，可在线调节各线性系统的参数及模糊隶属度函数的参数，使系统建模时不用过分依赖于专家经验，从而大大提高了T－S模糊系统逼近复杂非线性系统的收敛速率.将本文算法应用于训练T－S模糊系统，以逼近NSV姿态系统.仿真结果表明，与标准L－M算法相比，本文算法在保证精度的同时，收敛速率明显加快.由此可知，本文算法可有效提高L－M算法训练T－S模糊系统的收敛速率.

References)

［1］ Wang L X.Fuzzy systems are universal approximators［C］//Proceeding of the 1992 IEEE International Conference on Fuzzy Systems.San Diego，CA，USA，1992:1163－1170.

［2］ Ying H.General Takagi－Sugeno fuzzy systems are universal approximators［C］//Proceedings of the 1998 IEEE Interna－tional Conference on Fuzzy Systems.Anchorage，AK，USA，1998:819－823.

［3］ Onut S，Saglam C O.Modeling and optimization of general cargo port operations through fuzzy minimal spanning tree and fuzzy dynamic programming approaches ［J］.International Journal of Innovative Computing，Information and Control，2008，4(8):1835－1851.

［4］ Takagi T，Sugeno M.Fuzzy identification of systems and its applications to modeling and control［J］.IEEE Transactions on Systems，Man and Cybernetics，1985，15(1):116－132.

［5］ Wang Y H，Wu Q X，Jiang C S，et al.Acceleration of Levenberg－Marquardt method training of chaotic systems fuzzy modeling ［J］.World Journal of Modeling and Simulation，2007，3(4):289－298.

［6］ Marquardt D.An algorithm for least squares estimation of nonlinear parameters［J］.Journal of the Society for Industry and Applied Mathematics，1963，11(2):431－441.

［7］ Hagan M T，Menhaj M B.Training feedforward networks with the Marquardt algorithm［J］.IEEE Transactions on Neural Networks，1994，5(6):989－993.

［8］ Chen T C，Han D J.Acceleration of Levenberg－Marquardt training of neural networks with variable decay rate［C］//Proceedings of the International Joint Conference on Neural Networks.New York，USA，2003:1873－1878.

［9］ Amir A S，Mohammad B T，Abbas H.Modified Levenberg－Marquardt method for neural networks training［J］.World Academy of Science，Engineering and Technology，2005，6(6):46－48.

［10］ Yamashita N，Fukushima M.On the rate of the convergence of the Levenberg－Marquardt method［J］.Computing，2001，15(Sup1):239－249.

［11］ Fan J Y，Yuan Y X.On the quadratic convergence of the Levenberg－Marquardt method without nonsingularity assumption［J］.Computing，2005，74(1):23－39.

［12］ Yang L，Chen Y P.A new globally convergent Levenberg－Marquardt method for solving nonlinear system of equations［J］.Mathematic Numerica Sinica，2008，30(4):388－396.

［13］ Wang L X.Universal approximation by hierarchical fuzzy systems［J］.Fuzzy Sets and Systems，1998，93(3):223－230.

［14］ Passino K M.Biomimicry for optimization，control and automation［M］.London，UK:Springer－Verlag，2005.