夏章生

(湖北民族学院 理学院，湖北 恩施 445000)

1985年，小子模(small submodules)作为本质子模(essential submodules)的对偶概念，被Tiwary和Chaubey引入到投射(projective)类模体系的研究之中.定义了小投射模(small projective module)[1]的概念，即下面的图1交换.本文将应用本质子模来证明内射模(injective modules)是与小投射模相对偶的概念，并用本质理想来刻画几类的环：Noether环、hereditary环、V-环和半单环等.本文中将用R记带有单位元1的结合环，所有模都是左酉R-模.先回顾本质子模的概念.

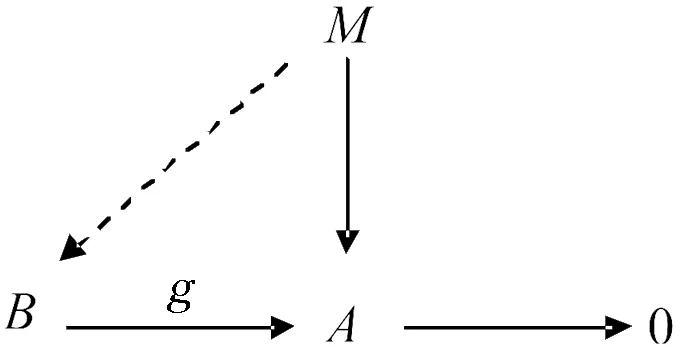
图1 小投射模

定义1 一个模M的子模N称为本质子模，如果对M的任意非零子模L，都有N∩L≠0.

定理1 对一个左R-模M来说，下列命题等价：

(i)M是内射模；

(ii)对一个模B的任意本质子模A，每个同态映射f∶A→M都可扩充成同态映射g∶B→M；

(iii)对R的每个本质理想I，每个同态映射f∶I→M都可扩充成同态映射g∶R→M.

证明(i)⟹(iii)由内射模的定义可知.

(iii)⟹(ii) 假定A是模B的一个任意本质子模，f∈HomR(A,M).考虑集合：

Ω={(C,g)|A⊆C⊆B,g∈Hom(C,M),g|A=f}，并在Ω中定义一个偏序关系≤如下：(C,g)≤(D,h)⟺C⊆D,h|C=g.

因为(A,f)∈Ω，故Ω非空.由Zorn引理，Ω存在一个极大元(C0,g0).若C0=B，则命题(iii)得证.假定C0≠B，取x0∈BC0，先证明集合I={r∈R|rx0∈C0}是R的一个本质理想.实际上，若L是R的一个非零左理想，0≠x0∈L，则有：I∩L≠0.因为，若r0x0=0，则r0∈I，0≠r0∈I∩L；否则，Rr0x0是B的一个非零左R-模，由A是B的本质子模和A⊆C0⊆B，得C0也是B的本质子模，从而C0∩Rr0x0≠0，取0≠rr0x0∈C0∩Rr0x0，r∈R，有0≠rr0∈I∩L.定义h:I→M;rg0(rx0),r∈R.由假设，存在同态映射h′∶R→M，使得定义C1=C0+Rx0，且:g1∶C1→M;c0+rx0g0(c0)+h′(r),c0∈C0,r∈R.

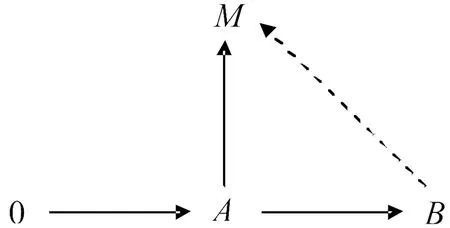
图2 内射模

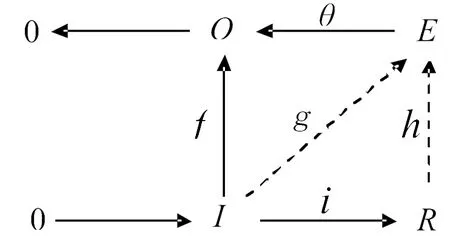
图3 带正合行的交换图

易证g1是定义良好的，且g0=g1|C0.从而(C1,g1)∈Ω，与(C0,g0)是Ω中极大元相矛盾.因此，C0=B.

(ii)⟹(i) 设E是M的内射包(injective envelope)，则M是E的本质子模，恒等映射1M∶M→M可扩充成同态映射g∶E→M.因而，M是E的直和项，得M也是内射模.证毕.

实质上，定理1的命题(ii)等价于：对一个模B的任意本质子模A，下面的图2交换.可以看出，小投射模是与内射模相对偶的一类模.我们知道，一个环R是左Noether环，如果每个左理想是有限生成的；R是左hereditary环，如果每个左理想是投射模；R是左V-环[3]，如果每个单左R-模是内射的.下面将用本质左理想来刻画这些环.

推论2 对一个环R，下列命题等价：

(i)环R是左Noether环；(ii)每个本质左理想是有限生成的；

(iii)若干个内射模的直和也是内射模.

证明(i)⟹(ii) 由定义显然.

(ii)⟹(iii) 设{Ei}i∈I是一族内射模，L是R的左本质理想，且f∈Hom(L,Ei).因为L是有限生成的，得f(L)也是有限生成的，从而存在I的有限子集{i1,i2,…,in}，使得f(L)⊆Ei1⊕Ei2⊕…⊕Ein.又Ei1,Ei2,…,Ein是内射模，得Ei1⊕…⊕Ein也是内射模，故存在同态映射g∈Hom(R,Ei1⊕Ei1⊕…⊕Ein)，亦即g∈Hom(R,Ei)，使得g|L=f.由定理1，得Ei是内射模.

(iii)⟹(i) 由文献[2]中定理4.10可得.证毕.

推论3 一个环R，下列命题等价：

(i)环R是左Hereditary环；(ii)每个本质左理想都是投射模；(iii)内射模的每个商模都是内射模.

证明(i)⟹(ii) 由定义显然.

(ii)⟹(iii) 考虑下面带有正合行的交换图3：

其中I是R的本质左理想，Q是一个内射模E的商模，f∈Hom(I,Q)，i和θ分别是自然的同态单射和同态满射.因为I是投射模，则f可以提升为同态映射g∶I→E，即f=θg.又E是内射模，g可以扩充为同态映射h∶R→E，即f=gi.从而，f=(θh)i，由定理1，得Q是内射模.

(iii)⟹(i) 由文献[2]中定理4.23可得.证毕.

推论4 对一个环R，下列命题等价：

(i)环R是左V-环；(ii)R的每个左理想I都是所有包含I的极大左理想的交；(iii)R的每个本质左理想的任意极大左子理想I都是所有包含I的极大左理想的交.

证明(i)⟹(ii) 由文献[3]中定理1可得.(ii)⟹(iii) 显然.(iii)⟹(i) 设S是一个单左R-模，L是R的一个本质左理想，且0≠f∈Hom(L,S).由S是单的，得K=Kerf是L的一个极大左子理想，从而K是所有包含K的极大左理想的交.故存在R的一个极大左理想M，使得K⊆M，但L⊄M.因而，有：R=L+M，且L∩M=K.定义：g∶R→M;l+mf(l),l∈L,m∈M,则g是定义良好的，且g扩充了f.因此，S是内射模，且R是左V-环.证毕

定理5 环R是半单的当且仅当每个本质左理想是内射模.

证明若R的本质左理想是内射模，则它也是R的一个直和项.同时，由于它是本质子模，它必定是R自身.因此：Soc(RR)=∩{I|I是R的本质左理想}=R，即RR是半单的，所以环R是半单环.证毕.

[1] Tiway A K,Chaubey K N.Small projective modules[J].J Pure Apll Math,1985,16(2):133-138.

[2] Rotman J J.An introduction to homological algebra[M].New York:Academic Press Inc,1979.

[3] Michler G O,Villamayor O E.On rings whose simple modules are injective[J].J Algebra,1973,25:185-201.