【摘  要】  对2023年陕西中考13题从试题结构、知识能力、思维障碍、解法探究、作业设计等角度进行深度分析，提出雕刻试题让思维进阶、技术赋能助思维成长、从核心概念出发构建知识体系，育高阶深度思维品质.

【关键词】  几何直观;数形结合;作业;数学见识

1  试题呈现  图1

（陕西省2023年中考数学第13题）如图1，在矩形ABCD中，AB=3，BC=4，点E在边AD上，且ED=3，M，N分别为边AB，BC上的动点，且BM=BN，P是线段CE上的动点，连接PM，PN，若PM+PN=4，则线段PC的长为.2  试题简析

试题属于填空压轴题，以矩形为载体，隐藏角平分线、等腰直角三角形，构造内涵丰富、思辨灵动的图形空间.试题综合考查学生灵活运用矩形性质定理、轴对称性质、平行线之间的距离和勾股定理知识，设问指向能力立意评价.

从知识层面分析：学生已有解题经验是已知动点求线段和最小值问题，“最短路径”模型印象深刻.但本题反其道而行之，以线段和为条件，隐去“最值”关键词，将“最值”转化为“PM+PN=4”的条件，“4”是矩形的长，“4”也可以描述为平行线AB与CD之间的距离，初中阶段几何最值问题主要围绕“两点之间线段最短”“连接直线外一点与直线上点的所有线段中，垂线段最短”为知识基础，借助轴对称、平移、旋转等变换进行研究.点与点、点与线、点与形的关系是几何核心内容，定量确定特殊线，定性确定特殊点，从整体到局部，从一般到特殊，渗透、类比、化归、数形结合、特殊一般等数学思想，把不熟悉的数学问题转化为熟悉的问题.

从能力层面解析：试题在矩形中隐藏角平分线，构造等腰直角三角形，关注知识脉络，引导学生对题目信息进行深加工，通过“为形配数”和“赋形以数”，用数的精确性阐明形的对称性，依托形直观刻画“PM+PN=4”，构建直观模型实现“数”“形”的双向并进与融通，学生实现从“看到”到“想到”，学生感受到数形结合的“精妙”，在这个过程中，学生理性的几何直观和空间想象能力拾级而上，合乎逻辑的思维习惯、实事求是的理性精神得到有效培养，实现核心素养的落地.

从思维障碍探析：

1.学生没有发现ED=3的隐含结论.矩形图中隐含着Rt△EDC，线段CE是斜边也是∠BCD的平分线.当CE承担对称轴的作用时，可以实现PM+PN化折为直；当CE发挥角平分线的作用时，根据角平分线性质添加辅助线，构造“新的矩形”.Rt△EDC可以通过题中条件ED=3得到，也可以通过观察图形发现其特殊性.没有发现这个隐含条件，说明学生的“数感”“图感”经验有限.

2.学生对“最短路径”模型最深的印象是线段和最小，题目中没有给出“最小”关键词，导致无法调取解题模型和解题经验，说明学生模型的理解停留在“记忆再现”层级，并没有真正理解模型的本质与核心要素.

3.当学生看到PM+PN=4，从解题经验知道要化折为直，但对数字“4”不够灵敏，矩形长“4”隐含折直变换后恰与矩形边平行.对条件BN=BM不知如何使用.说明学生有问题线索的意识，但无法将多个信息点有机联系起来.

4.部分学生推理正确但运算失误，还有学生看到动点问题、看到这个题位即选择放弃.如果用爬山形容中考答卷，逾山望远山，峰峦叠翠，志强者智达.

几何最值问题的探究对学生数学思维，特别是创新能力的培养、核心素养的提升具有重要意义，考场上的“灵机一动”绝非轻易触动，它是完整的知识网络、扎实的推理功底、丰富的解题经验的综合体现.当题意理解透彻后，解题就进入了“模型”环节，图形由动变静，点线由多变少，有形的东西在消失，模型关键要素浮出水面，学生思维由几何直观过渡到图形抽象，由空间想象进入逻辑推理，分析问题、解决问题的能力一以贯之.思维障碍产生的原因有知识缺失，更是情感投入和意志力的支撑出现不足.四基四能让核心素养得以“丰腴”，敢于挑战、勇于克难、积极探索，丰富的情感投入让核心素养发展拥有核心动力.3  解法探究

解法1  模型驱动，合理构造

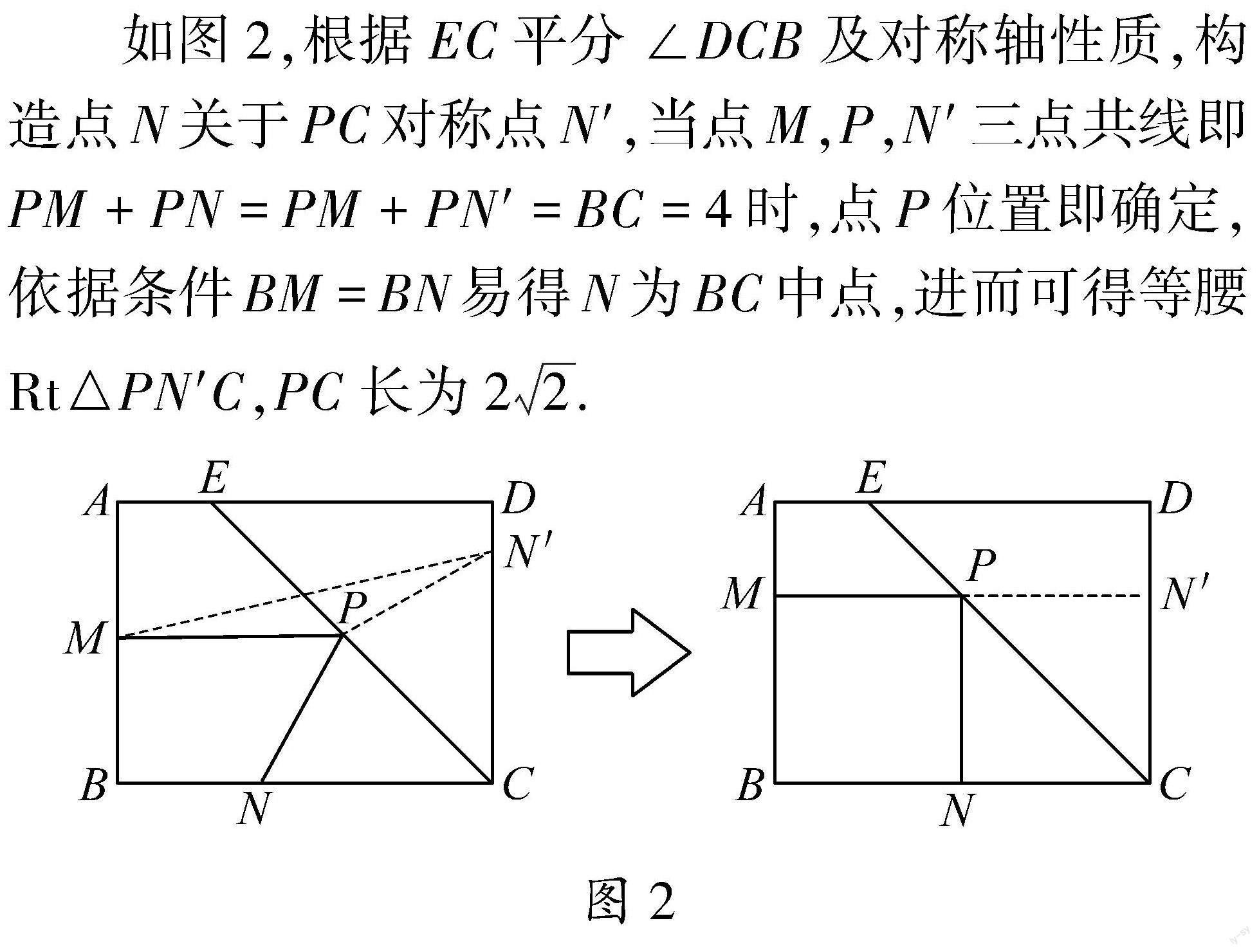
线段和常常在最短路径问题中出现，那么就需要判断“PM+PN=4”是不是最短路径.三角形三边关系隐含等量最值，轴对称性质实现共点线段化折为直，两大性质巧妙串联线段关系是破题的核心.BM=BN可以翻译为“线段BN绕点B逆时针旋转90°”，隐含邻边相等夹角为90°某特殊四边形的存在.EC既是∠BCD平分线，也是对称轴，当PN关于直线对称得到PN′时，PM+PN转化为PM+PN′，由“PM+PN=BC=4”即可判定“最短路径”模型.

如图2，根据EC平分∠DCB及对称轴性质，构造点N关于PC对称点N′，当点M，P，N′三点共线即PM+PN=PM+PN′=BC=4时，点P位置即确定，依据条件BM=BN易得N为BC中点，进而可得等腰Rt△PN′C，PC长为22.

解法2  研形理数，推理转能

动态几何中的线段和问题，问题虽为几何，但却赋予了“数”的特性，构建关联关系需要立足几何特征，把握几何性质，重点关注具有“数”属性的性质定理.如图3，根据BM=BN条件作垂直构造“特殊四边形”，由“PM+PN≥PQ+PR=BR+CR=BC=4”易证四边形PMBN为正方形，则PC=22.图3解法3  直觀蓄势，巧做智得  图4

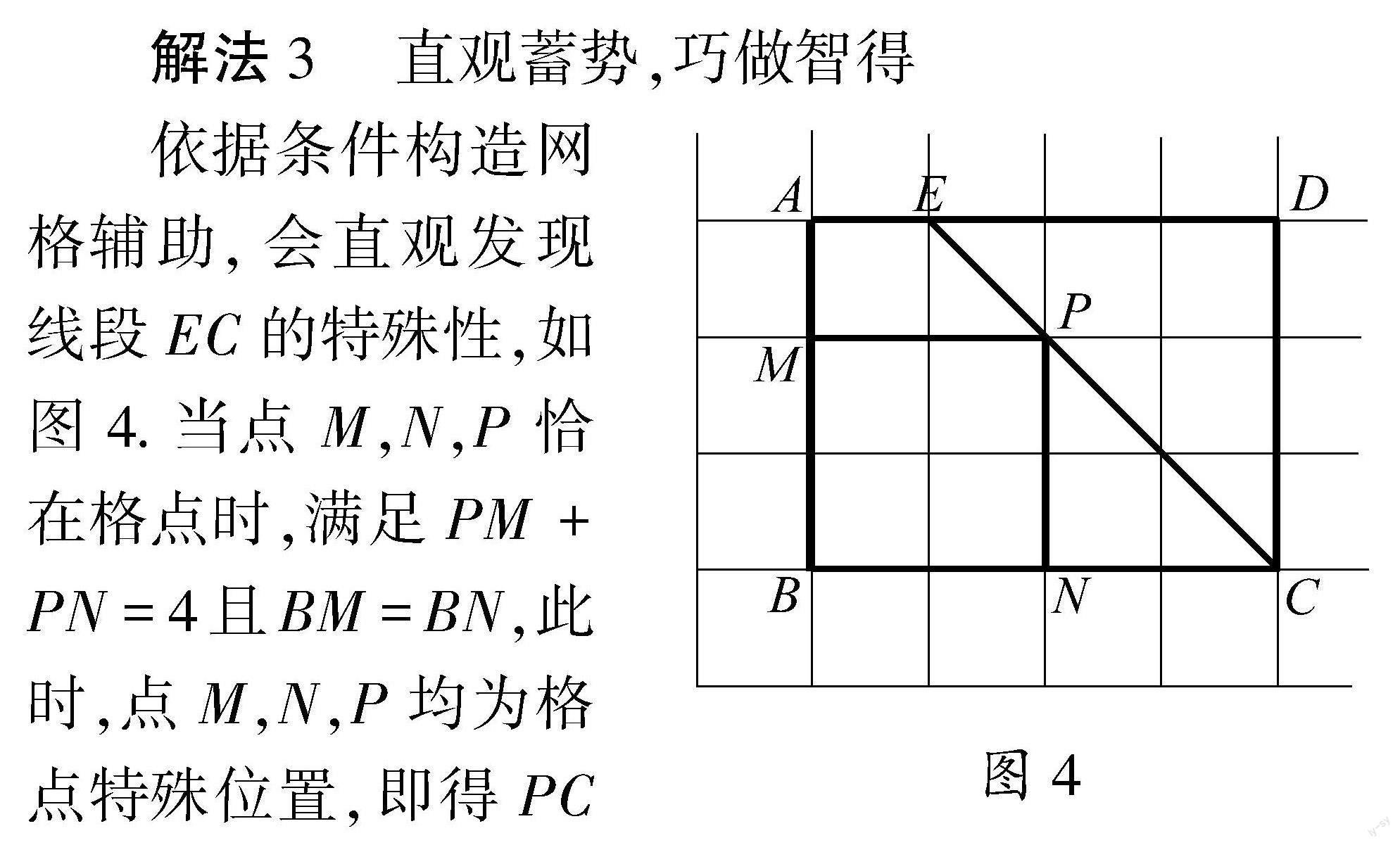
依据条件构造网格辅助，会直观发现线段EC的特殊性，如图4.当点M，N，P恰在格点时，满足PM+PN=4且BM=BN，此时，点M，N，P均为格点特殊位置，即得PC长.借助网格平行线、度量运算的内在力量，实现了填空小压轴的智得巧做.网格工具让条件中的数与量直观化，数与形真正结合，直观模型“再发现”让猜想可视化解题思路自然显现，网格工具增强推理意识，提升推理能力.

不同的解法隐含不同的思维路径，对条件的判断与认识程度，能够反应到做题繁简与用时差异，从而区分出不同层次的思维品质，测评出数学素养各要素的不同水平.解法3简洁明快，干净利落，网格作为非常态辅助工具，隐含建系策略，小格点大能量，为后续高中学习奠定坚实基础.4  真题“化”作业

中考题严格以课标为依据，紧紧围绕学科核心概念、思想方法、时代方向等命题，具有引导教学教研方向的重要作用.如果能够将中考真题分解转化为日常作业题组，针对知识考点和能力要求，将思维障碍进行分层分解，转换图形背景、变换问题设问、关联生活实际，精选精练精讲，就能够帮助学生真正走出题海，“作业”功能最大化.下面就以2023年陕西中考13题为例进行作业题组设计，作业目标、水平层级及学生自我评价量表［1］与每道题一一对应，学生通过题组训练，能够看到自我的进阶，实现从学会解题走向学会解决问题；老师也通过作业设计，更加明确教与学的方向，优化教与学的过程，用变式提高辩证、用“不变”策略激发应变活力.

4.1  作业目标

1.通过图形变化，强化识图、画图能力，渗透数形结合思想；

2.通过变化题设延伸结论，深化模型解题策略，提升化归能力；

3.通过解决实际问题，优化知识体系反思策略方法，培养思维审辩力.

4.2  水平层级

水平Ⅰ：加强记忆——复述强化，问题明确不再进行信息加工；

水平Ⅱ：再现方法——巩固所学方法解决学科内问题；

水平Ⅲ：熟练技能——强化技能，方法组合运用，知识综合应用；

水平Ⅳ：形成能力——能抽象出数学模型或探索内在规律，对问题进行数学化地分析、表达，能解决简单的实际问题或学科综合，形成自己解决问题的方法策略；

水平Ⅴ：培养思维——对不同背景下的过程性活动，能运用数学思维方式进行思考，能灵活运用思想方法解决问题，能进行扩展和延伸，展现理性思维.

4.3  学生自我评价量表

评价维度

优秀（3分）

良好（2分）

过关（1分）

再努力

1.读懂题意，能将图形与条件相结合

2.能读出题中隐含条件（由已知想可知）

3.能正确应用定理、性质

4.能根据题意构画辅助线

5.能找到这一类问题的共同特点（条件、图形、解法等）

6.能进行补图、变图、变条件、赋予实际背景并正确解答

4.4  作业题组设计

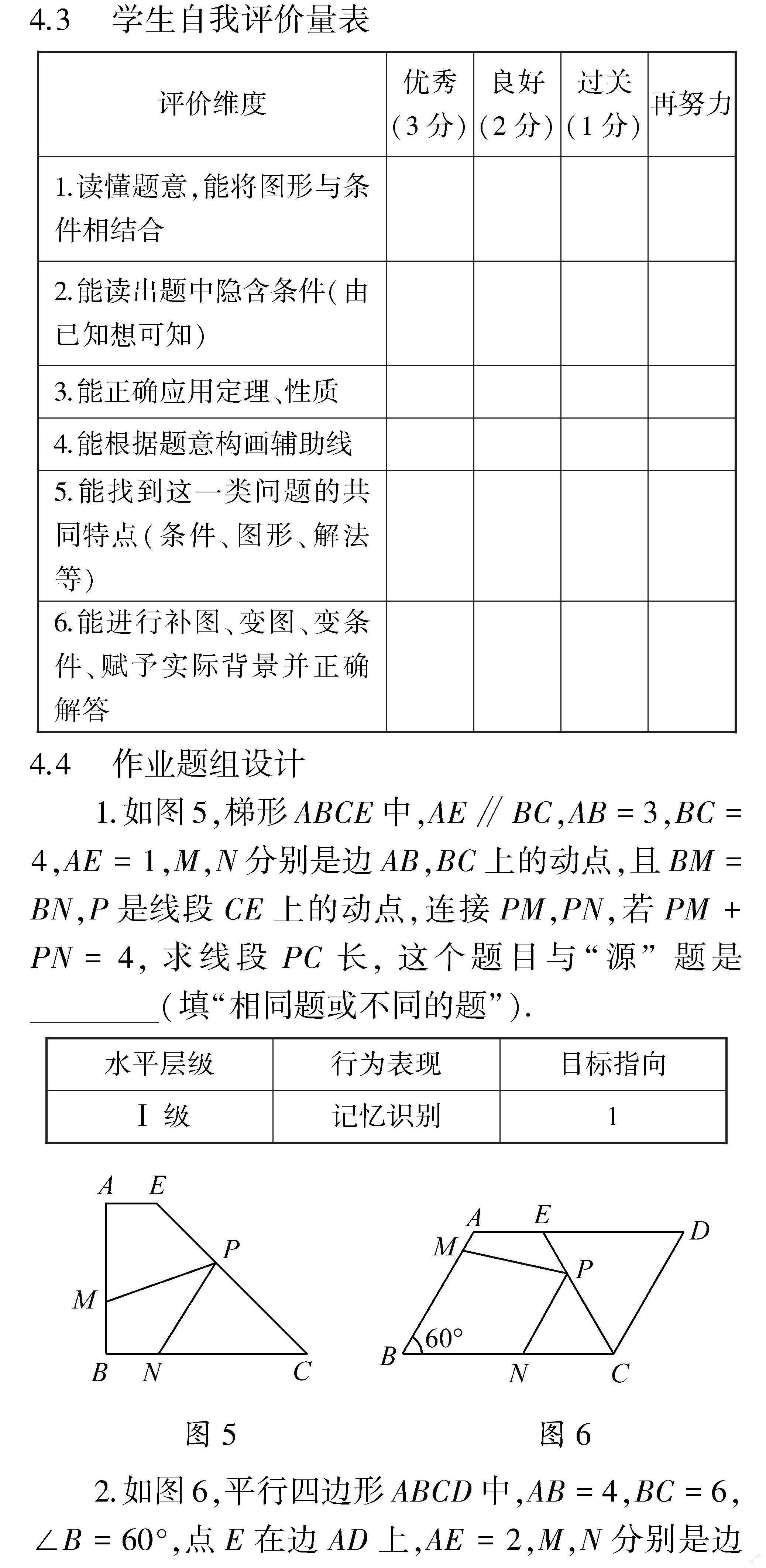
1.如图5，梯形ABCE中，AE∥BC，AB=3，BC=4，AE=1，M，N分别是边AB，BC上的动点，且BM=BN，P是线段CE上的动点，连接PM，PN，若PM+PN=4，求线段PC长，这个题目与“源”题是（填“相同题或不同的题”）.

水平层级行为表现目标指向

Ⅰ级记忆识别1

2.如图6，平行四边形ABCD中，AB=4，BC=6，∠B=60°，点E在边AD上，AE=2，M，N分别是边AB，BC上的动点，且BM=BN，P是EC上的点，若PM+PN=6，则线段PC长为.水平层级

行为表现

目标指向

Ⅱ级

理解初步应用

1，2

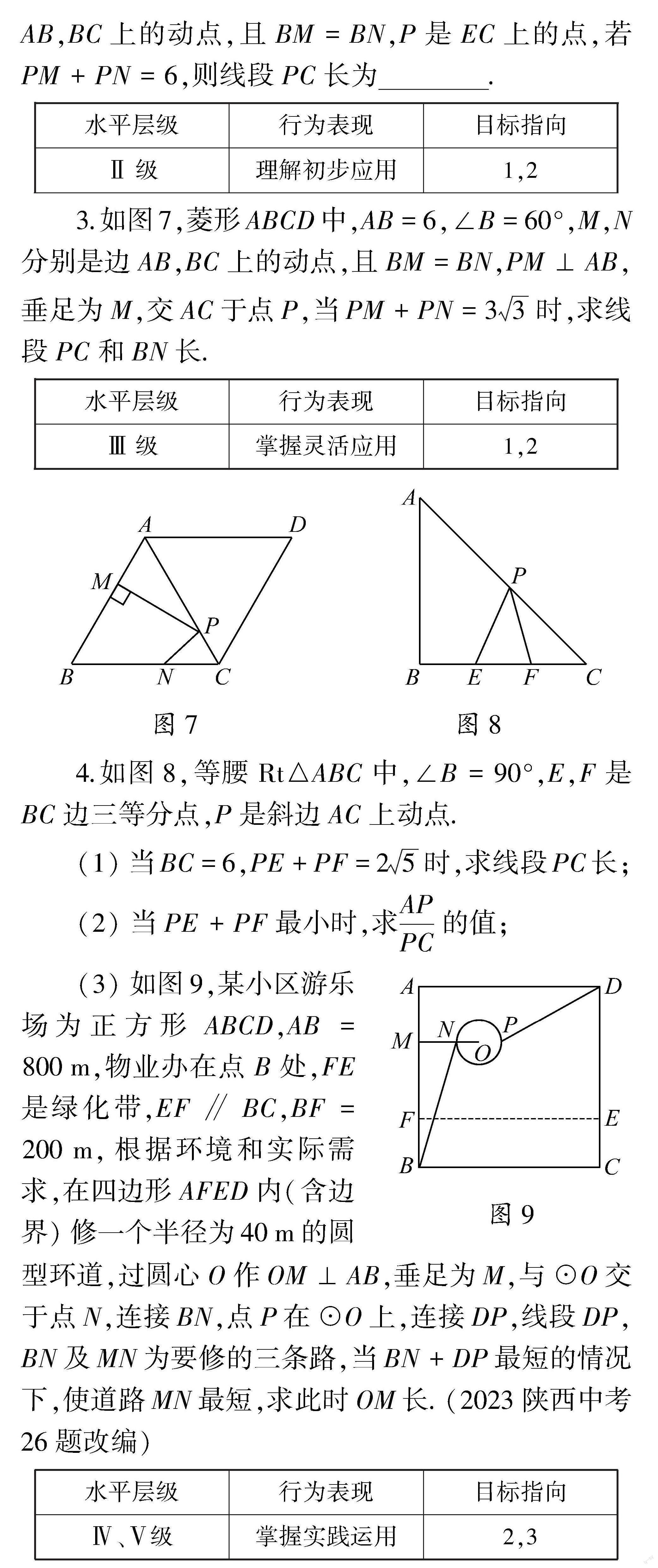
3.如图7，菱形ABCD中，AB=6，∠B=60°，M，N分别是边AB，BC上的动点，且BM=BN，PM⊥AB，垂足为M，交AC于点P，当PM+PN=33时，求线段PC和BN长.

水平层级行为表现目标指向

Ⅲ级掌握灵活应用1，2

4.如图8，等腰Rt△ABC中，∠B=90°，E，F是BC边三等分点，P是斜边AC上动点.

（1）当BC=6，PE+PF=25时，求线段PC长；

（2）当PE+PF最小时，求APPC的值；

（3）如图9，某小区游乐场为正方形ABCD，AB=800m，物业办在点B处，FE是绿化带，EF∥BC，BF=200m，根据环境和实际需求，在四边形AFED内（含边界）修一个半径为40m的圆型环道，过圆心O作OM⊥AB，垂足为M，与⊙O交于点N，连接BN，点P在⊙O上，连接DP，线段DP，BN及MN为要修的三条路，当BN+DP最短的情况下，使道路MN最短，求此时OM长.

（2023陕西中考26题改编）

水平层级行为表现目标指向

Ⅳ、Ⅴ级掌握实践运用2，35  教学启示

数学家华罗庚先生说：“数学是一个原则，无数内容，一种方法，到处可用.”经历中考复习后，大量的解题教学与训练，学生积累了丰富的解题经验，但为什么在考场上还会出现“纵使相逢仍不识”的现象？这就需要教师追溯“曾经相识”、找到“隐藏真相”、厘清本质核心，让解题“知其然、知其所以然、知何由以知其所以然”.

5.1  从雕刻试题到作业设计，让思维进阶

每年中考试题都是教研重要议题，小小试题承载着育人大使命和评价大任务，中考题中蕴含着最新研究方向、前沿研究领域、现有研究深度，试题从解答→解析→赏析，从三年学习进阶的视角去审视解题模型，从凝练经验形成策略去关注通性通法.试题也是作业，作业也是评价，作业融合“四基”“四能”和核心素养的主要表现，是阶段性评价的主要依据［2］.雕刻试题变作业设计，微雕强化记忆再现方法，浮雕凸显知识核心、渗透思想方法，3D圆雕综合应用素养落地.试题“分步得分”的本质是学生思维能力水平的层级划分，用作业评价量表让学生看到进阶之路，激活思维动力，久久为功步步踏实，实现思维进阶.

5.2  从赓续力量到技术赋能，助思维生长

审题阅读明“目标”，读图理数知“条件”，数形转化寻“路径”，反思回顾理“核心”.当解题与教学相遇时，解题就不再是以获得正确答案为目的.“数学+教育+网络画板”，用数学实验实现多维呈现，解决学生在“动态”问题中的“想不到、画不出、无感”情况，从具身体验到“离身”思辨，从“半脑”学习为全脑激活，实现了数学最核心能力“抽象”分层、分步.几何直观、逻辑推理同步整体提升.学生在探“变”究“核”中落下“数学印记”，老师在探“变”究“核”中从学科逻辑走向学习逻辑，让推理看得见，内化思维的“序”与“章”，同时也解决了不同学生思维进阶分层分步的“时差”问题.赓续力量技术赋能，师与生都是创生者，圆融无碍，应物无方，用教师的“思维深度”助学生的“思维生长”.

5.3  从核心概念到核心素养，育思维品质

平面几何研究基本图形构成元素及元素之间的关系，点就是基本元素，关系就在概念中.高中点与面、线与面、面与面位置关系的知识点，就是从初中点与点、点与线生长而来，从核心概念出发，对所习得的知识信息进行深加工，形成基件组块，用组块去建立能体现学科本质、对未来学习有支撑意义的结构化的网络体系，这个过程就是学生优化认知结构的过程，这个过程实现了从“学会数学思考”走向“通过数学学会思考”，用核心概念育可持續学习能力，携核心概念育高阶深度思维品质，引导学生运用所学数学知识从做题到做事，育人无声向素养.

参考文献

［1］王月芬.重构作业——课程视域下的单元作业［M］.北京：教育科学出版社，2022.1：197-198.

［2］中华人民共和国教育部.义务教育数学课程标准（2022版）［M］.北京：北京师范大学出版社，2022.4：3-4.

作者简介  刘英英（1974—），女，陕西西安人，中学高级教师，陕西省学科带头人;主要从事数学课堂教学研究;主持完成教育部子课题、省市规划课题，发表文章10余篇.