耿云玲， 刘中艳， 单庆晓

(国防科技大学 机电工程与自动化学院， 湖南 长沙 410073)

复数Daubichies小波的系统构造方法

耿云玲， 刘中艳， 单庆晓

(国防科技大学 机电工程与自动化学院， 湖南 长沙 410073)

摘要:从二带完全重构滤波器组的概念出发， 经理论推导提出了由实数Daubichies小波获得复数Daubichies小波的系统构造方法， 并通过实例验证了该方法的正确性. 在此基础上， 深入研究了最大正则阶条件下， 不同零点分布与复值滤波器及复值小波函数相应形式之间的关系， 给出了当最大正则阶分别取奇数和偶数时， 复值滤波器和复值小波函数在不同零点分布下的可能形式.

关键词:信号检测； 复数小波； 滤波器组； 核函数； 尺度函数

小波变换(Wavelet Transform)与Fourier变换的重要区别之一就是前者没有固定的核函数. 小波变换中核函数的这种不确定性一方面使得小波变换的结果强烈地依赖于所用小波函数的性质， 另一方面也为不断改善小波变换的结果提供了可能. 从这个意义上讲， 如何针对不同的问题来选取最佳小波函数应该始终是小波理论研究的一项重要课题[1-3]. 一般说来， 信号所具有的特征是通过其幅频特性和相频特性反映出来的， 因此对于本质上就是考察与信号局部相似程度的小波变换而言， 只有所用小波函数与被分析信号在幅频和相频上的匹配程度愈高时， 小波分析的效果才会愈好. 就目前广泛使用的各种实数小波来说， 由于其均不携带相位信息， 因此都难于做到这一点. 特别是除了Haar小波外， 现有实数小波大都不具有对称性， 这对保证小波变换的滤波特性具有线性相位， 在图像处理中对于避免移相都是非常不利的. 正是实数小波的这些不足， 促进了人们对复数小波的关注和研究[3-8].

到目前为止， 已有不少文献利用各种复数小波对工程实际问题进行了分析研究， 比如信号检测和分析等[1-3,7,8]， 其中个别文献也涉及到了复数小波的构造， 如基于幅频特性复值小波的构造、 提供方向选择性的同时还可提供近似移动不变性的双树复数小波的构造以及保证小波函数为对称的前提下又使其具有线性相位的复数双正交紧支小波的构造等[3-6,9-10]. 然而， 现有文献对如何通过理论推导系统地获得复数离散正交小波的方法均未涉及， 从而影响了其进一步的应用. 因此， 很有必要对此加以研究和探讨.

1二带完全重构滤波器组

自1992年， Vetteri M等在Mallat等建立的小波多分辨分析的基础上， 发现了小波在本质上就是满足一定特殊条件的完全重构滤波器组(Filter Banks， FB)后[10]， 在离散信号处理中的滤波器组理论和基于调和分析发展起来的小波理论之间建立起了紧密的联系. 从而使得利用FB理论对小波变换进行直观解释、 小波函数的构造以及小波变换应用范围的扩展等方面开辟了一条新的途径， 也为以FB理论为基础的各种新型小波的出现提供了可能和理论基础[11].

图 1　二带滤波器组Fig.1　Two-channel filter banks

图 1 所示为二带滤波器组FB. 其中：H0和H1分别为分解低通和高通滤波器， 而G0和G1则分别为重构低通和高通滤波器. 根据小波的紧支性要求， 这4个滤波器应均为因果的有限长数字滤波器； ↓2， ↑2分别代表下采样(抽取)和上采样(插值)， 且采样因子为2. 当图 1 中滤波器的系数分别为实数或复数时， 则分别对应实值或复值滤波器. 对比Mallat算法， 这里的H0和G0即为分解和重构尺度滤波器， 而H1和G1则为分解和重构小波滤波器. 在Z变换域， 图 1 实现完全重构FB的条件为[12]

(1)

(2)

式中：N表示滤波器的长度，c为一常数且满足|c|=1. 式(1)称为纯延时条件， 而式(2)则称为消除映象混叠条件. 为保证滤波器组为正交， 在复数域可设

(3)

(4)

(5)

式中： 上标“*”表示取共轭. 此时， 滤波器组中的4个滤波器的长度一致且均为偶数[10]. 由H1,G0和G1及式(1)可得

(6)

因此， 只要求得分解低通滤波器H0， 其他3个滤波器便可相应求出. 令

(7)

则有

(8)

需要明确的是， 离散正交小波基可导致完全重构FB， 而完全重构FB并不一定对应着一个离散正交小波基. 因此要保证由它获得离散正交小波基， 还需要对H0(z)施加一些限制. 即构造时， 除H0(z)为偶数长的FIR滤波器外， 还要满足[13]：

1)H0(z=1)=1.

(9)

若滤波器H0(Z)长为N， 则R(Z)是一阶次为(N-1-p)次的多项式. 且有

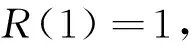
(10)

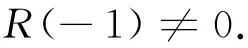
(11)

之后， 要通过迭代算法具体考察其收敛性， 即要求H0(z)应点收敛于一连续函数.P(z)的一般形式为

(12)

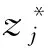
当H0(Z)为复值对称时， 对应的小波滤波器H1(Z)亦为复值对称的， 从而尺度函数和小波函数也均为复值对称.

2构造复数Daubichies小波

在实数离散正交小波中以Daubichies(db)系列小波的构造最为系统， 应用最为广泛. 如能系统解决从实数Daubichies小波来构造复数Daubichies小波的问题， 则可大大扩展复数离散正交小波的数目， 为不同问题的小波分析提供更多可供选择的复数离散正交小波函数.

引理 1复值正交对称尺度滤波器H0(Z)的零点必是互为倒数对.

证明当滤波器H0(Z)为正交对称时， 有

(13)

即

(14)

引理 2正交对称复值尺度滤波器H0(Z)的正则阶必为奇数.

证明将Z=-1带入式(14)， 有

(15)

由于N为偶数， 因此复数对称尺度滤波器在Z=-1处至少有一阶零点. 由式(9)可知， 当H0(Z)为对称时， 显然R(Z)也为对称的， 其阶数为N-1-p， 即

(16)

设H0(Z)的正则阶p为偶数， 而N-1-p为奇数， 则R(Z)在Z=-1处必有零点. 此时可将R(Z)表为

(17)

式中：R′(Z)的阶次为N-2-p. 因此，H0(Z)的正则阶必为奇数.

利用系数对称式(13)和H0(Z)的p阶正则两个条件， 通过求解式(8)， 在P(Z)可进行谱分解的情况下， 尽管能得到H0(Z)， 但当H0(Z)的长度较长时，P(Z)对应的为一高阶多项式， 其求解必然十分不便. 因此， 取代求解方程的方法， 利用引理1和引理2， 通过对已有实数Daubichies小波进行零点变换， 可方便地得到一系列复数的Daubichies小波.

(18)

而H0(Z)的长度

(19)

式中：N为偶数. 很显然， 要想从实数db小波得到复数db小波， 式(18)中的M≠0. 利用引理1， 在取最大正则阶的前提下(p=N/2)， 对式(18)中H0(Z)构成复值尺度滤波器时零点的分布情况作如下讨论：

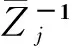
例如， 当p=3，N=6时， 由对应实数db小波按此法求解获得的其中一组对称复值滤波器(即对称复数尺度滤波器)H0(Z)的系数为：

2.712 75-1 044 389j1.864 05+3.502 14j-7.971 59+17.725 9j

-7.971 59+17.725 9j1.864 05+3.502 14j2.712 75-1.443 89j

其对应的尺度函数、 小波函数的实部(实线)及虚部(虚线)如图 2 所示.

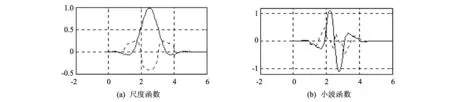
图 2　复数正交对称紧支db3小波Fig.2　Complex compactly-supported orthogonal and symmetrical db3 wavelet

2) 当p为奇数， 且K≠0. 由引理2知， 此时K必为偶数. 如果除Z=-1的实数零点外，

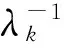
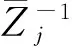
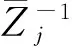
例如，p=4，N=8时， 求解获得的其中一组非对称正交复值滤波器H0(Z)的系数为

-0.065 449 483 946 584 08+0.056 034 386 820 235 545j

0.022 327 737 228 166 61+0.205 709 186 887 859 77j

0.591 993 187 857 351 9+0.206 458 492 528 848 04j

0.857 230 459 317 614 9-0.092 141 801 965 412 22j

0.246 276 641 390 715 56-0.280 171 934 101 177 9j

-0.193 976 174 460 788 74-0.131 995 745 315 530 16j

-0.065 713 564 114 935 59+0.017 679 054 752 094 2j

0.021 524 759 101 554 93+0.018 428 360 393 082 453j

其对应的尺度函数、 小波函数的实部(实线)及虚部(虚线)如图 3 所示.

图 3　复数正交非对称紧支db4小波Fig.3　Complex compactly-supported orthogonal and symmetrical db4 wavelet

在实数情况下， 当滤波器系数满足对称

(20)

或反对称

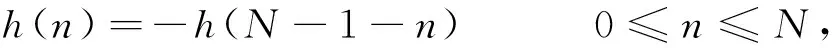
(21)

则此滤波器就具有线性相位的特性. 需要强调的是： 与实数时的情形不同， 在复数情况下， 滤波器或小波具有对称性质并不能保证它们是线性相位的， 此时线性相位成立的条件为[14]

(22)

或

(23)

同样在p=3，N=6时， 还可获得其中另一组复值滤波器H0的系数为

-0.095 560 1-0.050 862 8j 0.081 216 6-0.152 588j

0.721 45-0.101 726j0.721 45+0.101 726j

0.081 216 6+0.152 588j-0.095 560 1+0.050 862 8j

显然， 这组系数满足式(22)， 因此对应的小波既是正交对称的， 又是具有线性相位的， 由它得到的尺度函数和小波函数的实部(实线)和虚部(虚线)分别如图 4 所示.

图 4　具有线性相位的复数正交对称紧支db3小波Fig.4　Complex compactly-supported orthogonal and symmetrical db3 wavelet with linear phase

通过以上的分析可看出： 当p取最大正则阶N/2时， 若滤波器的长度为4m+2(m为整数)， 由式(8)有可能得到正交对称的复值滤波器H0(Z)， 但能否最终获得正交对称的复值滤波器H0(Z)还取决于H0(Z)中实数零点的分布情况. 而当滤波器的长度为4 m时， 由式(8)不可能得到正交对称的复值滤波器H0(Z). 这是由于前一种情况对应的p为奇数， 后一种情况则对应的p为偶数. 而p为偶数时， 由式(9)知， 此时R(Z)的阶次为奇数， 故H0(Z)除在Z=-1处有零点外， 肯定还有单个的实数零点存在. 因此在这种情况下， 可以考虑降低对H0(Z)正则阶的要求， 使R(Z)的阶数为偶数(即使p为奇数)以换来复值H0(Z)的对称性. 文献[15]提出了利用最小而完备的格型结构来设计具有任意长度、 任意正则阶的正交对称复值滤波器及小波的方法， 并给出了当滤波器长度分别为8和12时， 正则阶分别为1, 3和1, 3, 5所对应的复值对称尺度函数及小波函数.

表 1　不同正则阶对应复数离散正交小波函数的可能形式(p=N/2)

对以上讨论， 当式(18)中正则阶p=N/2取不同数值时， 对应复数离散正交小波函数的可能形式可由表 1 来总结. 由表 1 可知， 在最大正则阶的条件下， 复数正交对称小波的正则阶只能是奇数， 但正则阶为奇数时， 对应的复数正交小波并不一定是对称的； 而当正则阶为偶数时， 只能获得正交、 非对称的复数小波.

3结束语

在小波理论中， 小波函数的选取和构造是伴随其发展始终的问题之一. 本文从完全重构滤波器组出发， 通过理论分析， 提出了由实数Daubichies小波到复数Daubichies小波的系统构造方法， 为复数离散正交小波的构造提供了有益的方法. 特别是在复数域， 小波函数不仅可以是正交的， 而且还可以是对称的， 这可大大扩展小波变换的应用范围： 如利用复数小波的相位信息实现电网谐波检测等[16-18]. 近些年来， 对滤波器组的研究和对小波的研究一直是紧密相连、 相互促进的， 如多带小波的构造就是建立在多通道滤波器组的设计之上的. 总之， 基于滤波器组理论来研究新一代小波的构造以及快速算法的设计将成为当前小波理论发展的主要方向之一. 伴随而来可以肯定的是： 这些新一代小波在各种实际问题的求解中也必将获得更好的分析效果.

参考文献：

[1]周林， 夏雪， 万蕴杰. 基于小波变换的谐波测量方法综述[J]. 电工技术学报， 2006， 21(9)： 67-74.

Zhou Lin, Xia Xue, Wan Yunjie. Harmonic detection based on wavelet transform[J]. Transactions of China Electrotechnical Society, 2006, 21(9): 67-74. (in Chinese)

[2]王林泓， 陈学昌. 基于双密度双树小波变换的电能质量扰动识别方法[J]. 电测与仪表， 2012， 49(8)： 18-21， 26.

Wang Linhong, Chen Xuechang. Power quality disturbances identification based on double-density dual-tree discrete wavelet transform[J]. Electrical Measurement & Instrumentation, 2012, 49(8)： 18-21, 26.(in Chinese)

[3]黄群古， 任震， 黄雯莹. 基于幅频特性的复值小波构造及其在电力系统信号分析中的应用[J]. 继电器， 2001， 29(5)： 1-4.

Huang Qungu, Ren Zhen, Huang Wenying. The construct of complex wavelets based on amplitude-frequency characteristics and their application for fault signal analysis in power systems[J]. Relay, 2001, 29(5)： 1-4.(in Chinese)

[4]陈祥训， 淡文刚. 双正交紧支复小波的生成方法[J]. 中国电机工程学报， 2000， 20(4)： 87-92.

Chen Xiangxun, Dan Wengang. A lift approach to construct complex compactly-supported biorthogonal wavelets[J]. Proceedings of the CSEE, 2000, 20(4)： 87-92.(in Chinese)

[5]陈祥训， 淡文刚. 一种生成双正交紧支复小波的Lifting方法[J]. 中国电机工程学报， 2001， 21(5)： 34-37.

Chen Xiangxun, Dan Wengang. A generalization lifting approach to construct complex compactly-supported biorthogonal wavelets[J]. Proceedings of the CSEE, 2001, 21(5)： 34-37.(in Chinese)

[6]李佐胜， 姚建刚. 基于MAP估计的复小波域局部自适应绝缘子红外热像去噪方法[J]. 仪器仪表学报， 2009， 30(10)： 2070-2075.

Li Zuosheng, Yao Jiangang. Complex wavelet-domain local adaptive denoising method for insulator infrared thermal image based on MAP estimation[J]. Chinese Journal of Scientific Instrument, 2009, 30(10)： 2070-2075.(in Chinese)

[7]赵立权， 谢妮娜， 邬春明. Daubechies复小波的构造及在电能质量检测中的应用[J]. 计算机工程与应用， 2012， 48(5)： 233-237.

Zhao Liquan, Xie Nina, Wu Chunming. Construction of daubechies complex wavelets and application in power quality detection[J]. Computer Engineering and Applications, 2012, 48(5)： 233-237.(in Chinese)

[8]李涛， 何怡刚， 张宇. 基于提升小波的电能质量高效定位算法[J]. 仪器仪表学报， 2013， 34(2)： 281-288.

Li Tao, He Yigang, Zhang Yu. High efficient location algorithm for power quality signals with lifting wavelet transform[J]. Chinese Journal of Scientific Instrument, 2013, 34(2)： 281-288.(in Chinese)

[9]Kingsbury N G. Shift invariant properties of the dual-tree complex wavelet transform[C]. In： Proc. ICASSP. Phoenix, 1999, 16-19.

[10]Vetteri M, Herley C. Wavelets and filter banks： theory and design[J]. IEEE Trans on Signal Processing, 1992, 40(9)： 2207-2232.

[11]王红霞. 基于滤波器组的新型小波理论及其应用研究[D]. 长沙： 国防科技大学， 2004.

[12]宗孔德. 多抽样率信号处理[M]. 北京： 清华大学出版社， 1996.

[13]Daubichies I. Othonormal bases of compactly supported wavelets. Commun[J]. Pure Appl. Math. , 1988, XLI： 909-996.

[14]Zhang Xiaoping, Desai Mita D, Peng Yingning. Orthogonal complex filter banks and wavelets： some properties and design[J]. IEEE Trans on Signal Processing, 1999, 47(4)： 1039-1048.

[15]Gao XiqiQ, Nguyen Truong Q, Strang Gilbert. A study of two-channel complex-valued filter banks and wavelets with orthogonality and symmetry properties[J]. IEEE Trans Signal Processing, 2002, 50(4)： 824-834.

[16]赵成勇， 何明锋. 基于复小波变换相位信息的谐波检测算法[J]. 中国电机工程学报， 2005， 25(1)： 38-42.

Zhao Chengyong, He Mingfeng. A novel method for harmonics measurement using phase information of complex wavelet transform[J]. Proceedings of the CSEE, 2005, 25(1)： 38-42.(in Chinese)

[17]陈国志， 陈隆道， 蔡忠法. 近似线性相位复小波的电能质量扰动检测[J]. 电力系统及其自动化学报， 2009， 21(2)： 53-56.

Chen Guozhi, Chen Longdao, Cai Zhongfa. Power quality disturbance detection based on approximately linear phase complex wavelet[J]. Proceedings of the Chinese Society of Universities, 2009, 21(2)： 53-56.(in Chinese)

[18]冯洁， 周雒维， 刘毅. 基于复小波变换的暂态电能质量扰动检测与分类[J]. 电网技术， 2010， 34(3)： 91-95.

Feng Jie, Zhou Luowei, Liu Yi. Detection and classification of power quality disturbances based on complex wavelet transform[J]. Power System Technology, 2010, 34(3)： 91-95.(in Chinese)

Systematic Configuration of Complex Daubichies Wavelet

GENG Yunling， LIU Zhongyan， SHAN Qingxiao

(College of Mechatronics Engineering and Automation, National University of Defense and Technology, Changsha 410073, China)

Abstract:Proceeding from the two-band perfect reconstruction filter banks, a systematic constructing method deriving complex Daubichies wavelets from the real ones is proposed on the bases of theory and then the rightness of the method is tested by real examples. Next, the relationship between the different distribution of the zeros and the related forms of complex filters or complex wavelets is studied deeply under the largest rank of regularity. Last, the probably forms of complex filters and complex wavelets are presented when the largest rank of regularity is odd or even.

Key words:signal detection; complex wavelet; filter banks; kernel function; scale function

文章编号:1671-7449(2016)03-0185-06

*收稿日期:2015-12-17

基金项目：国家自然科学基金资助项目(51077046)

作者简介：耿云玲(1962-)， 女， 副教授， 博士， 主要从事电路理论、 电网电能质量分析、 小波变换及其应用等研究.

中图分类号:TM714

文献标识码:A

doi:10.3969/j.issn.1671-7449.2016.03.001