夏远梅,林安,赵克全

向量优化中改进集的一些拓扑性质

夏远梅,林安,赵克全

(重庆师范大学数学学院,重庆401331)

主要研究改进集的一些拓扑运算性质.首先在改进集条件下给出了拓扑向量空间中两个非空集之和的拓扑内部的一些运算性质.进一步,利用改进集获得了Flores-Baz´an和Hern´andez提出的假定B的一个加强形式.此外,给出了一些例子对主要结果进行了解释.

改进集;假定B;拓扑性质;向量优化

1 引言

文献[1-3]利用凸性假设给出了两个非空集合之和的拓扑内部的一些性质.这些性质在最优化理论及应用研究中是非常基本和重要的.因此,如何在其它一些假设条件下获得这些结果将是非常有意义的研究主题.为了处理数学经济问题,文献[4]引入了一类新的工具—free disposal集.基于comprehensive集的思想,文献[5]提出了改进集的概念并研究了它的一些性质.进而利用改进集定义了向量优化问题的一类统一的解—E-有效解,并建立了这类解的存在性定理.进一步,文献[6]将改进集的概念推广到了一般的实局部凸Hausdorf f拓扑向量空间.改进集与free disposal集之间具有密切的联系,它们在向量优化问题研究中扮演十分重要的角色[7-10].

受文献[1,3,6,8,11]中研究工作的启发,本文首先在改进集条件下获得了两个非空集之和的拓扑内部的一些运算性质.这些运算性质是对经典的凸性条件下相应结果的改进与推广.进一步,在改进集条件下获得了由Flores-Baz´an和Hern´andez提出的假定B的一个加强形式,给出了改进集的一个充分性条件.此外,提出了一些具体例子对主要结果进行了解释.

本文设Y是拓扑向量空间,K是Y中具有非空拓扑内部的凸锥,Rn是n维欧几里得空间,和分别表示非负象限锥和正象限锥.A是Y中的非空集合,cl A,int A和YA分别表示A的拓扑闭包,拓扑内部和补集.称A是关于K的free disposal集,若A+K=A[4].

下面,首先给出一些基本概念和引理.

引理1.1[1]设A和B是Y中的两个非空集合.如果int A/=∅,则int A+B⊂int(A+B).

定义1.1[5-6]设E是Y中的非空集合.如果0/∈E且E+K=E,则称E是关于K的改进集.

引理1.2[6]设E是Y中的非空集合.如果E是关于K的改进集,则int(cl E)=int E.

引理1.3[8]设E是Y中的非空集合.如果E是关于K的改进集,则int E=E+int K.

2 改进集之和的拓扑性质

基于Tanaka和Kuroiwa在文献[1,3]中的结果,给出改进集的一些拓扑内部性质.Tanaka和Kuroiwa在文献[1]中获得了下面的结果:

定理2.1设E1和E2是Y中具有非空拓扑内部的子集.如果E1和E2是凸集,则

注2.1如果E1和E2不是凸集,(1)式也可能成立.

例2.1令

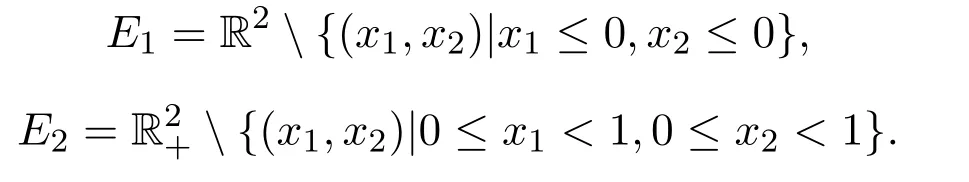
显然,E1和E2不是凸集.然而,int(E1+E2)=int E1+int E2=E1.即可以验证E1和E2是关于K=R2+的改进集.

下面利用改进集给出(1)式成立的一个新的充分条件.

定理2.2设K1和K2是Y中具有非空拓扑内部的闭凸锥,E1和E2是Y中的非空集合.如果E1和E2分别是关于K1和K2的改进集,则

(i)int(E1+E2)=int E1+int E2;(ii)int(E1+E2)=int E1+E2;

(iii)int(E1+E2)=int E1+cl E2.

证明只需证明(i)和(iii).因为E1和E2分别是关于K1和K2的改进集,所以

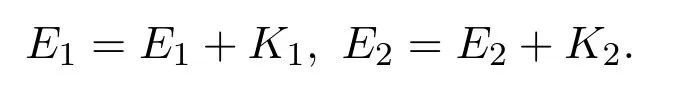
因此,E1+E2=E1+E2+K1+K2,即E1+E2是关于K1+K2的free disposal集.此外,由定理2.1可得int(K1+K2)=int K1+int K2.又由引理1.3,可知

又int E1+int E2⊂int E1+cl E2.由引理1.1可得,int E1+cl E2⊂int(E1+cl E2).再由文献[6]中的命题1.4(a)可得,cl E2是关于K2的free disposal集.因此,由(i)可得,

从而由引理1.2有int E1+int(cl E2)=int E1+int E2,即int E1+cl E2⊂int E1+int E2.

因此,int E1+int E2=int E1+cl E2.由(i)可得(iii)成立.

推论2.1设K1和K2是Y中具有非空拓扑内部的闭凸锥,E1和E2是Y中的非空集合.如果E1和E2分别是关于K1和K2的改进集,则

(i)int(E1+E2)=E1+int E2;(ii)int(E1+E2)=cl E1+int E2.

证明由定理2.2的证明过程可知结论成立.

Tanaka和Kuroiwa在文献[3]中获得了下面的结果:

定理2.3设E1和E2是Y中的子集.如果E1是具有非空拓扑内部的凸集,E2是开集,则int(E1+E2)=int E1+int E2.

注2.2如果E1是具有非空拓扑内部的凸集,E2不是开集,则定理2.3也可能成立.

例2.2令

显然,E1是具有非空拓扑内部的凸集,E2是闭集.然而,

下面,利用改进集提出(1)式成立的另一个充分条件.

定理2.4设E1和E2是Y中的两个非空集合.如果E1是具有非空拓扑内部的凸集,E2是关于K的改进集,则

(i)int(E1+E2)=int E1+int E2;(ii)int(E1+E2)=int E1+E2;

(iii)int(E1+E2)=int E1+cl E2.

证明仅需证明(i)和(iii).因为E2是关于K的改进集,所以E1+E2=E1+(E2+K),即E1+E2是关于K的free disposal集.从而由引理1.3可得,

因此,

下面,证明(iii)成立.显然,int E1+int E2⊂int E1+cl E2.此外,由文献[6]中的命题1.4(a),cl E2是关于K的free disposal集.从而由(i),引理1.1和引理1.2可得,

因此,int E1+int E2=int E1+cl E2.则由(i)可知(iii)成立.

定理2.5设E1和E2是Y中的非空集合.如果E1是开集,E2是关于K的改进集,则

(i)int(E1+E2)=int E1+int E2;(ii)int(E1+E2)=int E1+E2;

(iii)int(E1+E2)=int E1+cl E2.

证明仅需证明(i)和(iii).因为E2是关于K的改进集,由定理2.4的证明过程可知E1+E2是关于K的free disposal集.此外,由E1是开集和引理1.3可得,

下证(iii).显然,int E1+int E2⊂int E1+cl E2.由文献[6]中的命题1.4(a),(i)以及引理1.2可得,

从而由引理1.1可得,

因此,int E1+int E2=int E1+cl E2.从而由(i)可知(iii)成立.

注2.3如果E1不是关于K1的改进集,则定理2.2不一定成立;如果E1不是凸集,则定理2.4不一定成立;如果E1不是开集,则定理2.5不一定成立.下面的例子可以解释这一点.

例2.3令

显然,E1是非凸的拓扑闭集且不是关于K1的改进集,E2是关于K2的改进集.此外,

因此,

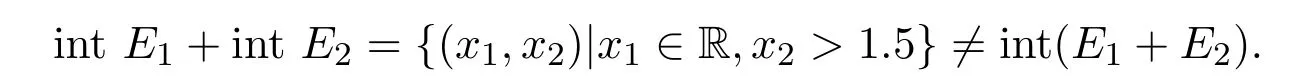
注2.4由前面的证明过程可知,关于K是改进集这一假设条件可以放松到关于K是free disposal集.

3 假定B的加强形式

Flores-Baz´an和Hern´andez在文献[11]中提出了假定B如下:

定理3.1设E是Y中的非空集合.如果E是关于K的改进集,则

证明仅需证明

可以验证int(Y(−int E))/=∅,即Y(−cl E)/=∅.若不然,Y(−cl E)=∅,则cl E=Y.利用引理1.2可得,int E=int(cl E)=int Y=Y.因此,E=Y,这与0/∈E矛盾.

下面,证明Y(−int E)是关于K的free disposal集.显然,Y(−int E)⊂Y(−int E)+K.因此只需证明:

若存在x∈Y(−int E)+K,x/∈Y(−int E).因为x∈Y(−int E)+K,则存在y∈Y(−int E)和z∈K,使得x=y+z.则y∈Y且−y/∈int E.由x/∈Y(−int E)可得x∈Y且−x∈int E.从而由文献[6]中的命题1.4(b),−y=−x+z∈int E+K=int E,矛盾.因此由引理1.3可得,

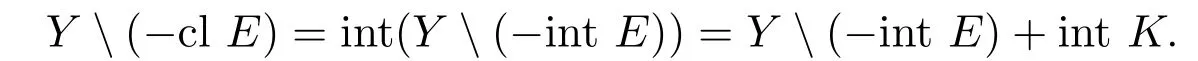
注3.1改进集蕴含假定B.事实上,只要固定q∈int K,由K是凸锥可知, Y(−int E)+R++q⊂Y(−int E)+int K=int(Y(−E)).

注3.2定理3.1的逆定理不一定成立.下面的例子可以解释这一点.

例3.1令

可以验证,

然而,

即E不是关于K的改进集.

定理3.2设E是Y中的非空集合.如果cl(Y(−E))+K=int Y(−E)且0/∈E,则E是关于K的改进集.

证明假设E不是改进集,则存在x∈E+K使得x/∈E.由x∈E+K可知,存在y∈E,即−y∈−E且z∈K,使得x=y+z.因为x/∈E,所以−x/∈−E.从而−x∈Y(−E)⊂cl(Y(−E)).因此,

这与−y∈−E矛盾.

[1]Tanaka T,Kuroiwa D.The convexity of A and B assures int A+B=int(A+B)[J].Applied Mathematics Letters,1993,6(1):83-86.

[2]Tanaka T,Kuroiwa D.Some general conditions assuring int A+B=int(A+B)[J].Applied Mathematics Letters,1993,6(3):51-53.

[3]Tanaka T,Kuroiwa D.Another observation on conditions assuring int A+B=int(A+B)[J].Applied Mathematics Letters,1994,7(1):19-22.

[4]Debreu G.Theory of Value[M].New York:John Wiley,1959.

[5]Chicco M,Mignanego F,Pusillo L,et al.Vector optimization problem via improvement sets[J].Journal of Optimization Theory and Applications,2011,150(3):516-529.

[6]Guti´errez C,Jim´enez B,Novo V.Improvement sets and vector optimization[J].European Journal of Operational Research,2012,223(2):304-311.

[7]Zhao Kequan,Yang Xinmin.A unif i ed stability result with perturbations in vector optimization[J].Optimization Letters,2013,7(8):1913-1919

[8]Zhao Kequan,Yang Xinmin.E-Benson proper efficiency in vector optimization[J].Optimization,2013,doi: 10.1080/02331934.2013.798321.

[9]Zhao Kequan,Yang Xinmin,Peng Jianwen.Weak E-optimal solution in vector optimization[J].Taiwanese Journal of Mathematics,2013,17(4):1287-1302.

[10]Zhao Kequan,Yang Xinmin.E-proper saddle points and E-proper duality in vector optimization with set-valued maps[J].Taiwanese Journal of Mathematics,2014,18(2):483-495.

[11]Flores-Baz´an F,Hern´andez E.A unif i ed vector optimization problem:complete scalarizations and applications[J].Optimization,2011,60(12):1399-1419.

Some topological properties of improvement sets in vector optimization

Xia Yuanmei,Lin An,Zhao Kequan
(College of Mathematics Science,Chongqing Normal University,Chongqing401331,China)

In this paper,topological operational properties of improvement sets are studied.Some operational characterizations of topological interior of sum for two nonempty sets are presented by using improvement sets in topological vector space.Furthermore,a strong version of Assumption B proposed by Flores-Baz´an and Hern´andez is obtained by improvement sets.Moreover,some examples are given to illustrate our main results.

improvement sets,assumption B,topological properties,vector optimization

O221.6

A

1008-5513(2014)06-0604-06

10.3969/j.issn.1008-5513.2014.06.009

2014-05-03.

国家自然科学基金(11301574,11271391,11171363).

夏远梅(1990-),硕士生,研究方向：最优化理论及应用.

2010 MSC:90C26,90C29,90C30