张晓明,姜金平,董超雨

KdV-Burgers-Kuramoto系统的渐近吸引子

张晓明,姜金平,董超雨

(延安大学数学与计算机科学学院,陕西延安716000)

研究了KdV-Burgers-Kuramoto方程的渐近吸引子,即利用正交分解法构造一个有限维解序列.首先用数学归纳法证明了该解序列不会远离方程的整体吸引子,接着证明解序列在长时间后无限趋于方程的整体吸引子,最后给出渐近吸引子的维数估计.

KdV-Burgers-Kuramoto方程;解序列;渐近吸引子;维数估计

1 引言

KdV方程是物理学中非常重要的一类非线性波动方程,已有许多研究[1-3],但对KdV的发展方程,如Benney方程解的研究相对较少,D.J.Benney研究了具有耗散和不稳定因素作用下的KdV方程,文献[2-4]提出了包含耗散和不稳定效应的一个重要的一维波产生模型Benney方程:

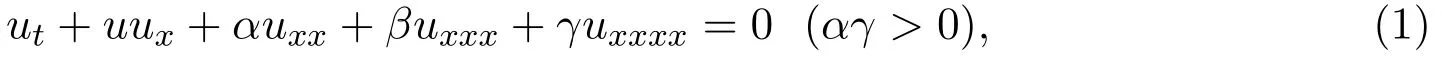
上式称为KdV-Burgers-Kuramoto方程.当β=1时称为Kuramoto-Sivashinsky-KdV方程[4],这个方程在等离子体物理、流体动力学和其他领域有着广泛的应用.

人们在研究无穷维动力系统学性质的过程中,相继建立了整体吸引子和惯性流形[5-6],将一个无穷维系统约化为一个有限维系统,但是要进一步研究约化后的有限维系统的动力学行为就显得很困难,因其结构是未知的,所以产生了近似惯性流形、指数吸引子和近似吸引子等概念[6-8],鉴于近似系统与原系统之间缺少较严格的等价性,文献[9]中提出了有限维渐近吸引子的概念.

定义1.1[9]对一个发展系统,其方程为:

记其相空间为H,解算子半群为{S(t),t≥0},吸收集为B.假设对任意u0∈B,存在N维子空间的近似解序列{uk(t),k≥1},满足:

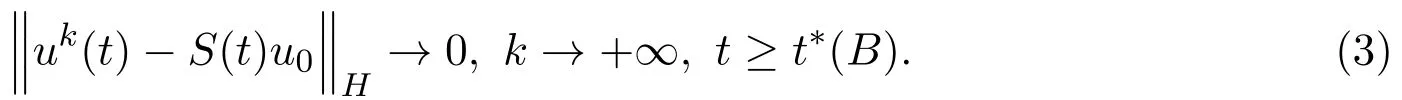
定义

为系统(2)的渐近吸引子,其中∥·∥H为相空间H的模,uk(t)依赖于初值u0,t∗(B)只依赖于吸引集半径,且对B中的u0是一致的.

因为uk(t)为N维系统的解,Ak的结构较易讨论,(3)式保证了uk(t)对真解u(t)的渐近逼近性而不仅是近似性.自渐近吸引子提出以来,一些方程的渐近吸引子已经获得[3,10-12].

本文将讨论一维周期边界条件下的KdV-Burgers-Kuramoto方程:

2 预备知识与解序列的构造

方程(4)-方程(7)的解的存在唯一性证明可参考文献[13],由此得到相空间([0,2π])和([0,2π])上的解算子半群{S(t),t≥0}.引入类似文献[14]有关吸收集的结论.

引理2.1对任意初值u0∈([0,2π]),若满足≤L(<∞),则存在时间

使得

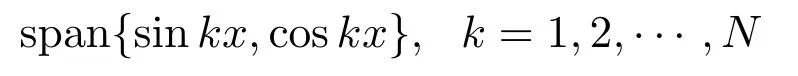
为HN,记([0,2π])到HN的N维正交投影为PN,而QN=I−PN.对

记p=PNu,q=QNu,则u=p+q,用正交投影可将方程分成两部分:

对任意初值u0(x)∈B,按如下方式构造渐近解序列:

3 逼近性证明

下面考虑渐近解序列uk(x,t)对精确解u(x,t)的逼近性.首先证明,对任意u0∈B,上述序列(11)-序列(12)所得的渐近解序列不会远离吸收集.

定理3.1设u(x,t)是对应于初值u0∈B的方程(4)-方程(7)的解,qk(k=0,1,2,···)按序列(11)-序列(12)给出,则存在N0∈N和(B),使得当N≥N0时,有

证明由吸收集的正不变性,u0∈B可得u(t)∈B,t≥0,则

为了证明(13)式,只需证明

即可.用归纳法证明,由q0与(11)式作内积得,

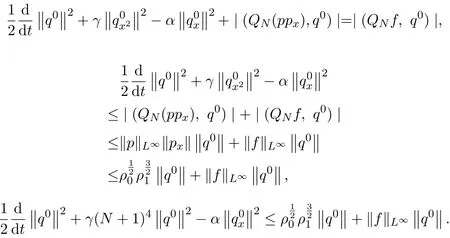
设E(N)=γN4−αN2,则有

即

所以,当N充分大,即满足

时,有

故由Gronwall不等式,存在

使得

即

当N充分大,满足

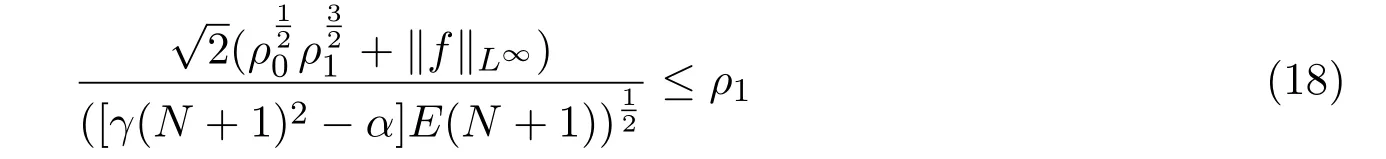
时,有

则由(17)式,(19)式可以说明当k=0时,(15)式成立.现在假设(16)式对k−1成立,即

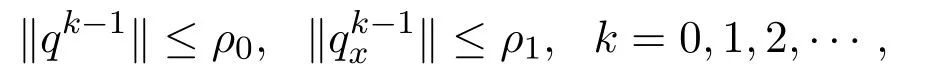
则由(12)式可得,

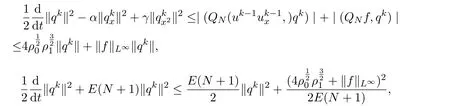
即

由Gronwall不等式知,存在

使得

即

所以,当N充分大时,满足

时,有

则

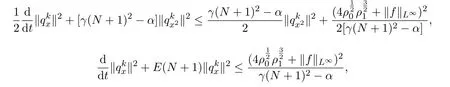
由Gronwall不等式知,存在时间

使得

即

当N充分大,满足

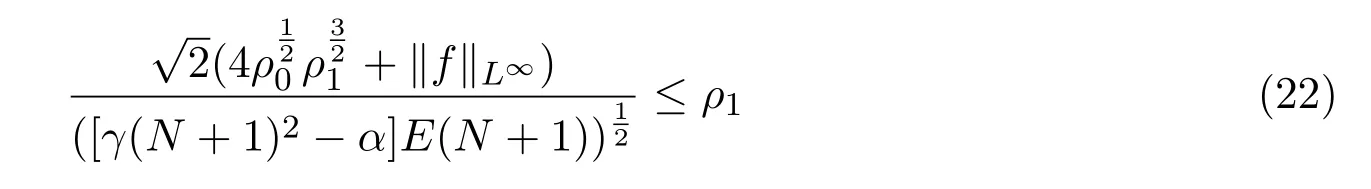
时,有

由(21)式,(23)式可知(15)式对k也成立,由归纳法原理可知,N0取满足(16)式,(18)式, (20)式,(22)式的最小自然数,=max{,,,},(15)式对一切k∈N成立.

下面证明qk收敛于q.

定理3.2设u(x,t)是对应初值u0的方程(4)-方程(7)的解,qk(k=0,1,2,···).由(11)式-(12)式给出,则存在N1∈N和t∗2(B)>0,使得当N≥N1时,有

其中N1为满足

的最小自然数.

证明记wk=qk−q,由(10)式和(12)式得:

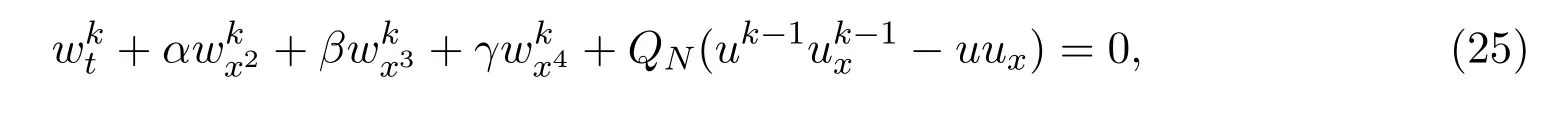
因为

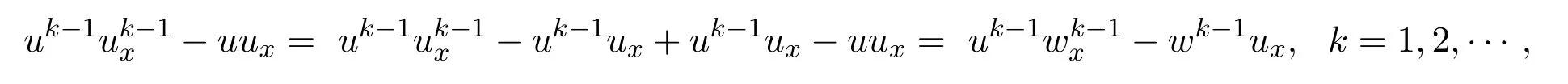
所以由(25)式得:

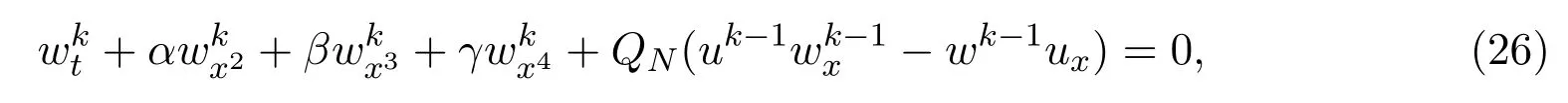
由(10)式和(11)式得:

从而

即

若要使∥wkx∥→0,k→∞,则需要取N1为满足

的最小自然数.

定理3.3设uk(x,t)为方程(11)-(12)的解,则

为方程(4)-方程(7)的渐近吸引子,且其维数即渐近解序列的维数为满足条件(20)式,(22)式, (32)式的最小自然数,即

[1]毛杰健,杨健荣.非线性KdV-Burgers-Kuramoto方程新的行波解[J].兰州理工大学学报:自然科学版, 2006,32(2):150-153.

[2]刘式适,刘式达.物理学中的非线性方程[M].北京:北京大学出版社,2000.

[3]罗宏,蒲志林,马丽蓉.耗散KDV型方程的渐近吸引子[J].四川大学学报:自然科学版,2009,46(6):1709-1713.

[4]Feng B F,Malomed B A,Kawahara T.Stable periodic waves in coupled Kuramoto-Sivashinsky-Kortewegdevries equations[J].J.Phys.Soc.Japan.,2002,71(11):2700-2707.

[5]Foias C,Sell G R,Temam R.Varites inertills des equations dif f erentielles dissipatives[J].C.R.Acad.Sci. Paris.Ser.I,1985,301:139-142.

[6]Temam R.Inf i nite-Dimensional Dynamical Systems in Mechanics and Physics[M].2nd ed,New York: Springer-Verlag,1997.

[7]Foias C,Manley O,Temam R.Sur linteraction des petits et grands tourbillon’s dans les ecoulements turblents[J].C.R.Acad.Sci.Paris Ser.I,1987,305:497-500.

[8]戴正德,郭柏灵.惯性流形与近似惯性流形[M].北京:科学出版社,2000.

[9]王冠香,刘曾荣.Kuramoto-Sivashinsky方程的渐近吸引子[J].应用数学学报,2000,23(3):329-336.

[10]邝雪松.四阶反应扩散方程的渐近吸引子[J].中山大学学报:自然科学版,2003,42(6):15-18.

[11]赵磊娜.一类非线性发展方程的渐近吸引子[J].重庆大学学报:自然科学版,2007,30(2):136-148.

[12]罗宏,蒲志林.Extended Fisher-Kolmogorov系统的渐近吸引子[J].纯粹数学与应用数学,2004,20(2):150-156. [13]马丽蓉.KdV-Burgers-Kuramoto系统的近似惯性流形[J].四川师范大学学报:自然科学版,2010,33(5):617-620.

[14]王冠香.一维周期边界条件下Kuramoto-Sivashinsky方程动力学初探[D].苏州:苏州大学图书馆,1996.

Asymptotic attractor of KdV-Burgers-Kuramoto equation

Zhang Xiaoming,Jiang Jinping,Dong Chaoyu
(College of Mathematics and Computer Science,Yan′an University,Yan′an716000,China)

In this paper,we study the asymptotic attractor of KdV-Burgers-Kuramoto equations.A solution sequence is constructed by using orthogonal decomposition.It is shown that the solution sequence doesn′t go away from the global attractor in terms of mathematical induction.Then it is obtained that the solution sequence approaches to the global attractor of the equation in long time and the dimensional estimate of the asymptotic attractor is obtained.

KdV-Burgers-Kuramoto equation,solution sequence,asymptotic attractor,dimensional estimate

O175.29

A

1008-5513(2014)06-0595-09

10.3969/j.issn.1008-5513.2014.06.008

2014-04-08.

国家自然科学基金(11171269);陕西省科技计划项目(2014K150307);延安市科技计划项目(2013KS03);延安大学研究生教育创新计划项目.

张晓明(1987-),硕士生,研究方向：无穷维动力系统.

2010 MSC:35B41