关于Kenichiro的一个丢番图方程问题
2014-07-24杨仕椿汤建钢吴莉
杨仕椿,汤建钢,吴莉
关于Kenichiro的一个丢番图方程问题
杨仕椿1,2,汤建钢2,吴莉2
(1.伊犁师范学院数学与统计学院,新疆伊宁835000;2.阿坝师范高等专科学校数学系,四川汶川623000)
研究了Kenichiro提出的轮换对称形式的丢番图方程,即方程的求解问题,利用素数整除的一些性质,证明了该方程仅有平凡解a=b=c以及非平凡解(a,b,c)=(k,k,4k),(k,4k,k),(4k,k,k)(k∈N),从而完全解决了这个方程.
丢番图方程;轮换对称形式;Kenichiro问题
1 引言
设N表示全体正整数的集合.关于轮换对称形式的丢番图方程,是一类基本而又重要的指数方程,它的求解问题一直是数论和组合研究中的有趣课题和困难问题[16]之一.例如,著名的Erd¨os方程,以及S´andon方程等[7-9].
文献[10]中,日本数学家Kenichiro提出了一系列尚未解决的问题和课题.他在该文献的第三章提出了14个问题,其中,问题13是四个丢番图方程的求解问题.最近,在文献[11]中,刘燕妮和郭晓艳完全解决了第一个丢番图方程,即xy+yz+zx=0的求解问题.而Kenichiro提出的第二个方程问题是:求方程

以及

的所有正整数解.并提出问题:方程(1),方程(2)是否仅有平凡解a=b和a=b=c?
在文献[12]中,Ding求出了方程(1)的全部正整数解以及方程(2)的部分正整数解.在该文献中,作者指出,方程(2)除平凡解a=b=c以及非平凡解(a,b,c)=(t,t,4t),(t,4t,t), (4t,t,t)(t∈N)之外,是否还有其它的正整数解,这是一个公开问题.
本文研究了不定方程(2)的求解问题,证明了该方程仅有正整数解a=b=c以及

在文末,对于方程(1),方程(2)的推广情形,提出了有待进一步研究的问题和猜想.
2 主要结果及证明
定理2.1方程(2)除正整数解(a,b,c)=(k,k,4k),(k,4k,k),(4k,k,k)(k∈N)之外,仅有平凡解a=b=c.
证明令gcd(a,b,c)=d,则可设a=a1d,b=b1d,c=c1d,且gcd(a1,b1,c1)=1,则方程(2)变形为:

因此只需考虑方程(2)当gcd(a,b,c)=1时的情形即可.
情形1a,b,c两两互素
若a>1,b>1,c>1,令标准分解式分别为:

其中α1···αr,β1···βs,γ1···γt≥1.
显然对任意1≤i≤r,1≤j≤s,1≤k≤t,均有

则由方程(2)可得,

于是由(3)式可得,

其中α=gcd(α1,···,αr),β=gcd(β1,···,βs),γ=gcd(γ1,···,γt).
如果α=1,则由(4)式可得,

于是

与β1≥1矛盾,则α>1.同理可得,β>1,γ>1.
若gcd(α,c)=1,则gcd(αb,c)=1,由(4)式的前两式可得,

于是,a+b+c≤3β,与β>1矛盾,则gcd(α,c)=d>1.令α=dα′,c=dc′,则gcd(α′,c′)=1.注意到gcd(a,c′)=1,则由(4)式的前两式可得,

于是a+b+c≤3dβ.由于d≤α,则

与α,β>1矛盾.因此,a,b,c中必然有一个为1.

则γ1=2,且r1=2,t=1,因此,c=4,此时方程(2)仅有非平凡解(a,b,c)=(1,1,4).设gcd(a,b,c)=k,则此时方程仅有正整数解

情形2a,b,c两两不互素
首先,不妨设a,b,c两两不互素.令

其中r1,···,rs,q1,···,qt,p1,···,pw为相异素数,且各指数λij≥1.于是,可令
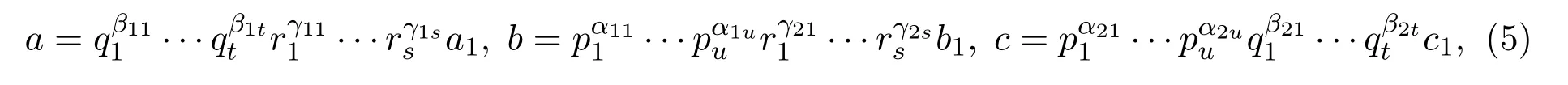
其中各指数均不小于1,且
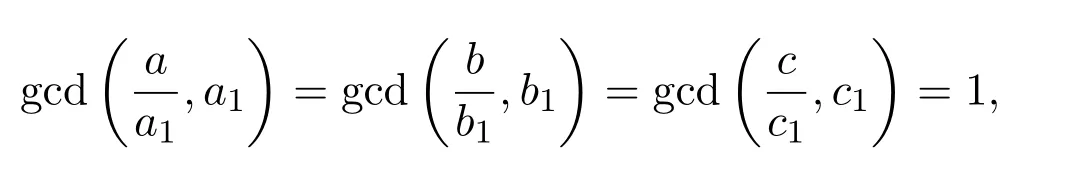
因此,a1,b1,c1两两互素.
如果a1>1,b1>1,c1>1,不妨设a1的标准分解式为则由方程(2)可得,(a+b+c)|3δjb(1≤j≤s).由情形1中a,b,c>1的类似讨论可得,矛盾,因此a1,b1,c1中必然有一个为1.
不妨设a1=1,c1>1,令c1的标准分解式为则由方程(2)可得, (a+b+c)|3δja.令

如果d>1,由于d|a,则存在qi或rj,使得qi|d或rj|d,则qi|b+c,于是qi|b,或者rj|c,均产生矛盾,因此d=1.由上式即可得,(a+b+c)|3δj,则a+b+c≤3δj,但与a≥2,b>2矛盾.于是,必然有a1=b1=c1=1.
在方程(2)中,考查a,b,c的标准分解表达式(5)中q1,···,qt的指数可得,


设gcd(a+b+c,a)=gcd(b+c,a)=d,如果d>1,由于d|a,同以上的方法,仍然可得矛盾,因此d=1.由上式即可得,(a+b+c)|3(β1lβ2j−β1jβ2l),则

但由于q1≥2,q2≥3,且当β1j,β1l,β2j,β2l≤5时,可直接验证上式不成立,则

于是利用不等式2x>2x2(x≥7)可得,


同理可令b=pα1rγ2,c=pα2qβ2,其中p,α1,α1,β2,γ2如上类似定义.于是由(6)式以及方程(2)可得,

由(7)式可得,
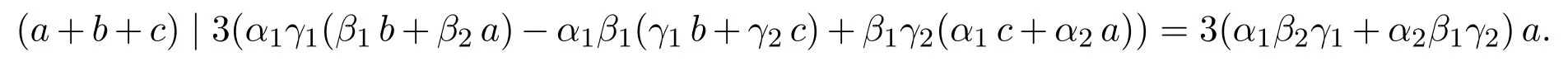
由于gcd(a+b+c,a)=gcd(b+c,a)=1,因此,a+b+c≤3(α1β2γ1+α2β1γ2),即

在(8)式中,不妨设p≥2,q≥3,r≥5,同理可直接验证,当α1,α2,β1,β2,γ1,γ2≤8时,(8)式不成立,则α1,α2,β1,β2,γ1,γ2≥9,于是利用不等式2x>x3(x≥10)可得,

与(8)式矛盾!因此,a,b,c中至少有两个数是互素的.
其次,由于gcd(a,b,c)=1,不妨设gcd(a,b)=d>1,gcd(a,c)=gcd(b,c)=1,则可令

且gcd(p1···pr,a1)=gcd(p1···pr,b1)=gcd(a1,b1)=1.如果a1>1,b1>1,c>1,由于a1,b1,c两两互素,则由情形1中a,b,c>1的类似讨论可得,矛盾,因此a1,b1,c中必然有一个为1.
若c>1,且a1=1,令考查c中的指数γj,由方程(2)可得,(a+b+c)|3γja.设gcd(a+b+c,a)=gcd(b+c,a)=d>1,由于d|a,则存在pj,使得pj|d,则pj|(b+c),即pj|c,这与gcd(a,b,c)=1矛盾,因此d=1.于是(a+b+c)|3γj,则(a+b+c)≤3γj,与γj≥1矛盾.若c>1,且b1=1,则a1>1,令a1的标准分解式为,则由方程(2)可得,(a+b+c)|3λjb.同样,由gcd(a+b+c,b)=gcd(a+c,b)=1可得,a+b+c≤3λj,可得出矛盾.
若c=1,当b1>1时,考查b1中的指数,由方程(2)同理可得出矛盾,则b1=1.同样,若a1>1,由方程(2)仍然可得出矛盾,则a1=1.因此,由方程(2)可得,(a+b+1)|3(αjb+βj),其中1≤j≤r.如果r>1,且存在j,l,使得则如同前面的类似讨论可得出矛盾,因此r=1,或者则可令a=pα,b=pβ,其中α=gcd(α1,···,αr),β=gcd(β1,···,βr),于是

如果α>β,则由(9)式可得,pα+pβ+1≤3(αpβ+β),则pα−β≤3α−1+3βp−β1≤3α.又由(9)式可得,

由于gcd(pα+pβ+1,pβ)=1,则(pα+pβ+1)|3(βpα−β−α+β),于是

由(9)式可得gcd(p,3)=1,由(10)式可解出p=2,max{α,β}<9,或p=4,max{α,β}<4,或p=5,max{α,β}<3,或p=7,α=β=1.再分别代入(9)式中一一验证可知,此时方程(2)没有正整数解.如果α≤β,则由(9)式可得,

由于gcd(pα+pβ+1,pα)=1,则由上式可得,

于是pα<3(β−α),或者pα 另一方面,由(9)式可得, 因此,pα+pβ+1≤3(αpα+α−β),则 由此可解出p=2,β≤9,或p=4,β≤3,或p=5,β≤2,或p=7,β=1,代入(9)式中一一验证可知,此时方程(2)也没有正整数解. 考虑方程(1),方程(2)的推广形式,即丢番图方程 由定理2.1证明的情形1类似可得: 推论3.1当n≥4时,方程(11)没有满足xi>1(1≤i)且xi,xj(1≤i,j≤n)两两互素的正整数解. 根据以上的讨论可知,当n≥4时,方程(11)的求解可能会变得较为麻烦,因此,一些自然的问题是: 问题3.1当n取何值时,方程(11)仅有平凡解x1=x2=···=xn? 问题3.2是否存在正整数n,使得方程(11)有x1>1,x2>1,···,xn>1的非平凡的本原解(即满足gcd(x1,x2,···,xn)=1)? 问题3.3方程(11)有x1 最后提出如下猜想: 猜想3.1当n=4时,方程(11)仅有非平凡的正整数解(x1,x2,x3,x4)=(k,k,4k,8k). 猜想3.2当n=5时,方程(11)仅有平凡解x1=x2=x3=x4=x5. 猜想3.3当n≥6时,方程(11)仅有有限个非平凡的本原正整数解. [1]Mordell L J.Diophantine Equations[M].London:Academic Press,1969. [2]Guy R K.Unssolved Problems in Number Theory[M].New York:Springer Verlag,2004. [3]Smarandache F.Only Problems,Not Solutions[M].Chicago:Xiquan Publishing House,1993. [4]Tom M A.Introduction to Analytic Number Theory[M].New York:Springer-Verlag,1976. [5]张文鹏.初等数论[M].西安:陕西师范大学出版社,2007. [6]潘承洞,潘承彪.素数定理的初等证明[M].上海:上海科学技术出版社,1988. [7]Chao K.Note on the diophantine equation xxyy=zz[J].J.Chinese Math.Soc.,1940,2:205-207. [8]Uchiyama S.On the Diophantine equation[J].Trudy Mat.Inst.Steklov.,1984,163:237-243. [10]Kenichiro K.Comments and Topics on Smarandache Notions and Problems[M].Erhus:Erhus University Press,1996. [11]刘燕妮,郭晓艳.一个丢番图方程及其它的整数解[J].数学学报,2010,53(5):853-856. [12]Ding Z S.Diophantine equations and their positive integer solutions[J].Scientia Magna,2007,3(4):77-80. A Diophantine equations problem by Kenichiro Yang Shichun1,2,Tang Jiangang1,Wu Li2 In this paper,we study a Diophantine equations by Kenichiro,that is the equationUsing some properties of prime number divisible,we proved that the equation have only positive integer solutions a=b=c and(a,b,c)=(k,k,4k),(k,4k,k),(4k,k,k)(k∈N).Thus,we completely solve the equation. Diophantine equations,rotation symmetrical form,Kenichiro problem O156.7 A 1008-5513(2014)06-0551-07 10.3969/j.issn.1008-5513.2014.06.001 2014-09-08. 国家自然科学基金(11301363);新疆维吾尔自治区普通高等学校重点学科经费(2012ZDXK21);四川省科技厅应用基础研究重点项目(2013JYZ003);阿坝师专重点科研基金(ASA14-09). 杨仕椿(1969-),硕士,教授,研究方向:数论及其应用. 2010 MSC:11D61,11A05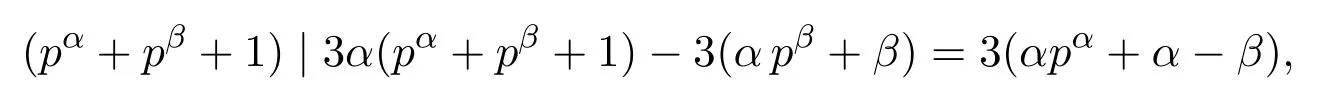

3 推论与进一步研究的问题

(1.College of Mathematics and Statistics,Yili Normal University,Yining835000,China; 2.Department of Mathematics,Aba Teachers College,Wenchuan623000,China)
