刘小树

安徽省蚌埠第二中学

文[1]中,详尽论述了圆锥曲线上不共线三点定理关于定点、定值的问题,提到了利用原点平移法解决复杂的计算.文[2]中,阐述了如何突破解析几何中的超量运算问题.两篇文章中均是研究如何破解解析几何中复杂运算的方法.然而最近几年高考中考查圆锥曲线定点、定值等问题,仍然是焦点,面对复杂的运算,如何将题目背景、考查思维方式分析透彻成为一种主流趋势.应用齐次化方法解决高考中圆锥曲线定点、定值等问题,应运产生.这是一种新型创新方法,倍受高考命题者和高中教师青睐,但一部分教育教学人员对此意义、使用原理存在疑问,了解不全面.因此,本文中尝试从基础知识开始讲起,结合例题,争取把齐次化方法的原理讲清楚.

1 预备基础知识

(2)对于二次曲线Ω:f(x,y)=Ax2+By2+Cxy+Dx+Ey+F=0(A2+B2≠0),文中主要考虑C=0,即f(x,y)=Ax2+By2+Dx+Ey+F=0(A2+B2≠0)的情形.

(3)直线方程有几种设法,用常数“1”代换,转化为二次齐次化方程.一般直线不过定点(x0,y0),如

λ(x-x0)+μ(y-y0)=1(λ,μ∈R).

①

再如y-y0=k0(x-x0)+m,即

②

(4)当直线方程代入二次曲线时,如何把方程齐次化?下面给出一般情况:

A[(x-x0)+x0]2+B[(y-y0)+y0]2+D·[(x-x0)+x0]·1+E[(y-y0)+y0]·1+F=0.

上式可化成

A(x-x0)2+B(y-y0)2+(2Ax0+D)(x-x0)·1+(2By0+E)(y-y0)·1=0.

③

④

2 典型例题应用

(1)求l的斜率;

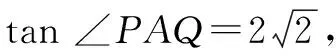
设直线l的方程为y=kx+m,则

⑤

平移后的双曲线方程整理为

2y2-x2+4x·1-4y·1=0.

⑥

把⑤代入⑥,齐次化为

设P(x1,y1),Q(x2,y2),则由韦达定理,得

解得k=-1.

(x-2)2-2(y-1)2+4(x-2)·1-4(y-1)·1=0.

⑦

直线l不过点A,设其方程为

m(x-2)+n(y-1)=1(m,n∈R).

⑧

把⑧代入⑦,得(4m+1)(x-2)2-(4n+2)·(y-1)2+(4n-4m)(x-2)(y-1)=0.

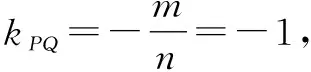
评注：2022年全国新高考数学卷中考查到定值问题即kPA+kAQ=0,则直线PQ斜率为定值.相对通法通解,利用齐次化法解决与直线斜率有关的定值、定点等问题很奏效,因此倍受关注.这种方法主要是绕过常规运用韦达定理比较复杂的运算,但实质还是使用代数的方法把和直线与曲线相交的点的斜率齐次化,使用齐次化后新的一元二次方程的韦达定理,本质上与原命题等价.这也体现了解析几何处理问题形式简捷、对称的数学美学思想.

下面再通过两个例题具体解释利用齐次化方法解决问题的详细过程和注意要素.

(1)求椭圆C的方程.

(2)若过点A作圆M:(x+1)2+y2=r2(r>0)的两条切线分别与椭圆相交于点B,D(不同于点A).当r变化时,试问直线BD是否过某个定点?若是,求出该定点;若不是,请说明理由.

(r2-1)k2+2k+r2-1=0.

⑨

⑩

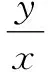
下面再看例题2,仔细体会.

(1)求轨迹E的方程,并说明轨迹表示什么图形?

(2)设过点A(0,-1)且斜率为k1的动直线与轨迹E交于C,D两点,且点B(0,2),直线BC,BD分别交圆x2+(y-1)2=1于异于点B的点P,Q,设直线PQ的斜率为k2,问是否存在实数λ,使得k2=λk1?若存在,求出λ值;若不存在,请说明理由.

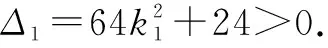
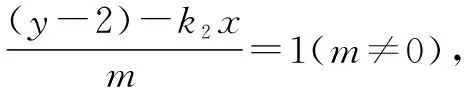
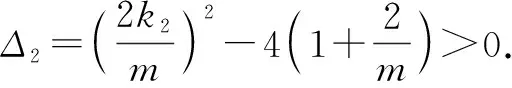
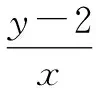
3 总结

齐次化构造一元二次方程,必须考虑二次项系数非零、判别式为正,保证后续运用韦达定理的正确性.对于二次系数为零的情况要注意讨论.这种方法的出现,既体现了命题者的智慧,也体现了答题者精巧、简捷的思维.而教育教学人员更是心有灵犀一点通,将命题与答题巧妙结合实施教学启发,进一步锤炼、加工,未来使齐次化方法变成新的通解通法.

利用齐次化方法解决直线与曲线相交问题中,定值、定点问题相对目前公认的通法通解来讲,运算过程易于把握,可减少出错的可能,但是新的方程下的使用也必须满足一元二次方程有两个不等实根.而对于圆锥曲线的其他问题,如点的坐标、线段、三角形、多边形面积的范围或最值等,就一筹莫展了.因此,通法通解有其广泛性.使用齐次化方法解决问题时,力求用好用准,同时注意问题的等价转化.随着高考改革的深入,伴随国家选用人才方式的调整转变,高考数学所考查的解题方式也发生着深刻变化,因循守旧、照本宣科行不通了.这需要我们数学教育教学工作者具有创新意识,在创新中解决新的变化,共同推进新时代背景下数学核心素养的发展新格局.