借助同课异构 提升教学效果
——以“函数的单调性”教学为例
2024-01-19高迎春
高迎春
江苏省高邮中学
在一次教学调研活动中,笔者很荣幸地观摩了两节关于“函数的单调性”的公开课.两位执教者是来自于两所不同学校的优秀教师,他们有着不同的教学风格.通过对比和反思,笔者收获良多,这里与大家分享了一些教学细节,谈一些自己的看法,以期抛砖引玉.
1 教学实录
1.1 情境引入
甲、乙两位教师都是把曲线图作为引入情境,试图借助图象让学生形成直观的认识.教师乙直接选择了教材案例——某天气温θ关于时间t的函数图象(图1);教师甲选择的是学生注意力指标数y随时间x的变化规律(图2).
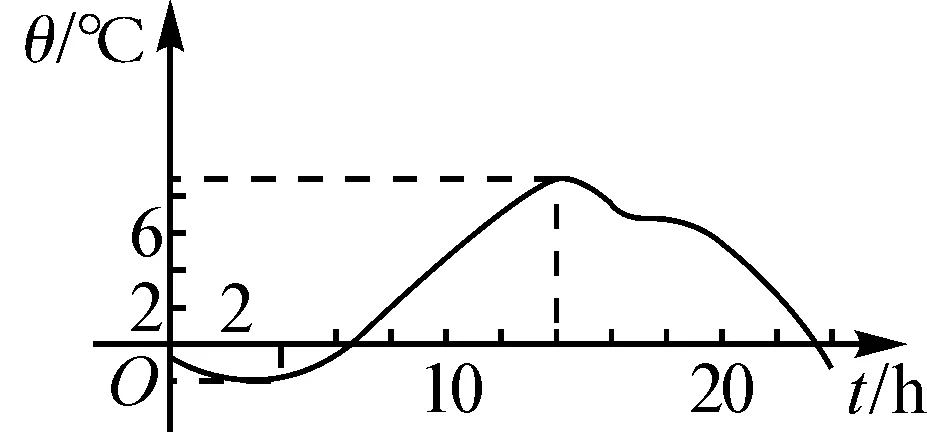
图1

图2
两位教师的情境内容都源于生活,符合学生的认知,能够快速地吸引学生的眼球,为后续的探究奠定了坚实的基础.相对而言,笔者认为教师甲的引入方案不仅简洁实用,而且新颖别致,更具目的性.众所周知,数学课堂时间有限,学生的注意力难以一直保持在一个最佳的状态,这就要求教师在情境引入阶段尽量地去除一些非数学信息的干扰,让学生迅速进入学习状态.从两张曲线图中清晰可见,图2更简洁,学生可以一眼就能看出变化趋势,而且学生可以准确地用数学语言来准确地表达这一变化规律.同时,图2也起到一个心理暗示的作用,让学生知晓在课堂上的注意力会随着时间的变化而变化,为了保证课堂效率,在关键节点要注意自我调节.与教师甲相比,教师乙的数据繁琐,图形曲线略显复杂,对未接触过单调性的学生来讲要求略高,若让学生直接描述变化规律,部分学生明显出现了信心不足.
1.2 概念构建
生1:在[0,10]内,y随着x的增大而增大;在[10,20]内,随着x的增大,y不变;在[20,45],y随着x的增大而减小.
师甲:表达得很清晰.如果用数学符号来体现这一关系,又该如何表达呢?(部分学生感觉无从入手.)
师甲:如果在[0,10]内取数,看看值有什么变化?
生2:在[0,10]内,取x1,x2,且x1
师甲:这样的x1,x2有没有要求?(学生并未作答.)
师甲:在这里应该要注意“任取”x1,x2,且x1 (d)The house in which I used to live has been knocked down. 从学生的反馈来看,师甲单调性概念的引入显得有些过急.其实学生对“任意”和“都”的理解对学生判断函数单调性是至关重要的,而从概念的形成过程来看,学生对这部分的自主探究较少,其主要源于教师的讲授,这样难以让学生形成深刻的印象,为此学生也很难应用概念去解决问题,显然这样的处理有些不妥.要知道,在初中阶段都是用静态数学符号去描述一些静态的数学对象,而高中阶段需要刻画动态的数学对象,学生难免会出现思维障碍.为此,教师在授课时要充分考虑学生思维能力的差异,舍得花时间帮助学生梳理,从而让学生学会用静态的符号语言去描述动态的数学对象. 基于此,笔者认为在概念生成前可以给出一些问题让学生去自主探究.问题如下: (1)在给定区间内取两个数,如1和2,满足f(2)>f(1),则函数f(x)是R上的增函数. (2)在给定区间内取5个数,如1,2,3,4,5,满足f(5)>f(4)>f(3)>f(2)>f(1),则函数f(x)是R上的增函数. (3)在给定区间取无数个数,如x1,x2,x3,……,xn,且x1 对于以上问题,教师可以引导学生先逐一思考验证,然后再从整体出发,由两个—多个—无数个,通过验证范围的不断扩大,引发学生对“无数”和“所有”的思考,从而为“所有”向“任意”的转变奠定基础.同时,概念的生成加入了学生的探究过程,有利于发展学生数学思维. 函数单调性的概念给出后,为了进一步理解概念、应用概念、强化概念,大多教师都会给出一些题目引导学生探究.两位教师同样采取了这样的教学策略,问题如下: 问题1判断下列说法是否正确: (1)定义在R上的函数f(x),满足f(2)>f(1),则函数f(x)是R上的增函数. (2)函数f(x)是R上的增函数,则f(2)>f(1). (3)定义在R上的函数f(x),满足f(2) (4)若定义在R上的函数f(x)在区间(-∞,0]上是单调增函数,在区间[0,+∞)上也是单调增函数,则函数f(x)在R上是单调增函数. (5)若定义在R上的函数f(x)在区间(-∞,0]上是单调增函数,在区间(0,+∞)上也是单调增函数,则函数f(x)在R上是单调增函数. 问题2结合函数图象写出下列函数的单调区间: 师甲给出概念后紧跟着让学生完成问题1,通过辨析来完成概念的理解和内化,之后通过问题2让学生结合函数图象寻找函数的单调区间.师乙先是引导学生观察图1,通过情境再现引导学生利用直观观察来寻找函数的单调区间.不过,学生利用图1寻找单调递增区间时,有的学生认为(7,14)是单调递增区间,显然这个区间偏小了,然而怎么让学生理解“偏小”?如何去“找大”呢?单调性本身就是函数的局部性质,那么选取局部区间为什么是不正确的呢?可见直接选取图1进行观察和辨析容易出现思路混乱,其实,教师可以选择问题1中的第(4)小问让学生体验何为“取大”,亦或让学生借助定义来判断效果更佳. 若两模块没有直接的联系,那么教师在完成教学内容时可以不考虑教学顺序,而本题中两个问题显然是存在联系的,为此在教学中先让学生应用概念判断函数单调性后再引导学生研究单调区间,效果更佳.其实数学是一门严谨的学科,逻辑性较强,数学结论的形成和发展都要有其严谨的理论依据.这就要求教师在日常教学中要摸清知识点间的逻辑关系,切勿因内容倒置而限制思维发展,挫伤学生学习信心.总之,教师要认真钻研教材,使得课堂教学更加连贯,衔接更加自然,进而培养学生良好的思维习惯和学习习惯. 生3:(-∞,0)∪(0,+∞). 师甲:这个答案大家认可吗?(学生沉思.) 师甲:如果答案不正确,你能给出正确的答案吗? 从课堂反馈上来看,很多学生与生3的答案一致,为此并未提出异议.而其正解为(-∞,0)和(0,+∞),由此可见学生认为“∪”与“和”等价.师甲反复强调二者的区别,并让学生举一些反例来验证.虽然教师千叮咛万嘱咐,然而在课后作业中发现,很多学生依然犯了错.其实,之所以教师刻意强调、叮嘱而学生依旧犯错,这与教师的提问方式有关.从教师的提问来看,已经暗示学生(-∞,0)∪(0,+∞)这个答案有问题,所以学生并未过多思考就给出了另外答案.学生对问题的认识不深,才会在课后作业中又出现问题.对于本题,教师可以给学生充足的时间去思考,充分去展现学生的思维过程,若此时教师再组织学生进行合作探究,学生一定可以自己发现问题.这样找到问题的症结后,问题自然迎刃而解. 其实,在本题探究后,教师可以组织学生重新审视问题1中的第(5)小问,这样学生自然能够理解何为局部性质,同时会明白,函数在不同区间内单调变化,并不能保证其在单调区间的并集上依然会递增或递减. 函数的单调性其实就是在某个区间内,函数所呈现的一定的变化规律,从图象上来看,就是代表一个变化趋势.本节课的教学重点是理解并掌握函数单调性的定义及掌握一些直观图形,对于函数单调性的相关证明,教师不应过于强求,要先保证学生能够跟得上之后再进行强化,切勿盲目求多而浪费学生独立思考和自主探究的宝贵时间.为保证课堂教学的质量,教师应多研究教材,研究课标,研究学生,从而通过适时、适量的问题来提高课堂效益. 两位教师的教学过程中虽然有一点瑕疵,然整体都很精彩,通过从“形”到“数”的分析和挖掘,不仅突出了教学重难点,而且关注学生自主探究与合作交流,凸显了学生的主体地位,取得了较好的学习效果. 其实,在教学中应多开展“同课异构”的教研活动,便于教师之间有更好的沟通和交流,进而取长补短,提高教师素养和教学水平.其实,同一教师在不同班级上课时也要注重“异构”,因不同班级的学生其认知水平和整体学习习惯也是存在一定差异的,通过“异构”可以打破“一刀切”的旧的教学模式,充分调动学生学习积极性. 总之,无论开展何种教学模式,其宗旨都是为了打造高效数学课堂.而高效离不开教师的引导和学生的自主探究,为此教师有必要为学生营造一个积极、自主、平等的学习环境,引导学生去发现、去探究、去感悟,进而实现高效数学课堂.1.3 概念辨析
1.4 练习讲评
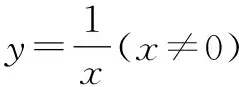
2 教学反思
