刘 鑫,张建影

(长春工业大学 数学与统计学院,长春 130012)

分数阶微积分方程是在传统微积分方程的基础上,用分数阶导数(积分)项代替传统微积分方程的时间或空间导数(积分)项.与整数阶方程相比,分数阶微积分方程在描述一些特殊问题时更有意义.例如: 多孔介质渗流问题[1];非牛顿流体的非局域性问题[2];描述地下水在非饱和土中的渗流过程[3];将分数阶方程与最优控制结合起来开发高效算法[4]等.但由于分数阶算子的特殊性,使得寻找分数阶微积分方程的精确解析解较困难.相比于求解精确解析解,数值解法更灵活,也适用于更多情况.目前关于分数阶微积分方程数值解的研究已有一定进展,例如: Mukhtar等[5]用Adomian分解变换方法和q-同伦分析变换方法,得到了分数阶方程多维模型的数值结果;Ali等[6]用最优同伦渐近方法推导出Caputo型分数阶导数的半解析解;Burqan等[7]利用Laplace变换和残差幂级数方法求解了分数阶方程的级数解.

时间分数阶方程是分数阶方程的重要分支,如何开发其数值算法目前已得到广泛关注.相比于宏观的有限差分方法,在求解时间分数阶微分方程时使用的复杂格式降低了算法的有效性.介于统计力学与流体力学之间的人工系统——格子Boltzmann模型,其更简单并适用于数值模拟.本文用格子Boltzmann方法(LBM)求解修正的时间序列分数阶方程.

1 基本理论

1.1 修正的时间分数阶扩散方程

考虑一个修正的时间分数阶扩散方程[8]:

(1)

(2)

1.2 对修正的时间分数阶扩散方程进行离散

整理可得

(4)

其中

1.3 格子Boltzmann模型

下面用格子Boltzmann方法恢复宏观方程.定义

(6)

这里fα(x,t)表示在时间为t、位置为x、速度为eα的粒子的分布函数,α为粒子速度方向.格子Boltzmann方程为

(7)

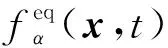
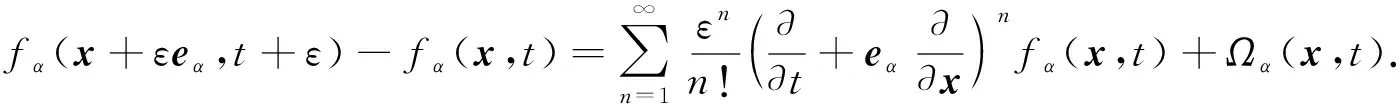
(8)

引入小Knudsen数ε,定义ε=l/L=Δt,其中l为平均自由程,L为宏观特征长度.在引入ε的情况下,对分布函数fα(x,t)进行Chapman-Enskog展开,有

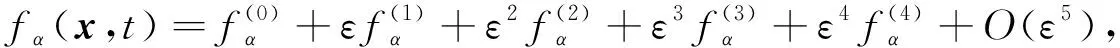
(9)

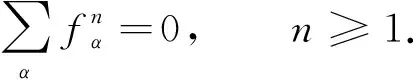
(10)

进行时间多尺度展开可得

t=t0+εt1+ε2t2+ε3t3+ε4t4+O(ε5),

(11)

从而有

(12)

源项有如下表达形式:

Ωα=εΩ1+ε2Ω2+ε3Ω3+ε4Ω4+O(ε5).

(13)

将式(8),(9),(11)～(13)代入式(7),并比较ε的各阶系数有

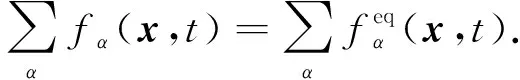
(16)

设源项满足如下条件:

平衡态分布函数满足:

(19)

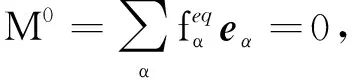
(20)

(21)

(22)

根据式(17)～(21)对式(22)进行整理,即可恢复出宏观方程

(23)

图1 D1Q3的格子模型Fig.1 Lattice model of D1Q3

这里＝－Dλεc2

下面推导平衡态分布函数.D1Q3的格子模型如图1所示.

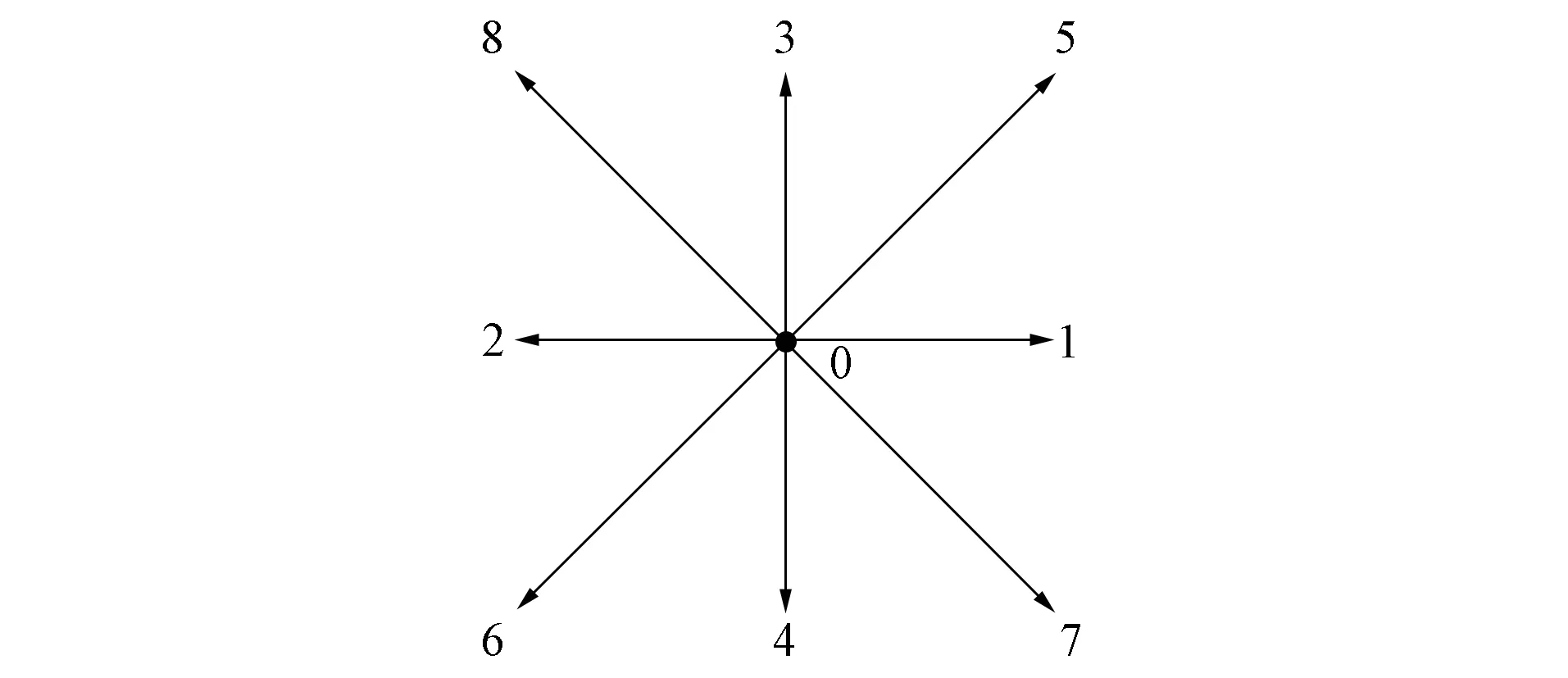
图2 D2Q9的格子模型Fig.2 Lattice model of D2Q9

根据式(19)～(21)可得平衡态分布函数为

(24)

(25)

其中c=|eα|是粒子沿各方向的移动速度.D2Q9的格子模型如图2所示.

同理可得平衡态分布函数为

2 数值计算

下面计算一个一维实例,因此所涉及的矢量x这里均为标量x.定义uN(xk,t)为数值解,uE(xk,t)为精确解.选择相对误差、最大绝对误差和全局相对误差进行验证,各误差表达式分别如下:

(29)

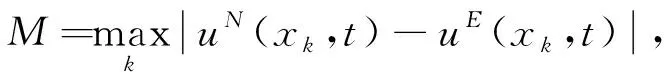
(30)

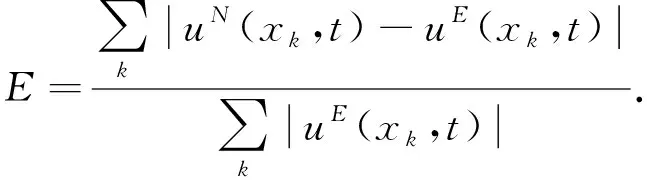
(31)

例1考虑带有如下初边值条件的时间分数阶方程:

(32)

方程(32)的源项为

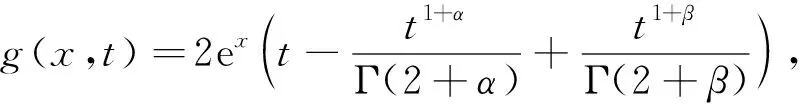
(33)

其精确解为

u(x,t)=t2ex.

(34)

图3 例1的数值计算结果(A)、误差分析(B)和收敛阶(C)Fig.3 Numerical calculation results (A),error analysis (B) and convergence order (C) of example 1

图3给出了例1的数值计算结果、误差分析和收敛阶.由图3(A)可见,数值解和精确解曲线吻合度较高,几乎完全重叠;由图3(B)可见,最大绝对误差为0.009 10,最大相对误差为0.004 52,两种误差都较小;由图3(C)可见,在一维情形下格子Boltzmann模型具有空间一阶收敛阶.

(35)

相对误差、最大绝对误差和全局相对误差的表达式如下:

例2考虑带有如下初边值条件的时间分数阶方程:

(39)

方程(39)的源项为

(40)

精确解为

u(x,y,t)=t2ex+y.

(41)

数值计算的参数选取: 时间步长和空间步长分别为

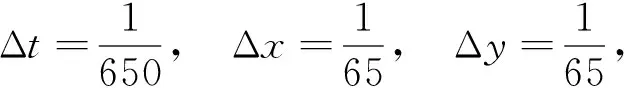
格子数为65×65,时间t=1.0,松弛因子τ=1.25,分数阶取值为β=0.001,α=0.001,扩散系数为D=0.001.

图4 例2的数值计算结果(A),(B)、误差分析(C)和收敛阶(D)Fig.4 Numerical calculation results (A),(B),error analysis (C) and convergence order (D) of example 2

图4给出了例2的二维数值计算结果、误差分析和收敛阶.由图4(A),(B)可见,方程(39)的数值解和精确解基本一致;由图4(C)可见,最大相对误差是0.012 2,最大绝对误差是0.009 06;由图4(D)可见,在二维情形下格子Boltzmann模型具有空间一阶精度.

综上所述,本文基于格子Boltzmann方法,针对修正的时间分数阶方程进行了讨论.首先将方程离散化处理,得到了标准的反应扩散方程.其次,根据Taylor展开式和Chapman-Enskog多尺度展开等技术,用格子Boltzmann方法准确地恢复了宏观方程,并推导出各方向的平衡态分布函数表达式.最后,用一个一维实例和一个二维实例进行数值计算,所得数值解与精确解吻合较好,误差在合理范围内.因此,格子Boltzmann模型在求解修正的时间分数阶方程的数值解上效果较好.