季鑫缘,董建涛,陶 浩

(1.西安电子科技大学 数学与统计学院,西安 710126;2.中电科思仪科技股份有限公司,山东 青岛 266555;3.西安电子科技大学 网络与信息安全学院,西安 710126)

期权定价是金融数学和金融工程领域的研究热点,研究期权价格的建模和计算方法对于理解期权价格走势、创造新的金融工具及评估与特定期权相关的风险至关重要.经典Black-Scholes模型[1]作为期权定价的基础,先假设资产回报率和波动率均为常数,然后通过风险中性等价鞅测度下的折现计算期权价格.基于Black-Scholes模型,可以计算出期权价格的封闭式解.但Black-Scholes模型在实际计算期权价格时表现不佳[2].例如: Black-Scholes模型假设无交易成本,但事实上交易时存在手续费;Black-Scholes模型中假设波动率和无风险利率为常数,但事实上它们通常是不固定的.

目前,数据密集型的机器学习方法已广泛应用于医疗保健、教育、制造和金融建模等领域.作为机器学习的重要组成部分,深度学习方法比传统的机器学习方法更适应高维、非线性的复杂数据[3],但解决此类问题通常需要以大型数据集为依托,而获取大量的期权价格数据用于神经网络的训练又需要非常高的成本.因此,本文考虑将深度学习与随机微分方程(SDE)相结合,把Black-Scholes模型中的漂移项和扩散项参数化为神经网络,既保留SDE的一般结构,又通过SDE的约束减少训练神经网络所需的数据.通过选取真实的日后复权股票价格数据作为训练集和测试集进行实验,经过反向传播不断更新网络的权重使训练损失收敛,最终得到的网络在预测股票价格方面具有更高的准确度,进而实现对期权更准确的定价.

对于一个目标期权的价格,在每个时刻股票价格数据不可观测时,无法再通过神经随机微分方程(NSDE)的方法对其进行学习.由于目标期权和已知股票价格的期权都可以用其风险中性等价鞅测度表示,因此本文考虑把目标期权价格和一个已知期权价格的差值限制在它们的Wasserstein距离内,以实现对期权价格的估计.

1 模型建立

1.1 建立神经随机微分方程模型

设(Ω,F,P,F=(Ft)t≥0)为一个过滤概率空间,其中过滤 F=(Ft)t≥0满足通常条件,B=(Bt)t≥0为该概率空间下的一个标准布朗运动.假设股票价格过程(St)t≥0满足如下随机微分方程:

dSt=μStdt+σStdBt,

(1)

其中回报率μ∈,波动率σ>0.实际应用中,回报率和波动率通常很难估计,尤其是回报率μ.因此本文采用NSDE的方法估计回报率和波动率,下面假设和分别为NSDE的漂移参数和波动参数,即NSDE可表述为

(2)

其中St表示由NSDE得到的t时刻的股票价格,θμ和θσ分别表示深度学习中未知的权重和偏移参数.

则对任一初始值X0∈,NSDE存在唯一强解.

假设以某支股票为标的资产的期权合约到期日为T,则对于t∈[0,T],可将式(1)写成如下积分形式:

(3)

St=S0exp{σBt+(μ-σ2/2)t}.

(4)

进一步,假设 Q表示与自然概率测度 P等价的风险中性等价鞅测度,则由资产定价第二基本定理可知,在无套利条件下,与 P等价的风险中性等价鞅测度存在且唯一[5].在测度Q下,贴现过程是鞅,本文以欧式看涨期权为例,其他类型的期权可用类似的方法建模和分析.根据Girsanov定理,BQt表示测度Q下的标准布朗运动:

BQt=Bt+κt,

其中κ=(μ-r)/σ表示风险的市场价格,r为无风险收益率[6].欧式看涨期权在0时刻的价格可表示为

P0=EQ[e-rTφ(ST)],

(5)

其中φ(ST)=(ST-K)+,K为行权价格,φ(·)为正部函数.下面通过测度变换技术,将定义在测度 Q下的欧式看涨期权价格重新表示为在自然概率测度 P下的表达式.

引理2若以式(1)中的St作为欧式看涨期权标的股票的价格,则该欧式看涨期权在0时刻的价格可表示为

(6)

其中t∈[0,T].特别地,对于零利率(r=0),有

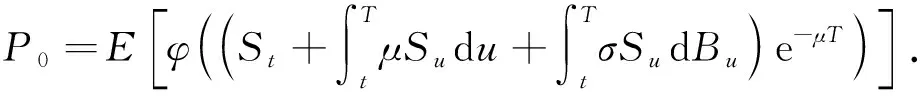
(7)

证明: 由式(4)得

将κ=(μ-r)/σ代入式(8)并化简,得

(9)

将式(3)代入式(9),并展开ST项即可证明式(6).证毕.

(10)

特别地,当r=0时可将式(10)化简为

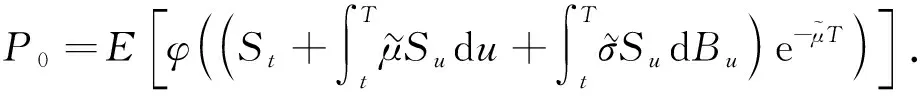
(11)

1.2 构建网络结构

对于估计μ,建立含有3个隐含层的简单神经网络训练参数μ,其中θμ=(Wμ,bμ)为漂移网络的权重矩阵和偏移参数.对于估计σ,建立包含4个隐含层的神经网络训练参数σ,其中θσ=(Wσ,bσ)表示扩散网络的权重矩阵和偏移参数[7].设两个网络中每个隐含层的节点数均为100个,分别建立如图1所示的网络结构.

图1 神经网络结构Fig.1 Structure of neural network

(12)

图2 Tanh激活函数及其导函数图像Fig.2 Tanh activation function and itsderivative function images

Tanh激活函数图像如图2所示.考虑将式(2)随机微分方程的解离散化表示,将时间区间[0,T]等间距划分为N份,当时间间隔足够小时,股票价格过程有如下迭代形式[8]:

图3 NSDE结构Fig.3 Structure of NSDE

2 实证分析

2.1 训练神经随机微分方程模型

图4 股票价格数据Fig.4 Stock price data

实验选取真实的股票价格数据作为输入,以图4中2012—2015年的958个交易日的日后复权股票价格数据为训练集,2016年的前200个交易日的日后复权股票价格数据为测试集,以训练后t时刻的股票价格作为网络的输出项.在标的资产为单一股票的情形下,在神经网络前向传播的过程中,输入层将初始价格数据传输至隐藏层,通过梯度下降不断训练漂移和扩散参数,最终在输出层通过激活函数得到模拟的股票价格数据.

训练算法的过程实际是通过每次迭代后计算损失,然后交替更新漂移网络与扩散网络中的参数.Zhou等[9]研究表明,损失函数在神经网络模型的训练中具有重要作用,神经网络的精度通常也受损失函数的限制.在深度学习的回归问题中,通常可选择均方误差 (MSE) 或平均绝对误差(MAE) 作为训练的损失函数,考虑到使用MAE函数训练收敛速度较慢,为保持模型的整体性能,本文选择用MSE函数计算损失[10].由于股票价格走势是非凸函数,因此对网络权重的更新采用随机梯度下降法.Hardt等[11]研究表明,虽然随机梯度下降法在解决非凸函数的优化问题上没有理论保证,但其仍然是一种快速稳定的神经网络训练算法.

设L表示训练的损失函数,其数学表达式为

(14)

模型的校准问题通常可转化为解决以下最小二乘问题,以找到网络中最优的参数θμ和θσ:

(15)

其中θμ=(Wμ,bμ),θσ=(Wσ,bσ).下面以Wμ中的第一个元素W1为例给出计算损失函数关于参数偏导数的过程:

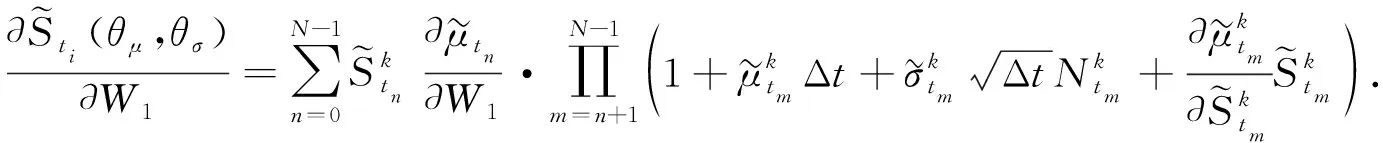
(16)

式(16)右端包含许多项的乘积,如果连乘项中某一项的值很小,则可能导致整体为零,称为梯度消失.由于式(16)中的连乘项内每项都包含一个常数1,因此乘积不可能接近于0,这种结构解决了梯度消失的问题,使训练更稳定.

算法1PyTorch神经网络NSDE模型.

输入: 价格数据矩阵x∈958×1,漂移网络Drift,扩散网络Diffusion,迭代次数为100;初始学习率α= 0.001;损失函数为

输出: 每次迭代的损失值,训练后漂移网络和扩散网络隐含层的权重和偏移参数Wμ*,bμ*,Wσ*,bσ*,训练后的股票价格数据(Si)i∈[1,958].

步骤1) 随机初始化漂移网络和扩散网络隐含层的参数:Wμ(0),bμ(0),Wσ(0),bσ(0).

步骤2) 构造一个NSDE类、前向传播:

将漂移网络Drift和扩散网络Diffusion添加到迭代更新计算股票价格的表达式中,

for迭代次数k=0 to 99 do

end for

步骤3) 计算损失:

for迭代次数k=0 to 99 do

end for

步骤4) 反向传播、更新漂移和扩散网络的参数:

for迭代次数k=0 to 99 do

loss.backward( )

end for

步骤5) 动态调整学习率:

for每次迭代epoch=1,2,…,99 do

end for.

设迭代次数为100次,迭代完成时损失函数收敛,即经过训练网络达到了损失很小的状态,使用NSDE模型模拟的股票价格准确率很高.整个实验是在PyTorch中完成的,算法流程如算法1,唯一调优的超参数是优化器中的初始学习率.为使实验能够加速收敛,选择动态变化的学习率,随着迭代次数的增加学习率越来越小.实验平台采用具有Geforce RTX GPU的Linux服务器,内存64 GB,编程语言为Python.

2.2 实证分析结果

为检验NSDE模型的性能进行一个数值实验,在测试集上分别使用NSDE模型和Black-Scholes(BS)模型模拟股票价格.NSDE模型用的回报率和波动率是在训练集上训练得到的,Black-Scholes模型中的回报率和波动率采用训练集数据的平均回报率和历史波动率.对比两个模型的预测精度时,采用MAE,MSE,RMSE(均方根误差)和R24个评价指标.

NSDE模型经过训练得到的回报率和波动率如图5所示.由图5可见,NSDE模型经过训练后的回报率和波动率随时间和股票价格时刻变动,并非像Black-Scholes模型的假设那样是常数.

图5 NSDE模型训练后的回报率(A)和波动率(B)Fig.5 Return rate (A) and volatility (B) of NSDE model after training

图6 测试集上NSDE模型与Black-Scholes模型预测结果对比Fig.6 Comparison of prediction results of NSDE model and Black-Scholes model on test set

测试集上NSDE模型与Black-Scholes模型预测结果对比如图6所示.由图6可见: 由Black-Scholes模型在未来200 d(测试集)预测的股票价格明显不接近真实值,但NSDE模型的预测效果很好;NSDE模型的预测误差曲线也整体位于Black-Scholes模型预测误差曲线的下方.为更具体地比较两个模型的差异,表1列出了NSDE模型和Black-Scholes模型的损失评价指标.表1中的结果证实了根据图像得出的结论是正确的,在测试集上本文提出的NSDE模型的MAE,MSE和RMSE均小于Black-Scholes模型对应的值,而R2高于Black-Scholes模型的计算值.说明NSDE模型预测的股票价格更接近真实股票价格,预测效果明显优于Black-Scholes模型.

表1 NSDE模型和Black-Scholes模型测试集股票价格预测结果对比

3 近似目标期权价格

无论是Black-Scholes模型还是NSDE模型,都依赖于股票的一些基本信息,如每个时刻股票的价格数据,当无法观测每个时刻的股票价格时,两个模型都会失效,其对应的期权价格也无法计算.下面考虑在未知收益率,仅已知波动率和初始时刻股票价格数据的情况下,对期权价格进行估计和预测.

Wasserstein距离目前在统计和机器学习中应用广泛[12].例如:lvarez-Esteban等[13]研究了一种基于截尾分布之间的L2-Wasserstein距离的分布相似性分析方法,通过实例验证了这种数据驱动的方法可使分布之间的相似性最大化;Arjovsky等[14]将GAN与Wasserstein距离结合,提出的WGAN能通过训练鉴别器达到最优性来连续估计EM(earth-morer)距离,解决了GAN存在的主要训练问题.本文利用Wasserstein距离可作为概率测度之间度量的性质,考虑将期权价格用风险中性等价测度表示,最后给出一个关于目标期权价格的约束.

3.1 目标期权价格表示

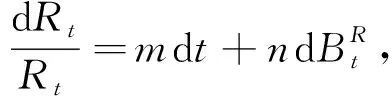
(17)

其中回报率m∈,波动率n>0.设目标期权0时刻的价格为Q0,可以用与 P对应的风险中性等价鞅测度 H表示为

Q0=EH[e-rTφ(RT)],

(18)

其中φ(RT)=(RT-K)+,两份期权具有相同的到期日T和行权价格K,φ(·)为正部函数.由引理2可得Q0在自然概率测度 P下的表达式为

(19)

由于回报率m是未知的,除R0外Rt是不可观测的,因此无法再使用NSDE模型训练回报率和波动率.下面考虑用已知的期权价格P0预测估计未知的期权价格Q0,考虑到P0和Q0都可以在风险中性等价鞅测度下计算,因此选择使用Wasserstein距离作为约束,给出期权价格的一个估计.

3.2 目标期权价格近似误差

下面给出用P0近似Q0的近似误差.

定理1目标期权的价格Q0可以用包含其标的资产且到期日和行权价格都相同的期权价格P0近似,近似误差为

erT|P0-Q0|≤W1(νQS,νHR),

(20)

证明: 首先注意到

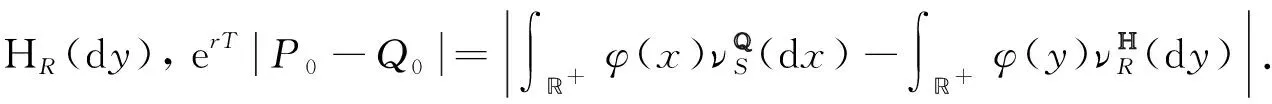
(21)

从而证明了不等式成立.由于在风险中性等价测度下,收益率等于无风险利率,所以对任意的x>0,有

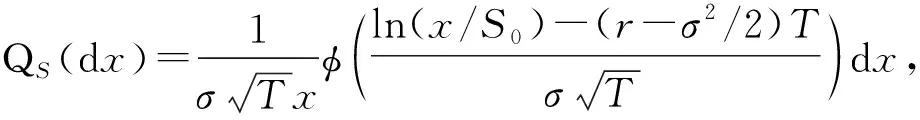
证毕.

其中:W1(νQS,νHR)表示νQS与νHR之间的Wasserstein-1距离;

下面给出简化后近似误差计算公式的结果.

推论1目标期权的价格Q0可以用P0近似,近似误差为

(23)

4 结果与讨论

基于现有的Black-Scholes模型进行期权定价,在实际应用中存在回报率和波动率难估计的问题.如果考虑简单地将深度学习理论应用于期权定价,则需要通过获取大型数据集为网络提供信息,从而带来较大的计算复杂度.本文考虑将经典Black-Scholes模型与深度学习相结合,将原来的回报率和波动率参数化为神经网络,建立NSDE模型.在实验中选取2012—2016年的股票价格数据用来训练和测试网络,实验结果表明,用NSDE模型训练可以得到动态变化的漂移项和扩散项,该模型预测效果优于Black-Scholes模型.当回报率未知且除初始时刻外每时刻股票价格不可观测时,NSDE模型不再能通过训练预测股票价格,因此本文在理论上提供了另一种估计方法,用一个已知期权的价格近似目标期权价格,并给出了近似误差的计算公式.

事实上,Black-Scholes模型在期权定价中出现的问题还有很多,例如,Black-Scholes模型假设波动率是常数,但实际市场中波动率常呈现“微笑”形状,因此对于NSDE模型可以添加针对波动率的约束进行优化.另一方面,在NSDE模型中采用随机梯度下降(SGD)法对网络权重进行更新,但SGD算法可能会导致收敛速度慢或陷入局部最小值等问题[15],而且如何选择合适的学习率作为初始值较困难.Shi[16]已经证明了学习率和动量系数这两个超参数在非凸优化问题中对线性收敛速度的重要作用,带动量的随机梯度下降可以加速收敛.因此,用带动量的随机梯度下降法替换SGD算法可以作为后续优化网络的主要工作.