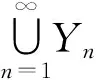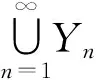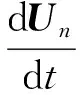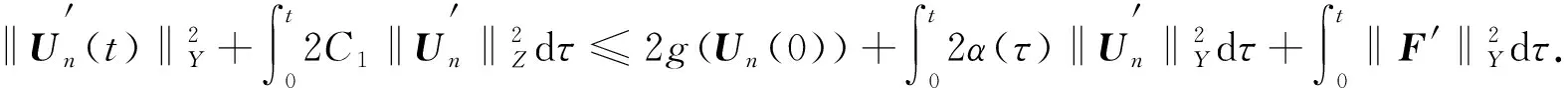二维不可压缩磁-微极流初边值问题的全局解
2023-11-24吴辰龙刘瑞宽
吴辰龙,刘瑞宽
(西南石油大学 理学院,成都 610500)
0 引 言
考虑如下二维不可压缩磁-微极流体动力学方程组:

(1)
其中:Ω⊂2为边界光滑的有界开区域;u(t,x)∈2,w(t,x)∈2,b(t,x)∈2和p(t,x)∈分别表示流速、微旋转速度、磁场强度和静水压力;f(t,x),g(t,x)∈2为已知的外力函数.本文考虑如下的齐次边界条件和初始条件:

(2)
u(0,x)=u0(x),w(0,x)=w0(x),b(0,x)=b0(x),x∈Ω,
(3)

磁-微极流方程常被用于描述具有微旋转效应的导电流体(如等离子体、液态金属)在磁场作用下的流动现象,对太阳或地球磁场的起源、超新星爆发、受控热核反应等研究具有重要意义,目前已得到广泛关注[1-8].例如,Rojas-Medar等[2-3]利用Galerkin方法讨论了方程组(1)在无滑移型边界条件下的全局弱解与局部强解,并解决了二维情形下弱解的唯一性问题;Ortega-Torres等[4]在小初值的前提下得到了全局强解的存在性;Yuan[5]获得了方程组(1)光滑解的一个爆破准则;Xu[6]通过Fourier局部化方法改进了三维磁-微极流问题一些已知的弱解正则性结果;Zhang等[7]在Tribel空间中建立了仅用速度场梯度控制的弱解的正则性准则.马天[9]建立了T-弱连续算子方法,该方法可有效解决一些非线性偏微分方程全局解的适定性问题;基于T-弱连续算子方法,马天等[10]讨论了一类二阶非线性抛物方程初边值问题全局强解的存在性与正则性;Zhang等[11]得到了一类描述多元体相分离现象的四阶拟线性演化方程的整体弱解的存在性结果;Wang等[12]获得了二维不可压缩Marangoni问题整体弱解的存在性与唯一性定理;Wu[13]证明了一类完全非线性发展方程强解的整体存在性.受上述研究启发,本文利用T-弱连续算子方法研究二维不可压缩磁-微极流初边值问题(1)-(3)全局解的存在性与唯一性.
1 预备知识
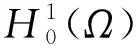

其中1≤p≤∞.
类似文献[14],定义如下函数空间:
并始终假设:

Y=U1×V1×W1,H=U2×V2×W2,Z=U3×V3×W3.
注意到L2(Ω,2)可进行形如L2(Ω,2)=U1⊕的Leray分解,这里

下面用P表示从L2(Ω,2)到U1的正交投影算子,即P是Leray投影算子.本文始终假设U=(u,w,b),F=(f,g,0),并定义算子G:H×(0,∞)→Y*为

(4)
这里Y*是Y的对偶空间.于是,初边值问题(1)-(3)可等价为如下形式:

(5)


成立,则U称为问题(5)的一个全局弱解.
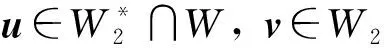
定义2[9]若对任意的xn∈W1,xn⇀x0,且有子列{xnk}∈W1满足






则在L2((0,T)×Ω)上对任意的|α|≤m-1,有Dαun→Dαu0.
2 主要引理与估计
下面总假设∂i=∂/∂xi,并约定出现指标i,j时,表示从1到2求和;出现指标k时,表示对1~3求和.为方便,记u=(u1,u2),w=(w1,w2),b=(b1,b2),u1,j=uj,u2,j=wj,u3,j=bj,j=1,2.
引理2若G为式(4)中定义的算子,则有如下不等式成立:
这里常数C>0.
证明: 对式(4)乘以U,并在Ω上积分可得
利用分部积分公式并结合divu=0,有
再注意到
则有
这里常数C>0.
引理3对任意的0 其中常数C>0. 证明: 定义算子 (6) 则对∀S∈Y,由分部积分公式有 注意到U∈L2((0,T),H)∩L∞((0,T),Y),S∈E,则 进一步,有 综合上述不等式,即有 引理4若G为式(4)中定义的算子,则G是T-弱连续的. 证明: 取L2((0,T),Z)中有界序列{Un}且Un⇀U0,则由引理1知,{Un}在L2((0,T),Y)中强收敛,即 Un→U0(L2((0,T),Y)), (7) 其中0 对∀S∈E,显然有 其中B为式(6)中定义的算子. 由分部积分公式,并结合式(7),(8)可得 同时有 从而 (13) 于是由式(9)~(13)可得 引理5若U=(u,w,b),S=(s1,s2,s3),则对任意的U∈H,S∈E, 成立,对任意的U,S∈E, 证明: 令U=(u,w,b),S=(s1,s2,s3),B为式(6)定义的算子,结合Hölder,ε-Young和Poincaré不等式及分部积分公式,可得 显然,泛函g:H→[0,∞)是有界的. 又对任意的U,S∈E,有 利用Hölder和ε-Young不等式,有 取X0=Y,X1/2=Z,则有如下插值不等式[15]: (15) (16) 这里X1/4=W1/2,2(Ω,2)×W1/2,2(Ω,2)×W1/2,2(Ω,2).利用分数阶Sobolev嵌入定理[15],有 (17) (18) 从而结合式(14)~(18),有 定理1令U0=U(0)=(u0,w0,b0),F=(f,g,0),且F(0,x)=0,则如下结论成立: 1) 对任意的U0∈Y,F∈L2((0,T),Y)和0 2) 对任意的U0∈H,F∈W1,2((0,T),Y)和0 记Yn=span{e1,…,en}.对方程(5)利用标准的Galerkin技术,并考虑如下常微分方程组: (19) (20) 在式(20)中令S=Un,则有 (21) 结合引理2与式(21),可得 利用Gronwall不等式,对任意的0 (23) 由式(22)显然可得 再结合式(23),可推出 (24) 从而由式(23)与式(24)可知 {Un}⊂L∞((0,T),Y)∩L2((0,T),Z), (25) 由引理3和式(19)可知 (26) (27) 由引理4知,算子G是T-弱连续的,因此对任意的S∈Yn,有 (28) 2) 由算子G的Fréchet可微性,并结合式(19),易见Un满足 (29) 由引理5可知 (30) 对任意的S∈Yn,有 (31) (32) 结合式(30)与式(32),有 (33) 由于E⊂H,U0∈H,因此在H中有Un(0)→U0.又由式(28)知α(τ)∈L1(0,T),则对式(33)应用Gronwall不等式,可得 利用中值公式,有 (34)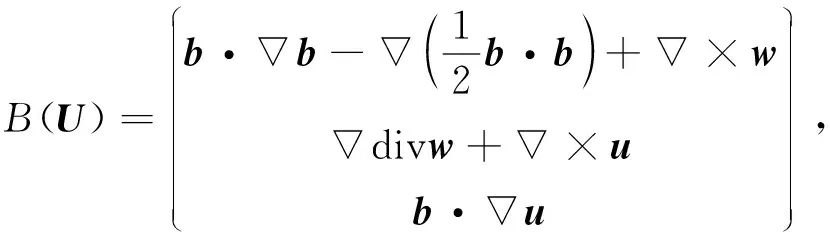

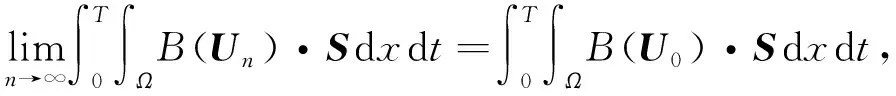





3 主要结果及其证明