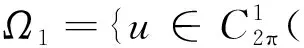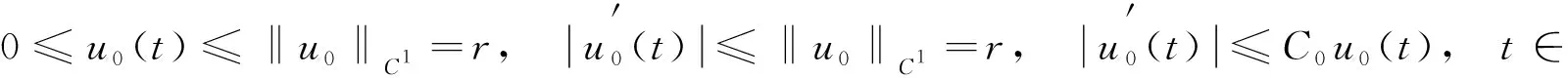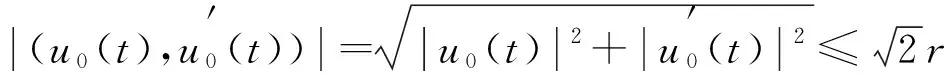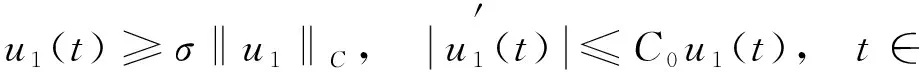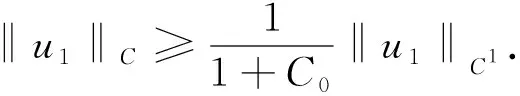具有非线性导数项的二阶常微分方程的正周期解
2023-11-24刘晓明李永祥
刘晓明,李永祥
(西北师范大学 数学与统计学院,兰州 730070)
-u″(t)+a(t)u(t)=f(t,u(t),u′(t)), t∈
正2π-周期解的存在性,其中: a: →(0,+∞)连续,以2π为周期;f: ×[0,+∞)×→[0,+∞)连续,f(t,x,y)关于t以2π为周期.在非线性项f(t,x,y)满足适当的不等式条件下,得到了该方程正2π-周期解的存在性.
0 引 言
目前,关于二阶常微分方程周期解的存在性研究已有很多结果,但已有工作主要集中在非线性项中不含未知函数导数的方程上,而对含未知函数导数的一般情形研究较少[1-5].本文研究非线性项中含未知函数导数的变系数二阶常微分方程
-u″(t)+a(t)u(t)=f(t,u(t),u′(t)),t∈
(1)
正2π-周期解的存在性问题,其中系数函数a与非线性项f分别满足下列条件:
(H1)a:→(0,+∞)连续,以2π为周期;
(H2)f:×[0,+∞)×→[0,+∞)连续,f(t,x,y) 关于t以2π为周期.
文献[6-10]研究了该问题的一些特殊情形.文献[6]讨论了a(t)恒为常数M及f不含导数项u′(t)的情形:
-u″(t)+Mu(t)=f(t,u(t)),
(2)
在f(t,x)关于x超线性或次线性增长的条件下,用锥映射的Krasnoselskii不动点定理,获得了方程(2)正2π-周期解的存在性.文献[7]用正算子扰动方法与锥映射的Krasnoselskii不动点定理获得了变系数二阶微分方程
-u″(t)+a(t)u(t)=f(t,u(t))
(3)
正周期解的存在性与多重性结果.文献[8]和文献[9]用锥上的不动点指数理论分别对方程(2)和(3)建立了正周期解存在的特征值准则,即当f(t,x)连续,满足下列条件之一时方程有正周期解:
(i)f0<λ1,f∞>λ1;
(ii)f0>λ1,f∞<λ1.
其中

(4)
而λ1为相应的线性周期特征值问题的最小正实特征值.对方程(2),λ1=M.文献[8]和文献[9]的特征值准则分别包含并改进了文献[6]和文献[7]的结果.此外,文献[11-14]讨论了二阶微分方程
u″(t)+a(t)u(t)=f(t,u(t))
(5)
正周期解的存在性.与方程(3)不同,讨论方程(5)的正周期解要求系数函数a(t)的值适当小,如文献[13]要求:a(t)≤1/4,t∈[0,2π].此时,方程(5)的周期问题对应的Green函数是非负的,其正周期解可化为锥映射的不动点,从而可用与文献[6-9]类似的方法获得方程(5)的正周期解.

1 预备知识
设C2π()是以2π为周期的全体连续函数按最大模范数构成的Banach空间.一般地,对n∈,()表示以2π为周期的全体n阶连续可微函数按范数
为讨论非线性方程(1)正2π-周期解的存在性,先考虑相应的线性方程
-u″(t)+a(t)u(t)=h(t),t∈
(6)
2π-周期解的存在唯一性,其中h∈C2π().下面总假设a(t)满足(H1).令

(7)
则0 -u″(t)+Mu(t)=h(t),t∈. (8) 由文献[9]中引理2.1知,对∀h∈C2π(),方程(8)存在唯一2π-周期解 (9) 其中 (10) 由式(9)直接验证易知,方程(8)的周期解算子T:C2π()()是线性有界算子.记 取正常数 (11) 引理1线性方程(8)的周期解算子T作为C2π()到C2π()的线性有界算子,其范数且当()时,线性方程(8)的2π-周期解u=Th满足估计: u(t)≥σ0‖u‖C, |u′(t)|≤C0|u(t)|,t∈. (12) 证明: 对∀h∈C2π(),由式(9)及式(10),有 (13) 即式(12)的第一个估计式成立.另一方面,由式(9)得 从而由式(13)可得 即式(12)的第二个估计式成立.证毕. 下面考虑变系数线性二阶微分方程(6)的2π-周期解的存在性. 引理2对∀h∈C2π(),线性方程(6)存在唯一的2π-周期解(),且周期解算子S:C2π()()是线性有界算子.当()时,线性方程(6)的2π-周期解u=Sh是非负的,且满足式(12). 证明: 改写方程(6)为如下形式: -u″(t)+Mu(t)=Bu(t)+h(t),t∈, (14) 其中B:C2π()→C2π()为乘积算子 Bu(t)=(M-a(t))u(t),t∈. (15) 易见,B:C2π()→C2π()为正的线性有界算子,其范数‖B‖=M-m.按算子T:C2π()→C2π()的定义,方程(14)的2π-周期解等价于Banach空间C2π()中的算子方程 (I-TB)u=Th (16) 的解,其中I是C2π()中的单位算子.因为故由单位算子扰动定理,I-TB在C2π()中有有界逆算子,且其逆可展开为幂级数: (17) 故方程(16)(等价地方程(6))有唯一的2π-周期解 u=(I-TB)-1Th=∶Sh. (18) 由式(17),S=(I-TB)-1T可展开为 (19) 其中, (20) 为C2π()中的正线性有界算子.由T:C2π()()的有界性,S=TQ为C2π()到()中线性有界算子. u=Sh=T(Qh)=Th1, (21) 其中h1=Qh.由式(20),Q:C2π()→C2π()为正线性算子,故().因此,由引理1知,u=Th1满足估计式(12). 下面考虑方程(6)相应的周期线性特征值问题: -u″(t)+a(t)u(t)=λu(t),t∈,(). (22) (23) 证明: 定义微分算子L:D(L)⊂C2π()→C2π()为 (24) 则特征值问题(22)可化为算子L的特征值问题 Lu=λu,u∈D(L). (25) 由引理2,L有有界逆算子L-1=S.因为S:C2π()()有界,故由嵌入()C2π()的紧性及引理2知,S:C2π()→C2π()是正的线性全连续算子.取h0(t)恒为1,则由引理2知,u=Sh0满足估计式(12),从而有 Sh0≥‖Sh0‖Ch0. (26) 将式(26)两端用S累次作用,并由S的正性可得 Snh0≥‖Sh0‖Cnh0,n=1,2,…, 因此有 由Gelfand谱半径公式知,S的谱半径为 (27) 由式(19)及式(9),有 因此λ1≥m,于是λ1∈[m,M]. (28) F(u)(t)∶=f(t,u(t),u′(t)),t∈, (29) Au∶=S(F(u)),u∈K. (30) 由S:C2π()()的有界性及嵌入()()的紧性知,S:C2π()()全连续.因此,由式(30)定义的A:K→K全连续.再由算子S的定义,方程(1)的正2π-周期解等价于A的非零不动点.下面用锥上的不动点指数理论[16]寻找A的非零不动点. 下面讨论非线性方程(1)正2π-周期解的存在性.设σ0和C0是式(11)定义的正常数,λ1是线性特征值问题(22)的最小正实特征值. 定理1假设条件(H1),(H2)成立.若f:×[0,+∞)×→[0,+∞)还满足下列条件: 1) 存在常数a,b≥0满足a+C0b<λ1及常数δ>0,使得 f(t,x,y)≤ax+b|y|,x≥0,y∈, |(x,y)|≤δ; 2) 存在常数c>λ1及常数H>0,使得 f(t,x,y)≥cx,x≥0,y∈, |(x,y)|≥H. 则方程(1)至少有一个正2π-周期解. (31) μAu≠u,μ∈(0,1],u∈K∩∂Ω1. (32) (33) 因为u0∈K∩∂Ω1,由K和Ω1的定义,有 (34) 将方程(33)两端同乘φ1(t),然后从0到2π积分,并应用不等式(34),得 对式(35)左端应用分部积分和式(23),有 从而由式(35),得 (36) 因为u0∈K,φ1=S(λ1φ1)∈K,由锥K的定义,有u0(t)≥σ0‖u0‖C,φ1(t)≥σ0‖φ1‖C,t∈.故有 于是由式(36)得λ1≤a+C0b,与条件1)中的假设矛盾.因此式(32)成立.从而由不动点指数理论的同伦不变性,有 i(A,K∩Ω1,K)=1. (37) 其次,令R>(1+C0)H/σ0.因为φ1=S(λ1φ1)∈K,故φ1∈K{θ}.下证A在K∩∂Ω2上对e=φ1满足缺方向性条件: u-Au≠τφ1,τ≥0,u∈K∩∂Ω2. (38) 反设式(38)不成立,则存在τ1≥0及u1∈K∩∂Ω2,使得u1-Au1=τ1φ1.因为 u1=Au1+τ1φ1=S(F(u1))+τ1S(λ1φ1)=S(F(u1)+τ1λ1φ1), (39) 又因为u1∈K∩∂Ω2,由K和Ω2的定义,有 (40) (41) 于是,由式(40)的第一个不等式,有 (42) 将方程(39)两端同乘φ1(t),再从0到2π积分,并对其左端应用分部积分,右端应用不等式(42),有 i(A,K∩Ω2,K)=0. (44) 从而由式(37)和式(44)及不动点指数的区域可加性,有 定理2假设条件(H1),(H2)成立.若f:×[0,+∞)×→[0,+∞)还满足下列条件: 1) 存在常数c>λ1及δ>0,使得 f(t,x,y)≥cx,x≥0,y∈, |(x,y)|≤δ; 2) 存在常数a,b≥0满足a+C0b<λ1及常数H>0,使得 f(t,x,y)≤ax+b|y|,x≥0,y∈, |(x,y)|≥H. 则方程(1)至少有一个正2π-周期解. i(A,K∩Ω1,K)=0. (45) 类似于式(37)的证明,当R适当大时,应用条件2)可证得 i(A,K∩Ω2,K)=1. (46) 于是由式(45),(46),有 注1在定理1中,条件1)与2)分别允许当|(x,y)|→0和|(x,y)|→∞时,非线性项f(t,x,y)关于x和y超线性增长,典型的例子是关于x和y的幂函数: (47) 其中α,β>0是常数.显然,fα,β(t,x,y)满足条件(H1).易验证,当α,β>1时,f1(t,x,y)满足定理1中条件1)知2).因此,条件1)和2)允许非线性项f(t,x,y)关于x和y任意阶超线性增长. 注2在定理2中,条件1)和2)分别允许当|(x,y)|→0和|(x,y)|→∞时,非线性项f(t,x,y)关于x和y次线性增长,例如,当α,β∈(0,1)时,式(47)定义的幂函数fα,β(t,x,y),此时易验证fα,β(t,x,y)满足定理2中条件1)和2). 注3在定理1和定理2中,当f(t,x,y)不显含y,退化为f(t,x)时,由式(4)易验证: 定理1中条件1) ⟺f0<λ1, 定理1中条件2) ⟺f∞>λ1; 定理2中条件1) ⟺f0>λ1, 定理2中条件2) ⟺f∞<λ1. 因此,定理1的条件退化为(i),定理2的条件退化为(ii).此时定理1和定理2恰为文献[9]中的特征值准则.故本文定理1和定理2概括并推广了文献[6-9]中的主要结果. 此外,本文定理1的不等式条件允许非线性项f(t,x,y)关于x和y任意阶超线性增长,而已有的涉及超线性增长的工作,如关于周期问题的工作[3-4]和两点边值问题的工作[17-18],均要求f(t,x,y)关于y的增长满足Nagumo条件.Nagumo条件限制了f(t,x,y)关于y至多二次增长,本文定理1突破了该限制.
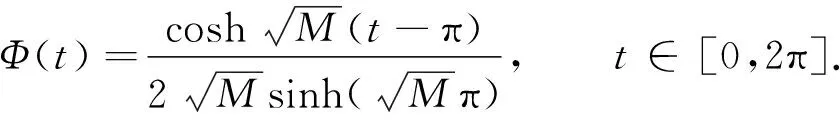
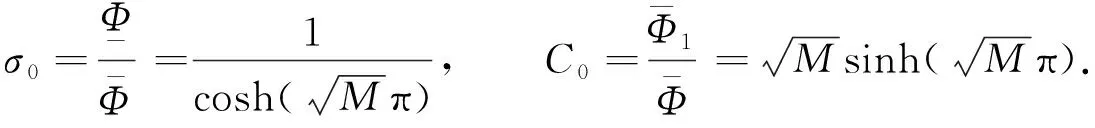
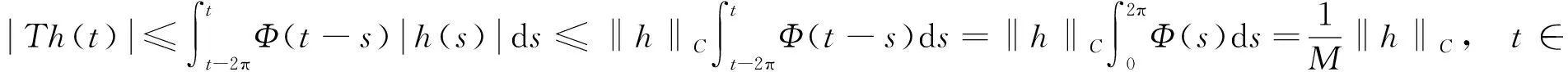

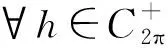






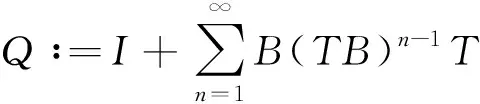


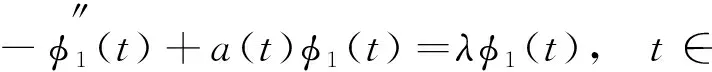






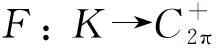
2 主要结果