单而芳, 吕文蓉, 史纪磊,2

(1.上海大学 管理学院,上海 200444; 2.江苏海洋大学 商学院,江苏 连云港 222005)

0 引言

可转移效用合作对策[1],简称TU-对策,是描述参与者通过组建合作联盟产生合作利益的基本模型。该模型假定任何有限参与者间都能够合作,形成可行联盟,产生合作效用。在这一基本假设下,为合理分配参与者合作产生的效用,Shapley值[2]、Banzhaf值[3]等经典的合作对策分配规则应运而生,并已广泛应用于经济、社会、政治及军事等各个领域。例如,Banzhaf值可用于个人社会排名方案的设计[4]、太阳能光伏发电系统的可靠性评估[5]、家庭电网的可靠性分析[6]及风险分摊[7]等问题中。

然而,在现实中,参与者间的合作往往受各种合作结构的制约,导致一些联盟并不能真正形成。考虑合作结构对参与者合作产生的影响,MYERSON[8]提出了具有图结构的TU-对策,又称通讯情形对策,简称图对策。图对策以图描述参与者间的合作结构,图的点表示参与者,图的边表示参与者间存在某种双边联系。图对策假定只有连通的联盟才能完全合作,产生合作效用,而其它联盟的效用只能由它包含的连通分支的效用之和得到。进一步,MYERSON定义了图限制对策下的Shapley值,并将该值作为图对策下的分配规则,命名为Myerson值。事实上,Myerson值是Shapley值在图对策上的推广。关于Shapley值的其他拓展研究可参见单而芳等[9,10]、李理和单而芳[11]的研究。而在Myerson值的思想基础上,ALONSO-MEIJIDE和FIESTRAS-JANEIRO[12]将Banzhaf值推广到了图对策中,定义了图限制对策下的Banzhaf值,给出了图对策下一个新的分配规则,即Banzhaf图值。Banzhaf图值可由公平性、隔离性、合并性、分支总贡献性和平衡贡献性给出四种公理化刻画。

图对策虽用图反映了参与者间存在的某些双边联系,但并非所有参与者间的联系都是双向的。例如,自然界中水资源循环(降雨、蒸发、下渗、径流等)的每个环节均有明确的方向性;南水北调工程从长江调水,修建渠道,依次流经北方地区,同样具有方向性[13];工业用水系统将工业用水首先用于生产用水子系统,之后将生产用水子系统产生的污水排放到污水处理子系统中,此过程也具有严格的方向性[14];而根据河流的流向,公共河流的用水主体具有上、下游关系,因此在研究公共河流的资源分配问题时,也不可不考虑其模型的方向性[15]。为描述此类合作对策,学者们将有向图引入了合作对策中,开始研究具有有向图结构的TU-对策,简称有向图对策。在有向图对策的研究中,学者们给出了可行联盟的多种定义,如KHMELNITSKAYA等[16]定义分层联盟为有向图对策中的可行联盟;LI和SHAN[17]则定义了强分支作为有向图对策中的可行联盟,假定强连通的联盟才能获得完全的效用,而非强连通联盟的效用由其所包含的所有强分支效用之和实现。LI和SHAN[17]的研究使寻找有向图对策中的可行联盟变得极为简便,也为进一步研究有向图对策中的分配规则提供了便利。

本文旨在将Banzhaf值推广到有向图对策中,提出并刻画有向图对策下的一个新分配规则,即有向Banzhaf值。我们定义了强分支点和必要边两个概念,并引入了三个性质:准隔离性、收缩性和强分支总贡献性。在此基础上,给出了有向Banzhaf值的两个公理化刻画。最后,以湿地水循环为例对该值展开了应用分析。

下一节给出本文需要的基本概念和记号。第二节定义强分支点等概念,并给出有向Banzhaf值的计算公式。第三节引入相关性质,对有向Banzhaf值进行公理化刻画。第四节以湿地水循环系统为例,分析有向Banzhaf值的特点。最后,总结了本文所做工作并给出注记。

1 预备知识

1.1 TU-对策

可转移效用合作对策[1],简称TU-对策,由二元组(N,v)组成,其中N={1,2,…,n}是有限参与者集,v是定义在2N={S|S⊆N}上的特征函数,且规定v(Ø)=0。对任意非空联盟S⊆N,v(S)表示联盟S的效用,|S|或s表示联盟S的基数。记所有TU-对策的集合为GN。为方便起见,我们将v({i,j,…,k}),S∪{i}和N{j}分别简记为v(i,j,…,k),S∪i和Ni。

对于TU-对策(N,v),支付向量x=(x1,x2,…,xn)∈Rn是一个n-维向量,其中xi是指给参与者i∈N的支付。TU-对策的一个(单值)分配规则或者值是一个函数f:GN→Rn,也即f指派给每个(N,v)的一个支付向量f(N,v)∈Rn。对于TU-对策和任意的参与者i∈N,著名的分配规则Banzhaf值β(N,v)定义为[3]:

(1)

1.2 图和图对策

图由(N,L)表示,其中N={1,2,…,n}称为图的节点集,而L⊆LN={{i,j}|i,j∈N,i≠j}称为图的(无向)边集。LN是N上的完全图。记所有图(N,L)的集合为LN。为简便起见,我们将边{i,j}简记为ij,而图(N,L)简记为L。

对任意S⊆N,联盟S的导出子图表示为(S,L|S),其中L|S={ij∈L|i,j∈S}。如果ij∈L,则称节点i与j是直接相连的。如果对任意的k=1,2,…,t-1,都有ikik+1∈L,则称互异点列(i1,i2,…,it)是(N,L)中的一条路。如果节点i和j之间存在一条路,则称节点i和j是连通的。如果S中任意两点都是连通的,则联盟S是连通的。在子图L|S中,S的每个极大连通子集称为它的一个分支。记S的所有分支的集合为S/L。特别地,把的所有分支的集合记为N/L。

以图作为合作结构,MYERSON[8]引入了具有图结构的TU-对策,又称通讯情形对策,简称图对策。图对策由三元组(N,v,L)组成,其中(N,v)表示TU-对策,(N,L)表示图。对任意(N,v,L),i∈N,Banzhaf图值ξ(N,v,L)[12]定义为:

ξi(N,v,L)=βi(N,vL),

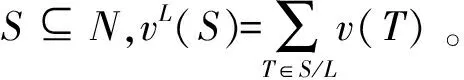
2 有向图对策下的Banzhaf值

2.1 有向图

有向图由(N,D)表示,其中N表示节点集,而D是由N的有序对(i,j)组成的有向边集。(i,j)∈D表示由i到j的一条弧。记所有有向图集合为DN。

对任意S⊆N,(S,D|S)表示联盟S在D上的导出子有向图,其中D|S={(i,j)∈D|i,j∈S}。如果对于任意的t=1,2,…,k,都有i0=i,ik=j且(it-1,it)∈D|S,则称互异点列P=(i0,i1,…,ik)⊆S(k≥1)是由到的一条有向路。若在D|S中同时存在i到j及j到i的有向路,则称节点i,j∈S是强连通的。如果联盟S中任意两点都是强连通的,则称联盟S是强连通的。在(S,D|S)中,S的每个极大强连通子集称为S的一个强分支。记S的所有强分支的集合为S/D。特别地,N/D表示N的所有强分支的集合。对每个有向图D而言,如果我们忽略它的每条有向边的方向,那么这个有向图对应着一个无向图。一般地,有向图D的强分支与这个无向图的分支(称为N的弱分支)是不同的。注意到强分支之间可以存在有向边相连,但分支之间是不存在任何边的。

有向图中的孤立点是指不与任何有向边关联的点。在强连通的定义下,将独自形成一个强分支的节点定义为强分支点。注意,强分支点允许关联单方向的有向边。对任意(i,j)∈D,D(i,j)表示D去掉有向边(i,j)后形成的有向图。对任意的强分支S∈N/D(S≥2)和(i,j)∈D|S,如果|S/(D|S(i,j))|>1,则称有向边(i,j)是必要的。我们记所有与i关联的有向边集合为Di={l∈D|i∈l},则D-i=DDi表示去掉所有与关联的有向边后形成的子有向图。

如图1所示,图中的节点集为N={1,2,3,4,5,6},有向边集为D={(1,2),(2,3),(3,4),(4,1),(3,1),(4,5)}。根据强分支的定义,可知N/D={{1,2,3,4},{5},{6}}。在强分支S={1,2,3,4}中,删掉有向边不会影响强分支的强连通性,因此有向边是非必要边。除此之外,S中的其他有向边均为必要边。参与者5为强分支点,但非孤立点。参与者6既是强分支点也是孤立点。

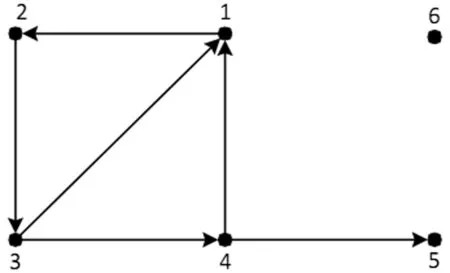
图1 6个参与者组成的有向图

2.2 有向Banzhaf值

(2)

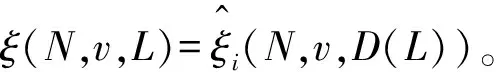
3 有向Banzhaf值的公理化刻画

为给出有向Banzhaf值的公理化刻画,首先给出它所满足的一些性质公理。

fi(N,v,D)-fi(N,v,D{(i,j)})

=fj(N,v,D)-fj(N,v,D{(i,j)}),

则称f具有公平性。

公平性是指当参与者i到j之间的有向边被断开后,对两个参与者支付产生相同的影响。

准隔离性是指与任意联盟均无法产生合作效用的参与者,即强分支点,只能获得其自身产生的收益。

Nij=N{i,j}∪{p}

(3)

对任意的l,k∈Nij,(l,k)∈Dij当且仅当满足如下条件

(4)

特征函数vij定义为

(5)

收缩性是指:收缩有向图中的一条必要边时,参与者间的合作结构不会受到影响,进而不会影响参与者的支付。

在值的公理化过程中,若使用到的公理化性质大于等于三个,则需要说明性质间的无冗余性。下面,我们将举例说明定理1中所使用的性质是无冗余的。

1)有向Myerson值,即μ(N,v,D)=Sh(N,vD)满足准隔离性和公平性,但不满足收缩性。

其中i∈Ci∈N/D。可验证该值满足收缩性和准隔离性,但不满足公平性。

接下来,我们将引入另外两个新性质,给出有向Banzhaf值的第二种公理化刻画。

则称f具有强分支总贡献性。

4 湿地水循环系统分析

湿地被誉为“地球之肾”,是“淡水之源”和最大的“淡水贮存库”。我国湿地维持着约2.7 万亿吨淡水,占全国可利用淡水资源总量的96%。此外,湿地还是高效的“淡水净化器”,能够很好的去除城镇污水处理厂尾水中的污染物,起到进一步净化的作用[18]。保护湿地、实现湿地资源可持续利用,是维护水资源安全的根本之策。湿地水循环系统通过抽取湿地中的水资源用于农田灌溉、工业用水、城市用水、水产养殖等多方面,并将各个过程中产生的废水简单处理后排入湿地,利用湿地的净化功能进行再净化,以此形成对湿地水资源的循环利用。

现考虑由湿地1、泵站2、城市绿化3、工业生产4和污水处理厂5构成的简易湿地水循环系统,如图2。泵站2从湿地1中提取水资源,供给城市绿化3和工业生产4使用。之后,城市绿化3和工业生产4产生的污水经由污水处理厂5简单处理后重新排到湿地1中。在该系统中,湿地1的水资源用于城市绿化3或工业生产4时便可产生效用。因湿地1中的水资源必须由泵站2提取,所以只有包含{湿地1, 泵站2, 城市绿化3} 或{湿地1, 泵站2, 工业生产4}的集合才能够产生效用。湿地1的水资源循环利用率越高,产生的效用越大。为方便计算分析,假设湿地1的水资源经泵站2提取后,若只用于城市绿化3或工业生产4可产生40的效用,污水处理厂5加入时可提高循环利用率,产生100的效用;若同时用于城市绿化3和工业生产4,可产生60的效用,污水处理厂5加入时,产生140的效用。

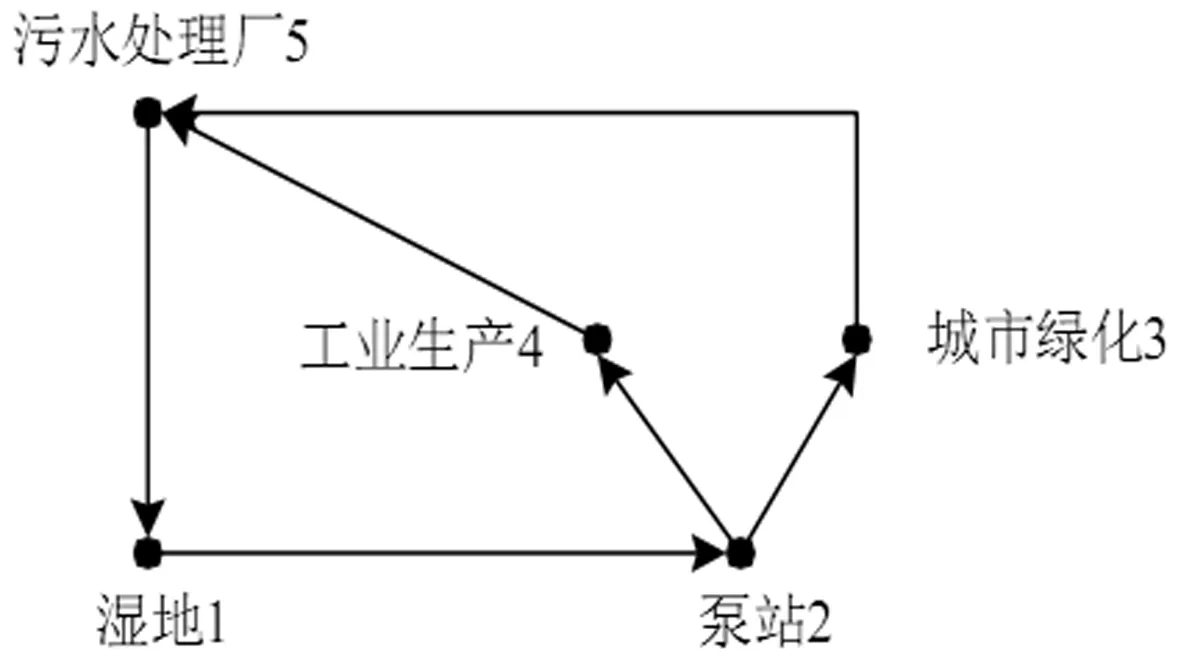
图2 湿地水循环系统结构图

现将该系统抽象为有向图对策进行分析。系统中各环节可视为参与者,即N={1,2,3,4,5}。湿地水资源的流动方向可视为有向边,即D={(1,2),(2,3),(2,4),(3,5),(4,5),(5,1)}。根据湿地水资源的效用情况,特征函数可定义为:

表1 湿地水循环系统中各值计算结果

表1数据表明,Banzhaf值和Banzhaf图值对五个功能点的效用评估结果均为:湿地1=泵站2>城市绿化3=工业生产4=污水处理厂5;而有向Banzhaf值的效用评估结果为:湿地1=泵站2=污水处理厂5>城市绿化3=工业生产4。对比分析可知,有向Banzhaf值具有以下特点:

1)结构上与湿地水循环系统更为契合。Banzhaf值未考虑功能点间水资源的流动限制;Banzhaf图值虽引入图结构描述水资源的流动限制,却未考虑水资源的流向;而有向Banzhaf值引入有向图结构,更好地契合了湿地水循环系统的结构。

2)突出了污水处理厂5的地位,评估结果更为合理。三个值虽均能够体现湿地1不可或缺的“源头”作用和泵站2 至关重要的“枢纽”作用。而在该系统中,污水处理厂5作为湿地水循环系统中必不可少的一环,仅在有向Banzhaf值下评估到了较高的结果。Banzhaf值和Banzhaf图值的结果却表明,污水处理厂5和具有可替代性的用水单位效用相同。显然,有向Banzhaf值更具合理性。

3)利于维持湿地水循环系统的稳定性。Banzhaf值和Banzhaf图值对各功能点的评估结果极差较大,易引发“公平性”问题。有向Banzhaf值的评估结果既能体现功能点的价值,也不会产生过大极差,利于维持系统稳定。

最后,我们从公理化性质角度进一步验证有向Banzhaf值的优势。

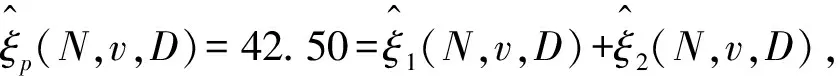
2)公平性。以有向边(2,3)为例,去掉该有向边后重新计算泵站2和城市绿化3的有向Banzhaf值,分别为12.50和0,显然满足公平性。这些性质也从不同角度反映了有向Banzhaf值评估结果的合理性。

5 结论及注记

本文使用强分支作为有向图对策中的可行联盟,提出了有向图对策下的一类新分配方案——有向Banzhaf值。证明了该方案可由准隔离性、收缩性、公平性和强分支总贡献性给出两种公理化刻画,这些公理化性质从不同角度说明了该方案的公平合理性。实际上,利用公平性和平衡贡献性以及双边公平性[17]间的关系,还可以进一步给出其他形式的刻画。此外,通过湿地水循环系统的例子,说明了有向Banzhaf值的应用场景。在这个例子中,由于水流具有明确的方向性,且循环系统是一个闭环结构,因此需要考虑闭环有向图结构对其产生的影响。而现实中其他有向循环系统(如闭环供应链、农业生态循环等)也可用有向Banzhaf值评估各环节的效率,这为各功能点合理配置资源、提升循环系统整体效用提供了理论依据。