马国耀,蒋 奇†,宗西举

(1.山东大学控制科学与工程学院,山东济南 250061;2.济南大学信息科学与工程学院,山东济南 250022)

1 引言

大约1750年,Euler-Bernoulli梁方程被提出.随着外层空间技术的不断发展,人们愈发认识到Euler-Bernoulli梁方程作为一个基准系统对推动科技发展的重要性.伴随着理论研究发展的日趋成熟,许多有效方法被应用于实现Euler-Bernoulli梁方程系统的稳定性,如Backstepping变换法[1-2]、Lyapunov能量方法[3]和频域方法[4]等.但是,这些手段在求证偏微分系统稳定上仍然存在计算困难等问题.伴随着Riesz基性质和偏微分系统稳定关系的确立,基于Riesz基求证偏微分系统稳定性已成为一种趋势.在这个理论中,通过求解谱增长条件,明确在该系统条件下Riesz基性质,即可实现偏微分方程系统的稳定性证明[5-7].但是,当系统外部存在扰动或出现内部不确定性时,文献[5-7]将难以实现稳定.

为解决该问题,许多经典算法被应用到Euler-Bernoulli梁方程上,如未知参数的自适应控制[8-9]、滑模控制[10-12]等方法.上述方法大都是以控制器的鲁棒性对干扰进行抵抗,或者说是基于一种最坏情况下的反馈控制.这类控制器通常过于保守且容易出现“抖振”问题.

韩京清老师在1998年首次提出了自抗扰控制(active disturbance rejection control,ADRC)的概念[13].ADRC的突出优点是设计了一个扩张状态观测器(extended state observer,ESO)来估计扰动,进而使用其估计值补偿系统回路中的各种不确定因素.随着研究的不断深入,将ADRC 引入到偏微分方程(partial diffrential equation,PDE)的理论正在逐步完善.文献[14]针对带有边界扰动的Kirchhoff板,设计了一类状态观测器.该状态观测器由无限多个常微分方程构成,借助ADRC技术,抵消了来自多维Kirchhoff板的时间和空间变化的边界扰动,但随着时间可变增益的不断增加,其对高频噪声的鲁棒性也会逐渐变差.文献[15]针对热方程系统的扰动抑制,构建了两个辅助系统.一个用于分离扰动和控制,另一个用来估计扰动,在ESO的帮助下,构建了控制器,进而消除了反馈回路中存在的干扰.文献[16]借助文献[15]的研究思路,基于波动方程,实现了扰动的估计和控制器的设计.但是,无论是热方程还是波动方程,其阶数和处理难度都弱于Euler-Bernoulli梁.随着理论研究的不断深入,在文献[17-20]中,作者将上述状态观测器的设计思想应用到了带有不确定性因素和外界扰动的Euler-Bernoulli梁方程系统上.文献[21]针对Euler-Bernoulli梁方程系统,设计了一个无限维估计器来估计扰动,并基于速度反馈和角速度反馈设计了两种不同的控制器,最后利用Riesz基方法证明了闭环系统的指数稳定性.2017年,文献[22]整理了ADRC的一些新老结论,系统阐述了ADRC在偏微分方程上的应用,并以Euler-Bernoulli梁方程系统为例,详细解释了应用过程中的注意事项和方法.文献[23]在上述研究的基础上,将带有不确定性因素和外部干扰的Euler-Bernoulli梁方程系统应用至多智能体系统,并证明了其收敛性.但是,在文献[17]和文献[19-21]中,其Euler-Bernoulli梁方程系统的4个边界条件中有3个为0,这种边界条件实际上简化了状态观测器和边界控制器的设计.在文献[18]和文献[23]中,其不确定性施加在边界弯矩(关于x的二阶偏导)项上,在处理上相比于边界剪切力(关于x的三阶偏导)更为直观和容易.

本文针对带有边界扰动、内部不确定性和外部扰动的Euler-Bernoulli梁方程系统,提出一种基于干扰观测器的边界输出反馈控制.相比已有的研究成果,本文的创新点是: 1)系统边界条件不同.本文所考虑的Euler-Bernoulli梁方程系统其边界弯矩受边界角速度影响,并且边界剪切力受控制器和扰动的影响;2)针对具有该边界条件的系统,使用扰动观测器观测到内部不确定性和外部扰动二者的总扰动值,并且使用Riesz基方法,证明了与干扰观测器相关系统的稳定性;3)利用估计值,在系统的边界剪切力处设置边界输出反馈控制器,从而实现了系统的指数稳定.

本文的其余部分组织如下: 第2节,给出本文研究系统的方程,同时作出一些定义和合理假设.第3节,给出参考系统和干扰观测器的形式,同时证明相关系统的稳定性.第4节,借助文献[5]的部分结论,给出边界输出反馈控制器的形式,说明该反馈控制器和干扰观测器能够相互结合并稳定的原因.第5节,介绍一些数值模拟,验证所提出观测器和控制器的有效性.第6节,对本文进行总结.

2 系统描述

在本文中,考虑以下带有不确定影响的Euler-Bernoulli梁方程:

在系统(1)中,ω(x,t)表示梁在时间t和位置x的位移,(ω0(x),ω1(x))表示系统初始状态,ωt(x,t)和ωx(x,t)分别表示ω(x,t)关于变量t和变量x的导数,d ∈L∞(0,∞)表示未知的外部干扰,f(ω(·,t),ωt(·,t)):(0,1)×L2(0,1)→R表示系统内部的非线性映射,反映了系统的不确定性,ym表示可测量的输出信号,u0(t)表示设计的边界控制输入.

假设1对于不确定扰动f(·)和外部干扰d(t),假设存在∈R+和∈R+使

定义1为方便下文讨论,使用如下定义:

作为总干扰.

在系统(1)中,梁的一端是自由的,在另一端受梁的边界角速度、控制输入和未知扰动影响,本质上是受边界角速度影响的单铰链柔性机器人的振动控制.本文的目的是基于测量值ym,设计一个总扰动观测器和反馈控制器,利用扰动观测器和控制器产生的信号,使系统的状态ω(x,t)以指数形式收敛到零.

3 扰动观测器设计

在本节中,将利用系统输出ym设计一个不使用高增益的总干扰估计器.受文献[17][22]-[23]的启发,首先引入参考系统(5),即

其中k1是和系统(1)相同的可调节系数.显然,该系统完全取决于原系统(1)的输入和输出,故系统(5)为一个完全已知的系统.根据文献[24],当系统的控制输入u0(t)≡0时,系统(5)将以指数形式收敛到零.

系统(7)和系统(5)类似,由文献[24]可 知,当F(t)≡0时系统(7)将指数收敛.另外,系统(7)具有一个突出的优点,即其不受控制器u0(t)的影响,这就实现了控制与扰动的分离.由上述分析可知,可以根据系统(7)进行系统(1)总扰动的估计.

取系统(7)的状态空间为H=(0,1)×L2(0,1),其中,(0,1)表示Sobolev空间下满足边界条件的函数f ∈L2(0,1)具有平方可积的一阶和二阶弱导数.对∀(fi,gi)T∈H(i=1,2)定义其内积诱导范数为

进而系统(7)在状态空间H中可被重写为

算子A的情况如下:

其中δ为狄拉克分布.

从系统(7)中不难发现,算子A可生成一个C0-半群,算子B关于算子A生成的C0-半群是容许的[22].由于系统(7)的线性部分是指数稳定的,并且与控制无关,所以系统(7)的扰动观测器的设计要比原始系统(1)容易得多.此外,由假设1知总扰动F(t)是一致有界的,故系统(7)线性部分的指数稳定性保证了所有参与估计的子系统都是有界的[22].从这个角度上讲,系统(5)将总扰动从原系统(1)中分离出来,并将总扰动引入到指数收敛的系统(7)中,这是本文设计总扰动观测器重要的出发点.

其中k1是和系统(1)、系统(5)相同的可调节系数.对于扰动观测器系统(8),它仅仅取决于ω(1,t),z(1,t),ωxt(1,t)以及zxt(1,t).ω(1,t),ωxt(1,t)与原系统的输入和输出有关,z(1,t)和zxt(1,t)与设计的完全已知系统(5)相关.

定理1通过选择合适的k1>0,将能使系统(10)指数稳定.

证定义Hilbert空间

在H1上,将系统(10)改写为如下发展方程:

基于式(13),定义算子A1的特征值

相关特征函数满足

注意到,针对任意(f,g)T∈D(A1),

经过简单计算,易知算子A1是耗散的且对∀λT∈σ(A1)都有Reλ≤0.又因为所有的特征值均以共轭形式出现,故只需考虑落在第二象限的特征值,即λ=iρ2∈σ(A1)且≤argλ≤π.

对系统(15)直接计算,可得

代入边界f′′(1)的限制条件,ρ需满足下列特征方程:

当Re(ρ)→∞且Im(ρ)是有界时,式(19)具有以下渐进形式:

其中O表示同阶无穷小.式(20)的形式将导致cosρ=

根据算子A1的耗散性,只需证明对∀λ ∈σ(A1),Re(λ)≠0.根据式(14)-(15),有下式成立:

式(23)也能说明Re(λ)≤0.现在证明,式(22)不会存在虚轴上的解,即对∀λ ∈σ(A1),Re(λ)≠0.

假设Re(λ)=0.这里式(14)依然成立,但注意ρ此时设为一个大于0的实数.将式(14)代入式(23),有

将式(25)的边界条件代入式(18),考虑到f(x)非零,有

显然,式(26)对于ρ>0无解.由式(22)和式(26)知,不会存在以0为聚点的特征值,故式(22)不会存在虚轴上的解.

综上所述,通过选择合适的k1>0,能够使λn的实部为负数,且对任意模充分大的本征值都是几何单的.

定理1得证.证毕.

定理2若A1由式(13)定义,则A1能在H1上生成一个C0-半群eA1t.

证 显然,存在A1的广义特征函数构成H1的Riesz基.参考文献[23]Lemma 3.2的证明方法,由本文式(16)可知

定理2得证.证毕.

根据定理2,算子A1能够在H1中生成一个压缩的C0-半群,故存在常数LA1和ωA1>0使得[22-23]

且定义的Φ(τ)满足

简单计算有

根据式(28)(30),易从式(31)中得到

其中:T>0是任意给定的常数,C0为一个和初始条件有关的正数.由(32)可知,当t→∞,xxx(1,t)→0,即

定理3得证.证毕.

推论1系统(8)实际上是作为系统(7)的一个输入观测器.从式(9)的定义可以看出

将系统(7)和系统(8)放在一起

可得完整的扩张状态观测器(34).这样做的优点是没有考虑总误差F(t)的各阶导数,不会引入求导过程中所带来的误差,尤其是与系统状态(ω(·,t),ωt(·,t))相关的非线性求导误差,同时,该观测器的设计也不会带来高增益问题.

4 反馈控制器设计

观察发现,当F(t)≡0时,若设计u0(t)=k2ωt×(1,t)[5],k2>0,可使系统(1)稳定.定理1-3以及式(28)表明,系统(10)将以指数形式收敛,即

设计控制器u0(t)=k2ωt(1,t)-xxx(1,t),此时完整的闭环控制系统为

由定理3分析可知

5 仿真分析

为直观展示本文所介绍的反馈控制器以及扰动观测器,本节采用有限差分法,利用MATLAB进行了一些数值模拟分析.空间步长和时间步长分别为dx=0.05,dt=0.0001,外部干扰d(t)=sint,内部不确定项f(·)=0.5 cos(ω(1,t)).初始值设置为:ω(x,0)=sin(2πx)cos(1.5πx),ωt(x,0)=-0.2x,(x,0)=(x,0)=0,(x,0)=(x,0)=-0.1x,k1=1,k2=8.系统(35)的解决方案绘制在图1-3中,总扰动及其估计值绘制在图4中,控制器u0(t)绘制在图5中.图中各参数的含义分别为:x表示梁的位置,t表示时间,F(t)和xxx(1,t)分别指总扰动和其估计值,误差Error=F(t)-xxx(1,t),控制律u0(t)=k2ωt(1,t)-xxx(1,t).

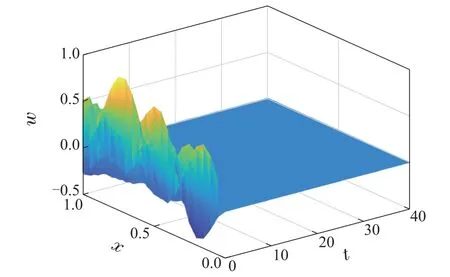
图1 梁的位移ω(x,t)Fig.1 The displacement of the beam ω(x,t)

由图1可以看出,ω(x,t)最终指数收敛至0,符合预期要求.图2和图3证明了所选参考系统和扰动观测器是有界的,并且能够对总扰动起到观测作用.图4表明扰动被有效地估计出来,并且估计误差也在允许范围内.图5展示了边界反馈控制器的输出,可以看出随时间的不断变化,控制器整体输出较为平稳.

图2 参考系统(x,t)Fig.2 The reference system(x,t)

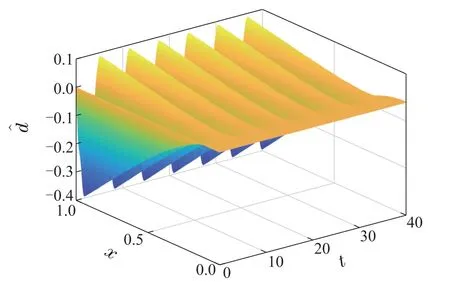
图3 扰动观测器(x,t)Fig.3 The disturbance estimator(x,t)

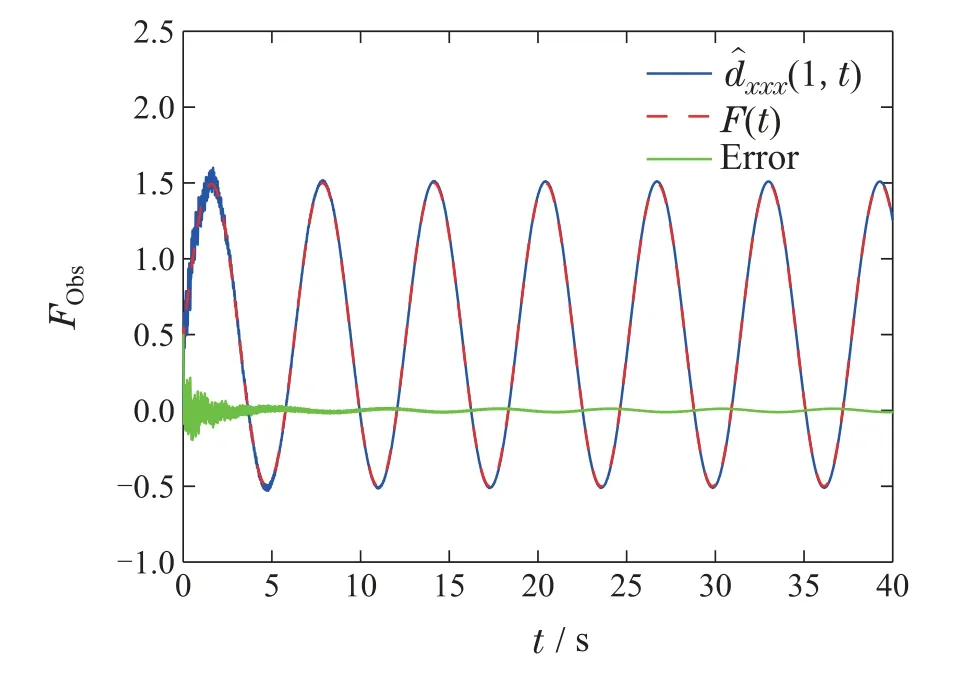
图4 扰动及其估计值Fig.4 The disturbances and their estimates

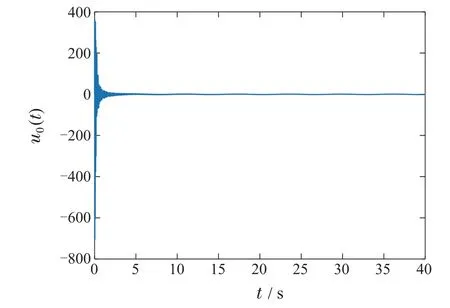
图5 控制律u0(t)Fig.5 The control law u0(t)

6 总结

本文针对一类具有边界扰动、未知外部干扰和内部非线性扰动的Euler-Bernoulli梁方程,设计了干扰观测器,基于文献[5]设计了输出反馈控制器.该控制器的设计过程包括与扰动观测器相关系统的稳定性理论证明、Riesz基理论和无扰动情况下输出反馈控制律3个部分.本文设计的状态观测器无需对干扰求导,也不会引入高增益所带来的种种问题.整个系统的应用仅利用了原系统的输出信号ym,通过控制梁在位置x和时间t即可使整个系统指数稳定.但是,受篇幅限制,一些理论并未展开叙述,详细的推导方法类似于文献[25].

未来,笔者将继续针对Euler-Bernoulli梁方程进行研究,并扩展其在实际领域中的应用.例如,研究带有某些未知参数的Euler-Bernoulli梁方程系统,利用输入-输出关系或二值信息辩识系统的未知参数,进而根据状态构造伺服系统,设计控制器最终实现系统的输出调节.另一方面,结合文献[26-28],该控制理论可考虑应用至手术机器人领域.由于人体腔道的复杂性,柔性机器人在未来一定是手术机器人的不二选择.本文所讨论的Euler-Bernoulli梁作为一个基础梁系统,下一步可根据机器人的机械结构、力学特性和运动特征,构建更加完善的动力学模型,进而设计扰动观测器和边界输出反馈控制器,从而实现机器人在人体腔道内安全稳定运行.