葛富东,陈阳泉,寇春海

(1.中国地质大学(武汉)计算机学院,湖北武汉 430074;2.加州大学默塞德分校机械工程学院(MESA实验室),美国加州95343;3.东华大学数学与统计系,上海 201620)

1 引言

能控性作为现代控制理论研究中一个十分重要的基本问题,最早是由Kalman等在20世纪60年代初针对有限维系统首次提出的[1-2].由于能控性可较好的刻画系统的性能,一经提出便引起了学者们的广泛关注,并很快被推广到了无穷维扩散系统[3-4].与有限维系统的能控性不同,无穷维扩散系统的能控性定义不仅依赖于空间信息,而且与控制时间的长短息息相关,还形式不唯一,常用的有精确能控性、逼近能控性以及零能控性.例如,考察如下无穷维线性扩散系统:

式中:Ω ⊆Rn是一个具有光滑边界∂Ω的有界开子集,T>0是一个常数,z0属于Hilbert空间L2(Ω).此外,算子B是与控制器位置、数量等有关的控制算子,而控制输入u属于Hilbert空间U.为阐述清楚无穷维扩散系统(1)的能控性定义,令集合

为系统(1)在T时刻的能达集,并给出如下定义:

1) 对任意初值z0∈L2(Ω),有GT(z0,u)=L2(Ω)始终成立,则称系统(1)在T时刻是精确能控的;

2) 对任意初值z0∈L2(Ω),GT(z0,u)在L2(Ω)空间内是稠密的,则称系统(1)在T时刻是逼近能控的;

3) 对任意初值z0∈L2(Ω),能达集GT(z0,u)中含有0,则称系统(1)在T时刻是零能控的.

更多关于无穷维扩散系统能控性问题的研讨,请参见文献[5-9].

进一步地,为突出空间信息对系统能控性的影响,子区域能控性问题顺势被提出[10-13].假设ω ⊆Ω是一个给定的非空区域,引入投影算子

本文有如下子区域能控性定义[12-13]:

I)如果对任意初值z0∈L2(Ω),有

成立,则称系统(1)在T时刻ω区域上是子区域精确能控的;特别的,由于0∈L2(ω),若0∈χωGT(z0,u),则称系统(1)在T时刻ω区域上是子区域零能控的;

II)如果对任意初值z0∈L2(Ω),使得χωGT(z0,u)在空间L2(ω)内是稠密的,则称系统(1)在T时刻ω区域上是子区域逼近能控的.

根据算子χω的定义,当ω=Ω时,子区域能控性退化为经典有界区域上的能控性.因此,子区域能控性定义可视为经典有界区域上能控性定义的一种推广.

另一方面,自20世纪80年代以来,随着科学技术的不断发展,人们逐渐发现了越来越多的不能用传统的整数阶扩散系统来解释或进行建模的所谓反常扩散现象,如污染物在地下水中的迁移和漂流、高温高压下等离子体的迁移运动等[14-16].这些反常扩散现象因不再遵循高斯统计规律和Fick定律且具有历史依赖性,使得其运动过程不能用由局部极限所定义的整数阶导数予以精准建模描述.注意到反常扩散微粒的均方位移表现为如下的幂律函数依赖关系[17]:

式中:r表示粒子的扩散半径,〈r2(t)〉表示区域内所有粒子扩散半径的平方的集平均(ensemble average)1更多关于集平均的介绍,可参见链接: https://en.wikipedia.org/wiki/Mean_squared_displacement.,t为扩散时间,α>0为反常扩散指数且kα为反常扩散系数,而布朗运动中微粒的均方位移仅为关于时间t的线性函数关系

这里k1>0为一个常数.所以,为更精确地刻画反常扩散过程,研究人员需寻求新的数学物理建模工具.

为实现这一目的,本文追溯伟大物理学家A.Einstein在文献[18]中的结果.在该文献中,Einstein从微观尺度的角度,详细阐述了整数阶扩散系统与布朗运动之间的数学推导关系.在此基础上,注意到作为整数阶导数推广的分数阶导数,实际上是一个微分-积分卷积算子,具有非局部性质,其定义充分体现了系统变量发展的历史依赖性[19-20].因此,在文献[21-24]研究结果基础之上,本文拟引入连续时间随机游走模型对反常扩散过程进行研究,力图驱动产生不同情形下的分数阶扩散系统,并在剖析和综述这些分数阶扩散系统能控性、子区域能控性领域最新研究成果的同时,提出前沿性研究机遇和挑战.

2 预备知识

2.1 分数阶微积分基本理论

为更好的综述分数阶扩散系统的子区域能控性研究进展,本部分首先介绍一些基本的分数阶微积分定义和性质,更多相关内容的阐述,请参见该领域内的经典专著[25-29].

定义1[27-28]假设函数f ∈L1(0,∞),α>0.函数f的α阶Riemann-Liouville分数阶积分定义为

类似于经典积分算子,Riemann-Liouville分数阶积分同样满足如下半群性质[27-28]:

基于积分与微分运算的互逆性,分数阶导数一般有两种基本方式: 一种是“先积分再微分”的Riemann-Liouville分数阶导数,另一种是“先微分再积分”的Caputo分数阶导数.

定义2[27-28]假设函数f ∈L1(0,∞),则f的α阶Riemann-Liouville分数阶导数定义为

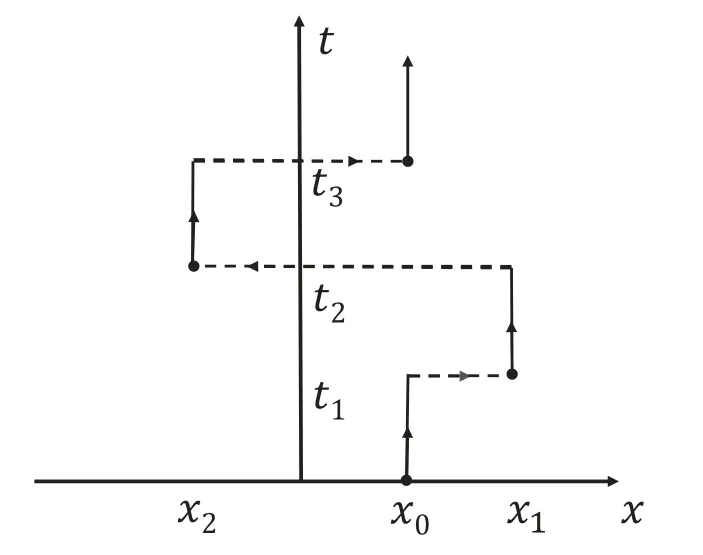
式中:n-1<α

定义3[27-28]假设函数f ∈ACn[0,∞),那么f的α阶Caputo分数阶导数定义为

式中:n-1<α

注1定义3中的f ∈ACn[0,∞)表示f在任意闭区间[0,T]⊆[0,∞)上有直到n-1阶连续导数且满足f(n-1)∈AC[0,T].这里AC[0,T]指闭区间[0,T]上的绝对连续函数空间.根据文献[30]中的338页,若f ∈AC[0,T],则存在函数φ ∈L1(0,T)和常数c使下式成立:

因此,绝对连续函数f(t)在区间[0,T]几乎处处有可和导数满足φ(t)=f′(t).

一般情况下,分数阶微分算子不具有半群性质,但满足下面的结论.

根据引理1和引理3,Riemann-Liouville分数阶导数和Caputo分数阶导数均为分数阶积分的左逆算子.由式(13)可知,含Riemann-Liouville分数阶导数的分数阶微分方程初值问题的初始条件必须是函数的Riemann-Liouville分数阶导数在零点的取值.然而,到目前为止,Riemann-Liouville分数阶导数的物理意义尚不明确,所以Riemann-Liouville分数阶导数不便用于工程与物理建模.此外,根据式(15),Caputo分数阶导数成功规避了这一弊端,其微分方程初值问题的提法可与经典的提法一致,为函数的整数阶导数,具有明确的物理意义.因此,Caputo分数阶导数定义更适于实际工程问题研究的需要.

2.2 分数阶扩散系统模型

如图1所示,在运用连续时间随机游走理论刻画自然界或工程中的反常扩散过程时,假设任意两个相邻跳跃长度或等待时间之间的概率函数是ψ(x,t),则跳跃长度概率密度函数λ(x)和等待时间概率密度函数σ(t)可分别定义为

图1 连续时间随机游走模型Fig.1 Continuous time random walk(CTRW)model

据此,λ(x)dx表示粒子在区间(x,x+dx)内跳跃的概率,而σ(t)dt表征粒子在区间(t,t+dt)内等待的概率.令z(x,t)为粒子在t时刻x位置处的概率密度函数.根据文献[22,31-32],则有

为粒子在t时刻到达x位置处的概率,δ(·)为表征粒子初始条件的狄拉克δ函数且下式成立:

根据Laplace变换的性质[33],有

表示ϕ(·,t)关于变量t的Laplace 变换.为确定函数(x,s)的具体表达式,根据式(19),若初值条件设定为z0(x),通过对函数η(x,t)中的变量t进行Laplace变换,对其x变量进行Fourier变换,有

表示函数ϕ(x,·)关于变量x的Fourier变换.更多关于无穷维系统Fourier变换的阐述,请参见文献[34].综上,z(x,t)满足如下代数关系:

情形1假设上述概率函数ψ(x,t)=λ(x)σ(t)可时空分离且下式成立:

若等待时间概率密度函数σ(t)=exp(-t),即

据此,根据逆Fourier 变换和逆Laplace 变换的性质[33-34],可知z(x,t)满足如下经典整数阶扩散系统:

在研究如何由式(25)驱动产生分数阶扩散系统之前,首先引入如下双变量Mittag-Leffler特殊函数(简称: Mittag-Leffler函数)[35]:

表1 Mittag-Leffler函数的Laplace变换Table 1 A list of Laplace transformation for Mittag-Leffler function

若等待时间概率密度函数σ(t)=tα-1Eα,α(-tα),其中α∈(0,1]是一个常数,根据表1,可得

代入到式(31)中,则有下式成立:

因此,基于逆Fourier变换以及表1中逆Lapalce变换的性质,z(x,t)满足如下时间分数阶扩散方程:

同上,若等待时间概率密度函数为

成立.为此,引入如下分数阶Laplace算子[36-37]:

是一个仅与n,β有关的常数且算子(-∆)β满足如下Fourier变换的性质[38-39]:

据此,类似的,根据表1,可得概率密度函数z(x,t)分别满足如下空间分数阶扩散方程:

和如下时空分数阶扩散系统:

综上,尽管时至今日分数阶微积分的研究仍有许多数学理论悬而未决,但由于分数阶微积分算子具有独特的性质,克服了经典整数阶模型理论和实验结果吻合不好的缺点.从微观意义上讲,分数阶微积分能被用来描述那些具有非高斯、幂律衰减等特征的亚扩散过程和超扩散过程[13,17,22].从宏观意义上讲,分数阶扩散系统可描述那些无法用整数阶扩散系统精准刻画的运动过程,如细胞在组织中运动,污染物在地下水中的扩散等.因此,对分数阶扩散系统控制理论和应用方面的研究具有重要的现实意义.接下来,本文将对分数阶扩散系统的能控性、子区域能控性研究进展予以综述,以展望该领域的前沿性认识和研究思路.

3 分数阶扩散系统子区域能控性分析

根据第2.2小节,本部分拟通过综述时间分数阶扩散系统、空间分数阶扩散系统以及时空分数阶扩散系统的子区域能控性研究进展介绍本文的主要研究成果.

3.1 时间分数阶扩散系统的子区域能控性研究

时间分数阶扩散系统隶属于无穷维系统范畴,根据文献[40-41],其控制器类型一般分为分布式控制器与边界控制器两类.然而,目前该方面的研究主要集中于分布式控制器作用下的情形,而且对于边界控制控制器作用下的情形,根据文献[42],可基于分数阶分部积分公式将其等价转化为分布式控制的情形.因此,本小节将专注于综述分布式控制器作用下时间分数阶扩散系统子区域能控性问题的研究进展.此时,被研究系统可被写为如下发展方程的形式:

式中:A是Hilbert空间L2(Ω)中的一无界线性算子,B为控制算子,u属于Hilbert空间U表示控制输入.

在时间分数阶扩散系统经典能控性研究方面,据作者所知,大多数是从方程的角度、利用解的表达式来实现的.若算子A可生成一个C0半群,El-Borai于2002年首次利用概率密度函数结合Laplace变换,给出了其解的表达式[43].据此,许多学者利用算子半群和不动点定理建立了分布式控制器作用下时间分数阶扩散系统逼近能控性的充分条件判定定理,如广西民族大学的刘振海教授[44]、湘潭大学的周勇教授[45-46]、贵州大学的王锦荣教授[47-48]、土耳其詹卡亚大学的D.Baleanu[49]以及葡萄牙阿威罗大学的D.F.M.Torres[50]教授等.此外,若系统算子的特征值、特征函数可知且控制算子有界时,文献[42]推广Fattorini准则建立了可保证时间分数阶扩散系统逼近能控性的充要条件判定定理.

在子区域能控性研究方面,当系统算子的特征值、特征函数已知时,通过综合运用分数阶微积分理论、泛函分析工具以及无穷维系统控制理论,作者于2016年在文献[11]中分别建立了分布式控制器作用下线性时间分数阶扩散系统子区域精确能控性与子区域逼近能控性的充要条件判定定理,并研究了与之相关的最优控制问题.随后,在文献[51]中推广探讨了线性时间分数阶扩散系统的子区域梯度能控性,并分别给出静态点控制器、区域控制器与线控制器需满足的配置条件.葡萄牙阿威罗大学的D.F.M.Torres等推广研究了时间分数阶扩散系统的子区域扩展能控性问题[52].最近,作者在文献[53]建立了半线性时间分数阶扩散系统子区域逼近能控性的充分条件判定定理及与之相关的最优控制问题,并将所得结果应用于疾病传播防治问题中去.

3.2 空间分数阶扩散系统的子区域能控性研究

空间分数阶扩散系统因能更有效地描述自然界或工程中比布朗运动快的超扩散过程,如爆炸过程,踩踏现象等而引起了学者们的极大兴趣[22,54-55].根据文献[39,56],此时,被研究系统可分为如下两种情况:

式中:Ω ⊆Rn为一个具有光滑边界∂Ω的有界开子集,T>0是一个常数,-(-∆)β,β∈(0,1]表示分数阶Laplace算子,B为控制算子,u ∈U为控制输入.这里式(45)表示分布式控制器作用下的情形,而式(46)为含边界控制输入的情形.

由于分析空间分数阶扩散系统的控制问题需综合运用泛函分析、无穷维系统控制理论等较为高深的数学工具,导致了其能控性问题的研究一直未被探讨.直到2006年,Micu 与Zuazua 在文献[38]中首次运用Fourier级数建立了可保证一维线性空间分数阶扩散系统零能控性的充分条件判定定理.同年,Miller教授在文献[57]中从抽象分析的角度,基于空间分数阶扩散系统解的表达式以及算子理论给出了线性空间分数阶扩散系统零能控性的判定定理.因为该研究方法主要是从零能控性的定义出发,基于算子理论实现的,一经提出便引起了学者们的广泛关注.在此基础上,四川大学的吕琦教授研究了空间分数阶扩散系统的Bang-Bang 原理,并且据此分析了被研究系统的零能控性[58].Biccari与Hernandez-Santa-maria在文献[59]运用Hilbert 唯一性方法详细研究了一维空间分数阶扩散系统的零能控性和逼近能控性问题,并设计具体的策略求解了与它们相关的最优控制问题.

为突出区域特征对空间分数阶扩散系统能控性研究的重要性,在子区域能控性研究方面,作者于文献[39]中基于分数阶Laplace算子的特征值理论,运用Hilbert唯一性方法最早建立了分布式控制器作用下可保证线性空间分数阶扩散系统子区域逼近能控的充要条件判定定理,并求解了与之相关的能耗最小最优控制问题.最近,基于分数阶Lapalce算子的特性,还进一步研究了边界控制输入作用下线性空间分数阶扩散系统的子区域逼近能控性问题[56].

3.3 时空分数阶扩散系统的子区域能控性研究

由于时空分数阶扩散系统更为复杂,对其能控性问题的研究也一直悬而未决,直到2018年,Sonawane与Kumar首次基于系统算子的矩理论以及算子半群理论研究了一维时空分数阶扩散系统的零能控性问题[60].随后,美国波多黎各大学的Warma教授在文献[61]中推广研究了如下高维时空分数阶扩散系统的逼近能控性问题:

这里Ω ⊆Rn为一个具有光滑边界∂Ω的有界开子集,T>0是一个常数,O⊆Ω是一个非空开子集,0<α≤1,0<β≤1且u(x,t)表示外部控制输入.具体的研究内容如下: 首先,根据半群理论和分数阶导数的特性,推广文献[43]中的结果,得到时空分数阶扩散系统(47)解的具体表达式;其次,深入分析分数阶Laplace算子的特性,得到一些有用的引理,如分数阶分部积分公式以及一些不等式;然后,推广构建时空分数阶扩散系统的唯一延拓定理,并据此得到时空分数阶扩散系统逼近能控性的充分条件判定定理.

最后,需指出的是,据作者所知,时至今日,时空分数阶扩散系统的子区域能控性问题尚未被研究.

4 结论

近年来,随着分数阶微积分理论的不断发展及其与控制科学的深度交叉融合,分数阶扩散系统的能控性、子区域能控性问题引起了人们的广泛关注,并取得了一定的研究成果.鉴于此,本文分3个方面对该领域的研究进展予以了综述.然而,目前该课题的研究仍处于初级阶段,尚有大量问题亟待解决:

1)非线性分数阶扩散系统的能控性/子区域能控性.

目前无论是时间分数阶扩散系统、空间分数阶扩散系统还是时空分数阶扩散系统,其能控性/子区域能控性问题研究中的模型都是线性的.然而,在实际应用中,许多反常扩散过程都是非线性的,如污染物质在地下水中传输、药物在人体内运动等.由于非线性分数阶扩散系统相对于其线性情形具有更为复杂的动力学特性,很多线性系统的研究方法和工具将不再适用.因此,需发展新的研究方法或工具对其进行研究.此外,如何推广线性分数阶扩散系统的相关研究成果至非线性分数阶扩散系统的情形,也是现阶段该课题一个重要的研究方向,且已取得了初步的研究成果.

2)有限维控制器作用下分数阶扩散系统的子区域能控性.

有限维控制器的引入可有效地克服无穷维控制方式难以应用于实际控制问题的不足,相关研究可更具针对性的给出控制器的配置策略[62].而且,Khapalov在经典文献[63]中已经证明: 作用于整数阶扩散系统且满足一定条件的两个移动点控制器可实现无穷维控制器的控制效果.在此基础上,作者在有限维静态控制器作用下线性时间分数阶扩散系统以及线性空间分数阶扩散系统的子区域能控性方面已取得了初步的研究成果[11,13,39,56].因此,有必要在有限维静态控制作用下非线性时间、空间以及时空分数阶扩散系统的子区域能控性领域做更进一步的探索.

3)分数阶扩散系统的广义能控性/子区域能控性.

最近,整数阶反应扩散系统的完全能控性[64]、扩展能控性[65]、梯度能控性[66]等广义能控性问题已取得了研究突破,并应用于具体的实际问题中.因此,如何引入新的数学工具,基于分数阶微积分理论,探讨线性分数阶扩散系统和非线性分数阶扩散系统的广义能控性以及广义子区域能控性问题,具有重要的研究意义.

4)分数阶扩散系统的离散能控性/子区域能控性.

离散控制输入的引入,可实现减少控制输入次数、节约资源的目的.目前,离散采样控制器作用下有限维系统能控性问题的基本理论已在文献[67]被详细地探讨.在此基础上,南京航空航天大学的杨浩教授等[68]推广研究了整数阶无穷维线性系统的离散近似能控性和离散精准能控性问题.此外,作者在文献[23-24]还分别探讨过时间分数阶扩散系统的分布式事件触发控制离散问题和边界事件触发离散控制问题.然而,据作者所知,目前关于分数阶扩散系统离散能控性/子区域能控性问题的研究还没有结果呈现.但随着数字控制技术的不断发展与成熟,大多数控制问题的实现需转化为离散控制输入的情形.所以,分数阶扩散系统离散能控性、离散子区域能控性问题的研究十分重要.

5)控制器的优化配置问题.

控制器的配置情况将直接影响其性能的发挥,进而影响系统的整体控制效果.如何优化配置分数阶扩散系统能控性问题研究过程中的控制器,具有重要的研究意义.为此,作者在文献[69]中,通过综合运用分数阶微积分理论、无穷维系统控制理论,创新性的构建了分数阶Fisher信息矩阵,对时间分数阶扩散系统的控制器优化配置问题予以了回答.鉴于此,如何推广研究线性空间/时空分数阶扩散系统,以及非线性分数阶扩散系统的控制器优化配置问题将是未来需探究的课题.

6)分数阶扩散系统能控性/子区域能控性方法的实际应用.

近20年来,分数阶模型在固体力学、流体力学、粘弹性力以及生物工程等中取得了很好的应用[16,70-74].众所周知,理论研究成果可借助于实际应用开展有效性验证,反之,实际应用亦可促使学者们提出新的科学问题,进而推动理论研究的发展.因此,在未来,如何落实实际的应用场景,并利用分数阶扩散系统的能控性/子区域能控性方法来解决其中的控制问题,值得进一步的研究.