白绍强

摘  要：从2022年中考天津卷第18题的解题思路入手，挖掘如何将作图方法和运算、推理有机结合. 通过去除网格和圆，引导学生把握问题的实质，厘清知识内在的脉络和逻辑关联；通过改变圆的位置和大小或隐去圆，凸显网格的作用等途径，变化作图工具，创新网格作图题．

关键词：逻辑关联；基本策略；推理计算

在正方形网格中用无刻度的直尺作图的试题，在近几年各地区的中考试卷中频繁出现，逐渐成熟且日趋完善，成为独具特色的中考试题. 网格作图题立意新颖且内涵丰富. 其考查内容可涉及勾股定理、特殊图形的性质、平行线分线段成比例、相似、图形的变化（平移、轴对称、旋转）等，对学生的能力要求较高. 学生往往会想不到画法，看了答案也不懂. 究其原因，是学生没有理解隐含在网格背后的大量的推理与计算. 只有将作图方法和运算、推理有机结合，才能明白作图方法是怎么想出来的，才能了解作图原理，积累网格作图的一般方法和基本经验，进而从不同视角尝试解决问题．

一、试题呈现

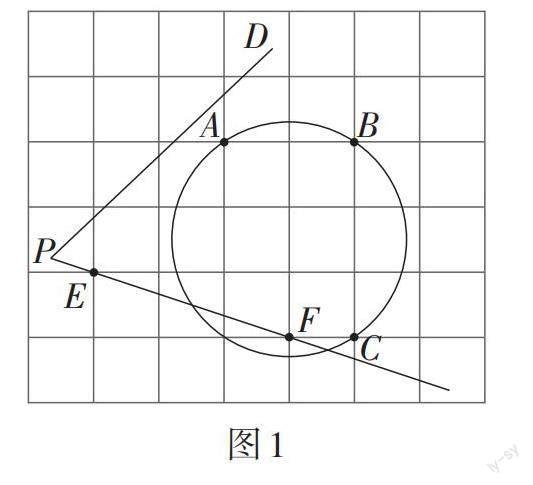
题目 （2022年天津卷）如图1，在每个小正方形的边长为1的网格中，圆上的点A，B，C及[∠DPF]的一边上的点E，F均在格点上．

（1）线段[EF]的长等于__________；

（2）若点M，N分别在射线[PD]，[PF]上，满足[∠MBN=90°]且[BM=BN]，试用无刻度的直尺，在如图1所示的网格中，画出点M，N，并简要说明点M，N的位置是如何找到的（不要求证明）__________     ．

本文主要基于此题的第（2）小题，探究网格作图题的解题路径，并创新网格作图题.

二、厘清问题逻辑结构

去除网格和圆，发现问题的实质是在[∠DPF]的内部有一点[B]，要在[∠DPF]的两边上分别找到点M，N，使得[△MBN]为等腰直角三角形. 基于点E，F在网格中的位置关系，可以联想到以下两个熟悉的基本图形，进而转化问题.

基本图形1：如图2，[P]是[∠AOB]的平分线上一点，[PC⊥OA]，[PD⊥OB]，垂足分别为点[C]，[D]，点[M]，[N]分别在边[OA]，[OB]上，当满足[∠MPN=∠CPD]时，易证[△CPM]≌[△DPN]. 所以[PM=PN]．

基本图形2：如图3，[D]为正方形[ABCD]的顶点，点M在边[AB]上，点[N]在边[BC]的延长线上，当满足[∠MDN=90°]時，易证[△ADM≌△CDN≌]. 所以[DM=DN].

对图3进行分析，题目中满足要求的点[M]应该在正方形的边与射线[PD]的交点处. 其等同于：如图4，已知在[∠AOB]内有一点[P]，四边形[PCED]为正方形，点[C]，[E]在边[OB]上，[DE]与边[OA]相交于点[M]，当满足[∠MPN=90°]时，有[PM=PN]．

还可以从图形变化的角度进行思考，将[PN]绕点[P]顺时针旋转[90°]得到[PM]. 将[PC]作同样的旋转得到[PD]，易得[△DPM]≌[△CPN]. 所以[DM=CN]. 反之亦然.

三、寻找作图的一般方法

无论是尺规作图，还是网格作图，其关键点都在于作图方法是怎样想到的，需要经历怎样的思维过程，以及解决此类问题的一般方法是什么. 逆向思维、执果索因、反其道而行之是解决此类问题的基本策略．

1. 假设已有图形，进行几何构图

先想象出符合要求的图形，然后画出草图，并适当添加线段进行可能的几何构图. 如图5，假设图中的[BM]，[BN]满足题设要求. 注意到图中的[EF]和[BF]具有特殊的数量关系和位置关系，易想到[△EFB]为等腰直角三角形，[EB]是直角的平分线，四边形[EFBQ]为正方形. 在此基础上，通过多方联想，调用学生的已有经验，构造特殊图形和基本几何模型成为解决问题的关键．

2. 分析图形特征，展开逻辑推理

引导学生分析当前图形具有的性质和题设中的已知条件，明晰差距，寻找问题解决的策略. 此题的图形特征包括：点[M]在正方形EFBQ的边[EQ]上，[BQ=][BF]且[∠FBQ=][90°]，[QM=FN]. 我们要认真分析通过已知条件可以得到什么结论，得到的结论和最终的解题目标之间还差什么，如何进一步满足. 经过这样的分析，可以确定如下的作图思路：过点[B]作[BF]的垂线[BQ]；在垂线[BQ]上截取[BQ=BF]；过点[Q]作[BQ]的垂线，交射线[PD]于点[M]；过点[B]作[BN⊥BM].

3. 抓住问题本质，回归基本作图

作图过程要和推理证明过程一样有理有据，只有理解了作图原理，聚焦作图方法和几何推理，才能将问题转化为基本作图，才能知道法自何处、学为何用，才能清楚每一步作图的方法、程序，具体操作的理论依据、意图和目标方向. 学生对于在网格中作平行线、垂线、线段中点或[n]等分点等基本作图应熟练掌握.

四、创新网格作图题

1. 改变圆的位置和大小

网格作图和尺规作图一样，都是通过交轨法确定特殊点. 因为点的确定需要两条直线相交，所以需要先分析点的位置特征，来确定经过点的两条直线满足的条件，思考画出怎样的两条直线才能作出符合条件的点，再借助网格确定相应的画法．

圆中有许多重要的性质，如垂径定理和圆心角与圆周角的关系等. 因为直径所对的圆周角是直角，所以圆可以为画两线垂直带来方便. 圆心是圆中的重要要素，圆的许多性质都与圆心和半径有关. 那么，如何确定圆的圆心呢？如图6，连接[AC]，交网格线于点[O]. 根据[90°]的圆周角所对的弦是直径，可以确定AC是圆的直径，则点[O]即为圆心. 或者根据两条直径的交点为圆的圆心，可以取格点[G]，连接[AC]，[BG]，相交于点[O]，则点[O]即为圆心， 如图7所示．

题目给出了经过[A]，[B]，[C]三点的圆，降低了难度，给学生解题带来了方便. 如果改变条件，给出过[B]，[F]两点的圆或只过一点[B]的圆，其实也不影响题目的解答，问题求解的关键仍然是确定圆心.

如图8，当圆经过点[B]，[F]时，根据过两点的圆的圆心在两点所连线段的垂直平分线上，取格点[S]，[T]并连接. 设圆与网格线相交于点G，H，连接[GH]，[ST]，相交于点[O]，则点[O]即为圆心.

如图9，当圆只经过一个点[B]时，要想确定圆心，则需要构造另外一个[90°]的圆周角. 取格点S，T，连接[SB]，与圆相交于点[R]，连接[BT]并延长，与圆相交于点[K]，连接[RK]，[GH]，相交于点[O]，则点[O]即为圆心．

2. 隐去圆，凸显网格作用

学生熟练掌握网格中的基本作图方法后，面对千变万化的问题情境也能应对自如. 此题若隐去圆，能否充分发挥网格的作用完成作图？

正方形网格中蕴含着丰富的数量关系、位置关系和特殊图形，依据特殊图形的性质，通过计算和推理可以画出特殊位置的直线和一定长度的线段，并确定由它们相交而产生的特殊点．

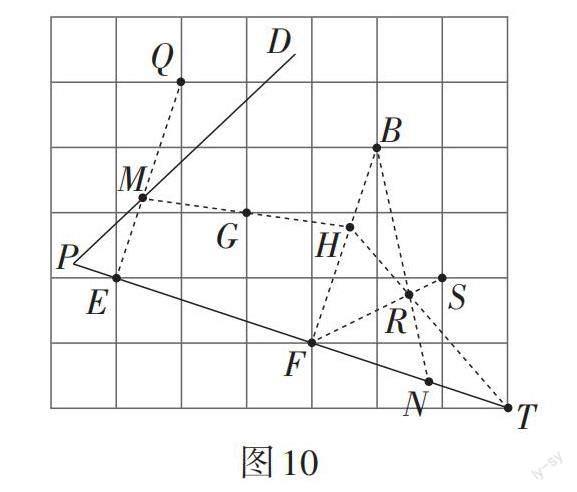
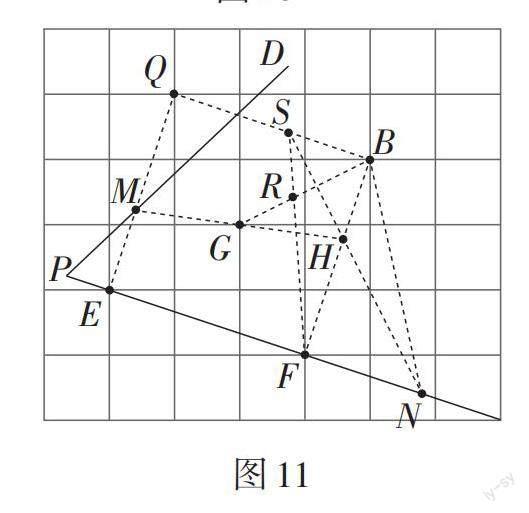
如图10，注意到已知条件中的线段[EF]，[BF]具有特殊的数量关系和位置关系——[EF=BF=10]，[EF⊥BF]，易想到等腰直角三角形[EFB]和正方形[EFBQ]这两个特殊图形. 取格点[G]，其是正方形的中心，这为后面应用正方形的中心对称性奠定了基础. 连接[MG]并延长，交[BF]于点[H]，易证[MQ=FH]. 只要再满足条件[FN=][FH]，问题就可以得到解决. 取格点[T]，则[△BFT]为等腰直角三角形，利用等腰三角形的轴对称性，取格点[S]，连接[FS]，只需要对称地取点、对称地连线. 连接[HT，FS，] 相交于点[R]；连接[BR]并延长，与射线[PF]相交于点[N]. 由[△BHR]≌[△TNR]，得[BH=TN]. 所以[FH=FN]. 图11的作图思路与此类似．

要满足[FN=FH]，也就是[△HFN]为等腰直角三角形，只要一角等于[45°]即可. 考虑到正方形的对角线分直角有[45°]，故可以画出正方形对角线的平行线. 如图12，取格点[S]，[Q]，[G]，连接[SG]，[QG]，[QG]与网格线相交于点[T]. 连接[MT]并延长，与[SG]相交于点[R]. 连接[RH]并延长，与射线[PF]相交于点[N]. 连接[QR，] 由[MQ∥GR]且[MQ=GR]，得四边形[QMGR]是平行四边形. 所以[QR∥GH]且[QR=GH]. 所以四边形[QGHR]是平行四边形. 所以[RN∥QG]. 所以[∠FNH=45°].

图13和图14给出了两种作对角线的平行线的方法，其意图仍然是作正方形对角线的平行线，使[∠FHN]或[∠FNH]等于[45°]，得到[FN=FH=QM]这一重要条件，其原理不再一一赘述．

3. 改变点的先后确定顺序

事实上，射线[PD]绕点[B]逆时针旋转[90°]后，与射线[PF]的交点即为点[N]. 如图15，取[PD]与网格线的一个交点[J]，[BR]为[∠GBK]的平分线且[∠GBK]= 90°，连接[JK]与[BR]相交于点[I]，連接[GI]并延长交网格线于点[H]，则点[J]绕点[B]逆时针旋转[90°]后得到点[H]. 如图16，取[PD]与网格线的另一个交点[R]，连接[JK]，[RW]相交于点[I]，连接[GI]并延长与网格线相交于点[L]，连接[LS]并延长与网格线相交于点[T]，则点[R]绕点[B]逆时针旋转[90°]后得到点[T]. 连接[TH]并延长与[PF]相交于点[N]，再借助圆心[O]，仿照前面提及的步骤，点[M]的位置也随之确定．

五、网格作图题的教学策略

1. 教会学生思考，发展学生的思维能力

网格作图题不同于给定已知条件、给出图形的计算题或证明题，需要认真分析目标图形与现有条件之间的差距，构造几何图形，通过相关计算与证明，探求得到作图方法. 网格作图题往往涉及的知识面较广，具有挑战性，学生会感到无从下手，找不到解决问题的切入点或突破口，成为教学的一个难点. 对于网格作图题的求解，学生不仅需要知道作图的先后程序步骤，还需要知道这样作图的道理，更需要知道这样作图的方法是怎么想到的. 正如在解题过程中需要阐明解题思路一样，在网格作图题中，教师要引领学生经历作图思路的获得过程，感悟作图内在的本质. 在作图题的教学中，如果教师只是让学生按作法动手操作，只关注作图方法的先后程序，而忽视作图问题与几何推理的密切结合，则学生无法掌握作图题的操作本质，也无法自主解决新的作图问题. 乔治·波利亚指出，数学教育的主要目的之一是教会学生如何思考问题，发展学生解决问题的能力，关注学生的深度思考过程. 因此，教师要把握好在网格作图方法探寻过程中发展学生思维品质的契机．

2. 一般观念指引，关注作图通法

数学内容的学习要让学生获得研究套路和研究方法，使学生能自觉运用一般观念指导数学学习与探究活动. 章建跃博士指出，一般观念是对内容及其反映的数学思想和方法的进一步领悟、提炼和概括，是对数学对象的一般性回答，对学生学会用数学的方式对事物进行观察、思考、表达，以及发现和提出数学问题等都具有指路明灯的作用. 学生只有学会运用一般观念、一般方法分析和解决问题，才能实现思维的跨越，这是学生学会学习的标志. 在网格作图的过程中，学生要经历画出目标图形、分析目标图形特征、构造图形、推理论证作法的合理性、分步转化基本作图等过程，这也是几何作图的一般方法，其能够使学生形成作图思路分析的一般方法. 即使是不同的作图方法之间也存在相通的意图和本质属性. 因此，对于作图题，要关注作图的通性通法，适度寻找最优解法和巧妙解法，从思维的正常历程探索解决策略，从通性通法中寻找问题解决的必然思路．

3. 重在推理计算，体会数学的严谨性

对于作图题，教师要引领学生思考并表达作图的合理性，确认作图的准确性，做到言必有据、自圆其说，养成讲道理、有条理、重论据、合乎逻辑的思维习惯. 要在构造图形、应用性质、感悟原理、探析作法的过程中培养学生的空间观念和创新意识，发展学生的空间想象力，提高学生的计算能力和推理能力，促使学生形成敢于质疑的科学态度和理性精神．

正如华罗庚先生所说：数缺形时少直观，形少数时难入微. 这就是数形结合思想. 一些数学内容具有数与形两个方面的特征，以网格为背景建立平面直角坐标系，就可以用坐标来确定点的位置，可以利用一次函数和三角函数的知识来解决长度、距离、交点等代数问题，以及平行、垂直等几何问题，进而引导学生感悟数量关系和图形位置关系的内在联系，这也就是常说的“先算后画”．

网格作图题内涵丰富，思维含量高，奥妙无穷，学生可以经历从不同角度寻求分析问题和解决问题的方法的过程，体验解决问题方法的多样性，充分展现综合能力. 网格作图题要求学生从已有的经验和知识基础出发，通过自然的思维驰骋和深入的画法探析，激发学生独立思考，促使学生积累基本活动经验，形成适应未来发展的数学核心素养．

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］鲍建生，章建跃. 数学核心素养在初中阶段的主要表现之三：几何直观［J］. 中国数学教育（初中版），2022（7 / 8）：3-9．

［3］ 章飞. 几何作图的教学功能分析［J］. 中学数学教学参考（中旬），2021（1）：10-12，19.

［4］ 金杨建. 正方形网格作图的原理、教学功能与建议［J］. 中学数学教学参考（中旬），2021（7）：37-40.