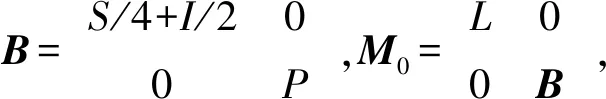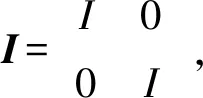Weyl定理与(R)性质的判定
2023-06-13赵巨涛曹小红
赵巨涛,曹小红,董 炯
(1.长治学院数学系,长治 046011;2.陕西师范大学数学与统计学院,西安 710119)
线性算子谱理论问题是泛函分析中的重要内容,在有限维空间中,算子的谱其实就是该算子的所有特征值,即算子的谱为该算子的点谱。而无限维空间中算子的谱是该算子特征值的推广,不仅包括算子的点谱,还包括连续谱与剩余谱。算子谱理论不仅在现代数学、计算数学等数学学科中有着直接的应用(比如求微分方程的特征值问题),而且在物理学中也有着浓厚的研究背景,比如求物体振动的频率、判定系统的稳定性都与算子的局部谱结构紧密相关。近年来,许多谱理论学者将谱理论应用到量子力学研究中,如:利用谱的特点刻画量子计算的表达方式;根据谱的结构特征刻画量子门的上下确界等问题。因此,算子谱结构的研究对物理学等学科的发展具有重要意义。
1909年,WEYL[1]发现了Hilbert空间中自伴算子的Weyl谱恰好等于该算子的谱除去有限重的孤立特征值,这一结论被称为Weyl定理。随后,学者们将Weyl定理进行了变型和推广,将Weyl定理变型为Browder定理、(ω)性质等[2-4],这些变型的Weyl定理反映了算子局部谱的结构特征,统称为Weyl型定理。如:文献[3]研究了线性算子(ω)性质,刻画了与单值延拓性质有关的局部谱的结构特征;文献[4]研究了线性算子的Browder定理与拓扑一致降标有关的局部谱之间的关系。之后,线性算子的Weyl型定理的研究被推广到算子函数中,如文献[5]研究了算子函数的a-Weyl定理((ω)性质)与线性算子a-Weyl定理((ω)性质)之间的关系。近年来,学者们又将目光聚焦到上三角算子矩阵的局部谱问题上[6-8]。如:文献[6]研究了上三角算子矩阵的本质逼近点谱与主对角线上元素算子的联系,并且讨论了上三角算子矩阵的Weyl定理与主对角线上元素算子局部谱之间的关系。
关于Weyl型定理的研究还有许多成果[9-12],但是,这些研究通常仅讨论某一种Weyl型定理的相关问题。近年来,(R)性质(Weyl定理的一种变型)得到了学者们的广泛关注[13-15],本文将对有界线性算子及上三角算子矩阵的Weyl定理和(R)性质的关系进行首次讨论。首先,给出有界线性算子同时满足(R1)性质和Browder定理(或者(R)性质和Weyl定理)的充要条件;其次,刻画上三角算子矩阵同时满足(R1)性质和Browder定理(或者(R)性质和Weyl定理)的条件。
1 预备知识
asc(T)=inf{n:N(Tn)=N(Tn+1)},
des(T)=inf{n:R(Tn)=R(Tn+1)}。
若这样的整数不存在,则记asc(T)=∞或者des(T)=∞。若R(T)闭且n(T)<∞,则称T是上半Fredholm算子;特别地,若T为n(T)=0的上半Fredholm算子,则称T为下有界算子。若d(T)<∞,则称T是下半Fredholm算子;特别地,当d(T)=0时,称T为满算子。若T既是上半Fredholm算子又是下半Fredholm算子,则称T是Fredholm算子。若算子T是半(上半或下半)Fredholm算子,则可以定义T的指标为
ind(T)=n(T)-d(T)。
若T为Fredholm算子且ind(T)=0,则称T为Weyl算子;若T为Weyl算子且升标或降标有限,则称T为Browder算子。易证T是Browder算子当且仅当T为半Fredholm算子且T可逆或者0为T的谱的孤立点。
若集合E⊆,用isoE、accE、intE分别表示集合E的孤立点的全体、聚点的全体、内点的全体。若V为H的子空间,记V⊥为V的正交补空间。下面分别给出线性算子满足Weyl定理、Browder定理、(R)性质及(R1)性质的定义。
定义1[1]设T(H),若σ(T)σw(T)=π00(T),则称T满足Weyl定理,其中σ(T)为T的谱,σw(T)为算子T的Weyl谱,即
σw(T)={λ:T-λI不为Weyl算子},
并且
π00(T)={λisoσ(T):0 定义2[16]设T(H),若σ(T)σw(T)⊆π00(T),则称T满足Browder定理。 容易证明:T满足Browder定理当且仅当σw(T)=σb(T),其中 σb(T)={λ:T-λI不为Browder算子}。 令σab(T)与σa(T)分别表示算子T的Browder本质逼近点谱与逼近点谱,其中 σab(T)={λ:T-λI不为上半Fredholm算子或 asc(T-λI)=∞}, 且 σa(T)={λ:T-λI不为下有界算子}。 易证:λσab(T)当且仅当T-λI为半Fredholm算子且λ[isoσa(T)∪ρa(T)],其中ρa(T)=σa(T)。 定义3[13]设T(H),若σa(T)σab(T)=π00(T),则称T满足(R)性质,记作T(R)。 定义4[13]设T(H),若σa(T)σab(T)⊆π00(T),则称T满足(R1)性质,记作T(R1)。 首先,讨论线性算子同时满足(R1)性质与Browder定理的等价条件。为了方便表达,记 σc(T)={λ:R(T-λI)不闭}。 值得注意的是,尽管(R1)性质与Browder定理都是Weyl定理的变形,但两者并没有直接的关系,即(R1)性质成立并不能推断Browder定理成立;另外,Browder定理成立也不能推断(R1)性质成立。例如,对于全体2次可和的数列2: L(x1,x2,x3,…)=(0,x1,x2,…) 与后移算子 S(x1,x2,x3,…)=(x2,x3,x4,…) P(x1,x2,x3,…)=(0,x2,x3,…) 事实上,从上面的例子可以发现:Weyl定理与(R)性质之间也没有直接的关系。下面给出两者同时成立的等价条件。 定理1设T(H),则T(R1)且满足Browder定理当且仅当 σb(T)=[σw(T)∩{λ:n(T-λI)≥d(T-λI)}]∪ {λσ(T):n(T-λI)=0}∪σc(T)∪ [acc{λ:asc(T-λI)=∞}∩σw(T)]。 (1) 证明(充分性)由于 σb(T)=[σw(T)∩{λ:n(T-λI)≥d(T-λI)}]∪ {λσ(T):n(T-λI)=0}∪σc(T)∪ [acc{λ:asc(T-λI)=∞}∩σw(T)]⊆σw(T), 结合σw(T)⊆σb(T)无条件成立,于是σw(T)=σb(T),即T满足Browder定理。 对于(R1)性质,易证 [σa(T)σab(T)]∩[σw(T)∩{λ:n(T-λI)≥ d(T-λI)}]=∅。 另外, {σc(T)∪{λσ(T):n(T-λI)=0}∪ [acc{λ:asc(T-λI)=∞}∩σw(T)]}∩ [σa(T)σab(T)]=∅。 于是[σa(T)σab(T)]∩σb(T)=∅,即[σa(T)σab(T)]⊆[σ(T)σb(T)]⊆π00(T),因此T(R1)。 (必要性)只需要证明 σb(T)⊆[σw(T)∩{λ:n(T-λI)≥d(T-λI)}]∪ {λσ(T):n(T-λI)=0}∪σc(T)∪ [acc{λ:asc(T-λI)=∞}∩σw(T)]。 设 λ0[σw(T)∩{λ:n(T-λI)≥d(T-λI)}]∪ {λσ(T):n(T-λI)=0}∪σc(T)∪ [acc{λ:asc(T-λI)=∞}∩σw(T)]。 不妨设λ0σ(T),于是n(T-λ0I)>0且R(T-λ0I)为闭集。可以断言:λ0σw(T)。事实上,若λ0σw(T),则 λ0[{λ:n(T-λI)≥d(T-λI)}∪ acc{λ:asc(T-λI)=∞}], 从而n(T-λ0I) 由定义1至定义4可知:Browder定理与(R1)性质分别是Weyl定理与(R)性质的前提。因此,在定理1的基础上,下面研究有界线性算子同时满足(R)性质和Weyl定理的等价条件。 定理2设T(H),则T(R)且满足Weyl定理当且仅当 σb(T)=[σw(T)∩[acc{λ:asc(T-λI)=∞}]]∪ {λσ(T):n(T-λI)=0}∪{λ:n(T-λI)= ∞}∪[accσ(T)∩σc(T)]。 (2) 证明充分性。显见式(1)等号的右边包含式(2)等号的右边。另外,在定理1的证明中可知式(1)的右边总包含于σb(T)。因此,由定理1知T(R1)且T满足Browder定理。另一方面,由于 π00(T)∩{[σw(T)∩[acc{λ:asc(T-λI)=∞}]]∪ {λσ(T):n(T-λI)=0}∪{λ:n(T-λI)= ∞}∪[accσ(T)∩σc(T)]}=∅, 则π00(T)⊆[σ(T)σb(T)],于是π00(T)⊆[σ(T)σw(T)]且π00(T)⊆[σa(T)σab(T)]。综上可知T(R)且T满足Weyl定理。 必要性。只需证明 σb(T)⊆[σw(T)∩[acc{λ:asc(T-λI)=∞}]]∪ {λσ(T):n(T-λI)=0}∪{λ:n(T-λI)= ∞}∪[accσ(T)∩σc(T)]。 由于{λ:n(T-λI)=∞}⊆[σw(T)∩{λ:n(T-λI)≥T(T-λI)}]且 [σw(T)∩{λ:n(T-λI)≥d(T-λI)}]⊆[σw(T)∩ [acc{λ:asc(T-λI)=∞}]]∪σc(T)∪ {λ:n(T-λI)=∞}, 故由定理1可知, σb(T)⊆[σw(T)∩[acc{λ:asc(T-λI)=∞}]]∪ σc(T)∪{λσ(T):n(T-λI)=0}∪ {λ:n(T-λI)=∞}。 (3) 又由T满足Weyl定理知π00(T)=σ(T)σw(T)。于是 {λσ(T):n(T-λI)=0}∪{λ:n(T-λI)=∞}∪ accσ(T)=σb(T)。 (4) 对于任意不属于式(2)的右边的λ0,有 λ0[σw(T)∩[λ:acc{(T-λI)=∞}]]∪ σc(T)∪{λσ(T):n(T-λI)=0}∪ {λ:n(T-λI)=∞} 或者 λ0{λσ(T):n(T-λI)=0}∪{λ:n(T-λI)= ∞}∪accσ(T), 由式(3)和式(4)可知,不论是哪一种情况,总有λ0σb(T)。证毕。 设A(H),B(K),C(K,H),用MC(H⊕K)表示上三角算子矩阵 例1设L,S,P(2)定义为: L(x1,x2,x3,…)=(0,x1,x2,x3,…), S(x1,x2,x3,…)=(x2,x3,x4,…), P(x1,x2,x3,…)=(0,x2,x3,x4,…), (1)L(R1)且满足Browder定理; (2)B(R1)且满足Browder定理; (3)M0(R1)且不满足Browder定理。 解(1)σ(L)=σw(L)={λ:|λ|≤1},σa(L)=σab(L)={λ:|λ|=1},π00(L)=∅,即L(R)且满足Weyl定理,于是L(R1)且满足Browder定理。 (2)σ(B)=σa(B)={λ:|λ-1/2|≤1/4}∪{0},σw(B)=σab(B)={λ:|λ-1/2|≤1/4},π00(B)={0},即B(R)且满足Weyl定理,于是B(R1)且满足Browder定理。 (3)σ(M0)={λ:|λ|≤1},σw(M0)={λ:|λ|≤1}{λ:|λ-1/2|<1/4},σa(M0)={λ:|λ|=1}∪{λ:|λ-1/2|≤1/4}∪{0},σab(M0)={λ:|λ|=1}∪{λ:|λ-1/2|≤1/4},π00(M0)=∅,于是,M0(R1)且M0不满足Browder定理。 下面将刻画上三角算子矩阵同时满足Browder定理和(R1)性质,或者同时满足Weyl定理和(R)性质的条件。令T(H),用σSF-(T)、σSF+(T)分别表示T的下半Fredholm谱、上半Fredholm谱,其中 σSF-(T)={λ:T-λI不为下半Fredholm算子}, σSF+(T)={λ:T-λI不为上半Fredholm算子}。 定理3设A(H)和B(K),且σSF-(A)∩σSF+(B)没有内点。若σea(M0)=σw(M0),则对任意C(K,H),MC(R1)且满足Browder定理当且仅当M0(R1)且满足Browder定理。 证明当C=0时,显然必要性成立,因此,仅需要证明充分性成立。任给C(K,H),先证明MC满足Browder定理。设λ0σw(MC),则A-λ0I为上半Fredholm算子,B-λ0I为下半Fredholm算子。可以断言:d(A-λ0I)<∞且n(B-λ0I)<∞。若d(A-λ0I)=n(B-λ0I)=∞,则根据半Fredholm算子的摄动定理可知:存在ε>0,使得当|λ-λ0|<ε时,A-λI均为上半Fredholm算子,B-λI均为下半Fredholm算子且ind(A-λI)=ind(A-λ0I)=-∞,ind(B-λI)=ind(B-λ0I)=+∞。于是,当|λ-λ0|<ε时,有 d(A-λI)=d(A-λ0I)=n(B-λI)=n(B-λ0I)=∞。 由此可知λ0int[σSF-(A)∩σSF+(B)],这与σSF-(A)∩σSF+(B)无内点矛盾。因此,d(A-λ0I)<∞且n(B-λ0I)<∞。此时,A-λ0I与B-λ0I均为Fredholm算子且 ind(A-λ0I)+ind(B-λ0I)=ind(MC-λ0I)=0, 对于(R1)性质,设λ0σa(MC)σab(MC),则A-λ0I为上半Fredholm算子,n(A-λ0I)+n(B-λ0I)>0且asc(A-λ0I)<∞。因此,由半Fredholm算子的摄动定理可知:存在δ>0,使得0<|λ-λ0|<δ时,A-λI下有界且ind(A-λI)=ind(A-λ0I)。此时,若d(A-λ0I)=∞,则λ0intσSF-(A)。由于σSF-(A)∩σSF+(B)没有内点,因此,在λ0的任意小的空心邻域中总存在λ1,使得0<|λ1-λ0|<δ且B-λ1I为上半Fredholm算子。结合A-λ1I下有界可知:M0-λ1I为上半Fredholm算子且 ind(M0-λ1I)=ind(A-λ1I)+ind(B-λ1I)=-∞, 即λ1σea(M0)。又因为σea(M0)=σw(M0),所以M0-λ1I为Weyl算子,从而A-λ1I为Fredholm算子,这与ind(A-λ1I)=ind(A-λ0I)=-∞矛盾。综上可知d(A-λ0I)<∞,故A-λ0I为Fredholm算子。由文献[14]的定理2.2可知B-λ0I为上半Fredholm算子,且 ind(A-λ0I)+ind(B-λ0I)=ind(MC-λ0I)≤0。 于是M0-λ0I为上半Fredholm算子且 ind(M0-λ0I)=ind(A-λ0I)+ind(B-λ0I)≤0, 即λ0σea(M0)。由于σea(M0)=σw(M0),故M0-λ0I为Weyl算子。又因M0满足Browder定理,所以M0-λ0I为Browder算子,从而A-λ0I与B-λ0I均为Browder算子,故MC-λ0I为Browder算子,即λ0π00(MC)。综上可知:任给C(K,H),σa(MC)σab(MC)⊆π00(MC),即MC(R1)。证毕。 下面讨论上三角算子矩阵的(R)性质和Weyl定理同时成立的条件,首先给出1个引理: 引理1设A(H),B(K)。若n(A)<∞,dimR(A)⊥=∞,n(A)+n(B)>0且0isoσ(M0),则存在C(K,H),使得0π00(MC)。 证明若n(B)=0,则0 设eN(B)且满足‖e‖=1。令W=span{e},则dimW⊥=∞=dimR(A)⊥。由W⊥与R(A)⊥可分且维数相同知存在可逆等距算子T:W⊥→R(A)⊥。定义算子C(K,H)为: 注1在定理3中的条件下,若M0(R)且满足Weyl定理,并不能推出任给C(K,H),MC(R)且满足Weyl定理。 例2设S,E,F(2)分别定义为: S(x1,x2,x3,…)=(x2,x3,x4,…), E(x1,x2,x3,…)=(0,0,x2/2,0,x3/2,…), F(x1,x2,x3,…)=(0,0,x2/2,0,x4/2,…), 证明显然σSF-(G)∩σSF+(J)没有内点,且σea(M0)=σw(M0)。另外: (1)σa(M0)=σab(M0)={λ:|λ|≤1}∪{2},π00(M0)=∅,即M0(R); (2)σ(M0)=σw(M0)={λ:|λ|≤1}∪{2},π00(M0)=∅,即M0满足Weyl 定理。 下证:存在算子C(2),使得MC(R)且不满足Weyl定理。因为2isoσ(M0),n(G-2I)<∞,dimR(G-2I)⊥=∞,n(J-2I)>0,所以,由引理1知:存在C(2),使得2π00(MC)。但是,G-2I不为上半Fredholm算子,则2σ(MC)σw(MC)且2σa(MC)σab(MC),故对于C,有MC(R)且不满足Weyl定理。证毕。 下面在“M0(R)且满足Weyl定理”的条件下,给出使得“对任意C(K,H),MC(R)且满足Weyl定理”成立的条件。 定理4给定算子A(H),B(K),设σSF-(A)∩σSF+(B)没有内点且σea(M0)=σw(M0),若 (1)M0(R)且满足Weyl定理; (2)G={λisoσ(M0):n(A-λI)<∞,d(A-λI)= ∞,n(A-λI)+n(B-λI)>0}=∅, 则任给C(K,H),MC(R)且满足Weyl定理。 证明由定理3的证明可知,只需要证明对任意的C(H),有π00(MC)⊆σ(MC)σb(MC)。设λ0π00(MC),则0 若n(B-λ0I)=0,则0 若n(B-λ0I)>0,则由条件(2)可知d(A-λ0I)<∞,即A-λ0I为Fredholm算子。断言:n(B-λ0I)<∞。事实上,若n(B-λ0I)=∞,则可考虑以下2种情况: 综上可知n(B-λ0I)<∞,于是λ0π00(M0)。又因M0满足Weyl定理,因此M0-λ0I为Browder算子,从而A-λ0I和B-λ0I均为Browder算子,故MC-λ0I为Browder 算子,即λ0σ(MC)σb(MC)。证毕。 注2在定理4中,条件“σea(M0)=σw(M0)”是本质的。 例3设A,S(2)分别定义为: A(x1,x2,x3,…)=(0,0,x1,x2,…), S(x1,x2,x3,…)=(x2,x3,x4,…), 证明显然σSF-(A)∩σSF+(S)无内点,且定理4中的(1)和(2)成立。但是,σea(M0)={λ:|λ|=1},σw(M0)={λ:|λ|≤1},因此σea(M0)≠σw(M0)。 下证:存在C(2),使得MC(R1)。设为2的一组正规正交基,其中en为第n个坐标为1、其他均为0的向量。令U=span{e1,e2},则dimU=2=d(A)=dimR(A)⊥,因此,存在等距可逆算子T:U→R(A)⊥。定义C:2→2为:2 Weyl定理与(R)性质的判定

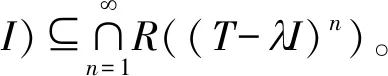

3 上三角算子矩阵的(R)性质和Weyl定理