江苏省常州市宋剑湖高级中学(213011) 蔡立艳

山东省邹平双语学校(256200) 姜坤崇

我们知道,实轴和虚轴等长的双曲线叫做等轴双曲线,它的两条渐近线互相垂直,其离心率为.等轴双曲线是特殊的双曲线,它除了具备一般双曲线的所有性质外,还具有一些特殊的性质,本文给出笔者探寻的等轴双曲线的若干有趣性质(这些性质是非等轴双曲线所不具有的),以飨读者.

性质1设F1、F2是等轴双曲线Γ :x2−y2=a2(a> 0)的两个焦点,O是Γ 的中心,P是Γ 上的任意一点,则|PF1|、|OP|、|PF2|成等比数列.

证法1如图1,设F1(−c,0),, 当点P不在Γ实轴的端点时, 在∆PF1O、∆POF2中分别使用余弦定理得

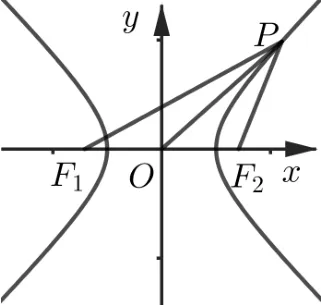
图1

性质2设P是等轴双曲线Γ:x2−y2=a2(a>0)上的任意一点,l1、l2是过Γ 中心O且关于Γ 的一条渐近线对称的两条定直线,则P到l1、l2的距离的平方差为一定值.

证明如图2, Γ 的两条渐近线方程为y=±x. 设P(x0,y0),则由点P在Γ 上知. 不妨设l1、l2是关于直线L:y=x对称的两条定直线,当l1、l2不为两条坐标轴时,设其方程分别为kx−y= 0、x−ky= 0(k为常数,且k̸1),则P到l1、l2的距离d1、d2的平方分别为

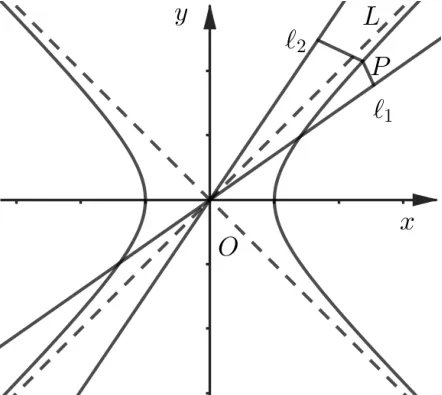
图2

当l1、l2为两条坐标轴时,由等轴双曲线的方程知结论显然成立.

性质3给定等轴双曲线Γ :x2−y2=a2(a> 0),l1、l2是过Γ 中心O且关于Γ 的一条渐近线对称的两条定直线,A、B分别是l1、l2上的一点,且AB中点P在Γ 上,则|OA|2−|OB|2为一定值.

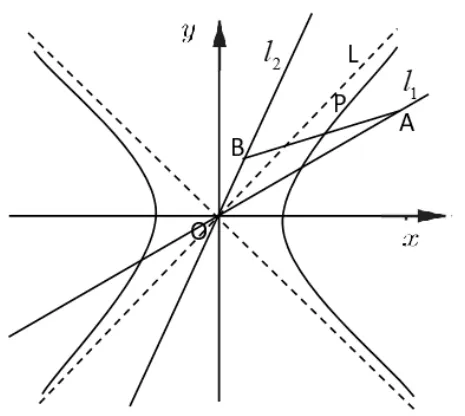
图3

性质4设P是等轴双曲线Γ:x2−y2=a2(a>0)上异于顶点的任意一点,A(−a,0),B(a,0)是Γ 的两个顶点,PA、PB与y轴的交点分别为C、D,则|PA|·|PC|=|PB|·|PD|.

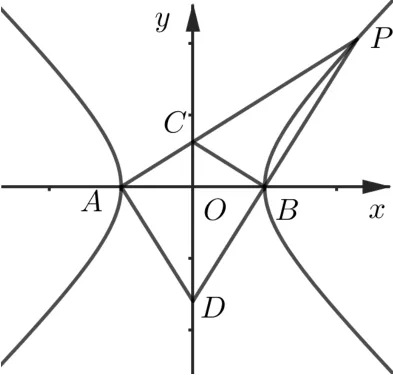
图4

性质5给定等轴双曲线Γ:x2−y2=a2(a>0),F是它的一个焦点,过F引互相垂直的两条弦AB、CD,且AB的两端点都在F对应的Γ 的同一支上,CD的两个端点分别在Γ 的两支上,则|AB|=|CD|.

性质6给定等轴双曲线Γ:x2−y2=a2(a>0),其中心为O,左、右顶点分别为A1、A2,F是Γ 的右焦点,过F作垂直于x轴的直线交Γ 在第一象限于点P,直线A1P与Γ的渐近线在第一象限的交点为M,设kA2M、kA2P分别为直线A2M、A2P的斜率,则

(1)∆OA2M为等腰三角形;

(2)kA2M+kA2P=0;

(3)∆PMA2为等腰直角三角形.

图5

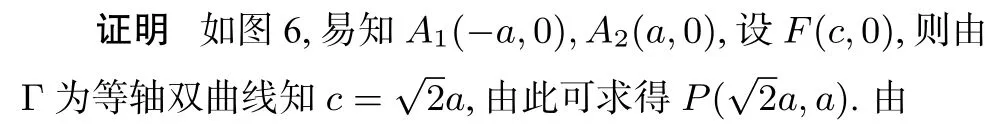
图6

性质7设AB是等轴双曲线Γ 过中心O的任意一条弦,P是Γ 上异于A、B的任意一点,直线PA、PB分别交两条渐近线于点C、E;D、F,则|PC|=|PD|,|PE|=|PF|.

证法1设等轴双曲线的方程为Γ:x2−y2=a2(a>0),由Γ 是等轴双曲线知两条渐近线方程为y=±x,其斜率分别为1、−1. 如图7,不妨设C、D在渐近线l1:y=x上,则E、F在渐近线l2:y= −x上. 设P(x,y),则x2−y2=a2.又设直线AB的方程为y=kx(|k| < 1),则与Γ 的方程联立解得

图7

同理可证|PE|=|PF|.

证法2如图8,以Γ 的两条渐近线为坐标轴建立直角坐标系,不妨设C、D在x轴上,则E、F在y轴上,设Γ 的方程为xy=m(m>0),P(x,y),则xy=m. 又设直线AB的方程为y=kx(k>0),则

若设直线PA、PB的斜率分别为kPA、kPB,则

即kPA= −kPB, 由此得∠PCD= ∠PDC, ∠PEF=∠PFE, 即∆PCD和∆PEF均为等腰三角形, 从而|PC|=|PD|,|PE|=|PF|.

说明对于性质7 中的等轴双曲线问题, 一般是通过建立坐标系使其方程为x2−y2=a2(a> 0)(如证法1)来解决,但这样做对于此问题不但要使用直线的到角公式,而且整个解题过程的运算量较大. 而以上证法2 另辟蹊径,以两条渐近线为坐标轴建立直角坐标系(其双曲线的方程为xy=m(m> 0))来进行,则不仅方法新颖巧妙而且其证明过程相对于证法1 大为化简.