苏 雅

(扬州大学数学科学学院,江苏 扬州 225100)

1 “化动为静”——动边转移求解范围问题

例1(2021年徐州市中考第28题)如图1,正方形ABCD的边长为4,点P在边AD上(点P不与点A,D重合),连接PB,PC,将线段PB绕点P顺时针旋转90°得到PE,将线段PC绕点P逆时针旋转90°得到PF.连接EP,EA,FD.

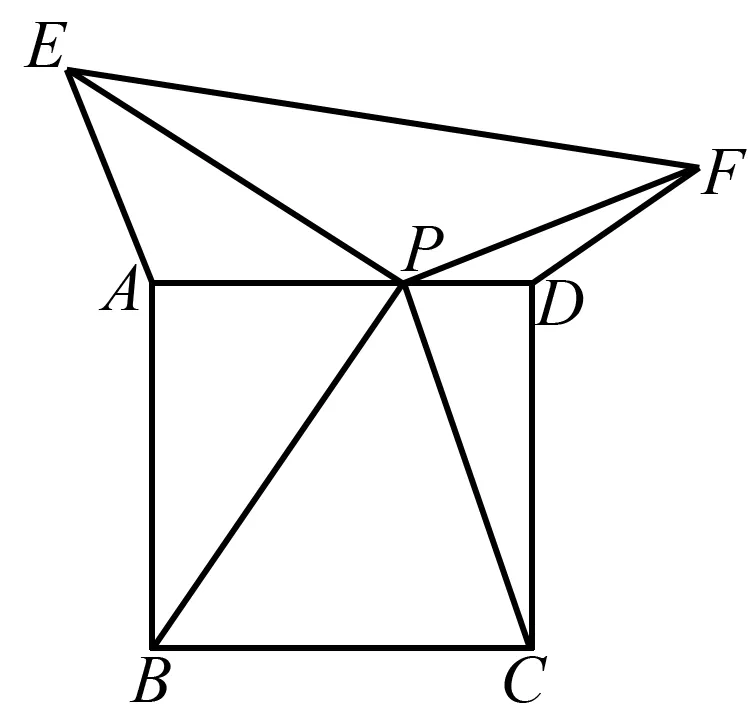
图1

(2)如图2,EA,FD的延长线交于点M,取EF中点N,连接MN,求MN的取值范围.

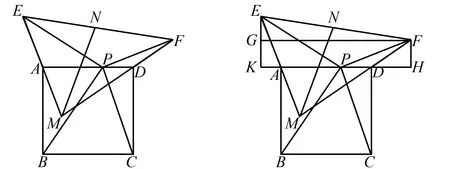
图2 图3

解(1)①如图3,过F作FH⊥PD交PD的延长线于点H.

易证△PCD≅△FPH,

②同理,过E作EK⊥PA交PA的延长线于点K,则△PKE≅△BAP,

易证AK=PD=FH,KE=AP=DH,

易得AE=DF.

(2)如图3,过F作FG⊥KE,易证四边形FHKG为矩形,

∴GF=KH=8,GK=FH.

设AK=PD=FH=KG=x,

∴KE=AP=4-x,

GE=KE-KG=(4-x)-x=4-2x.

在Rt△EGF中

∵△AKE≅△FHD,

∴∠EAK=∠DFH,

又∵∠DFH+∠FDH=90°,

易证∠MAD+∠ADM=90°,

∴∠EMF=90°,

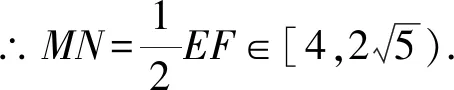
评析此类题目要学会从题干中找信息,将需要求证的结果作为目标,去寻找与之相关的参数,前两问都是要证明边与边的关系,应将不易求证关系的边进行转移,并利用边的关系构造或寻找全等三角形进行求解;第三问,常见的求动线段范围的方法有:将动线段的一端点转移使之变成定点,另一端点转移到固定直线上,即变成了点到直线的距离.也可将其整体转移至一个新的直角三角形中,利用勾股定理和代数求解.本题中出现了中点,可联想到中位线或直角三角形斜边,将所求动线段进行整体转移,再构造直角三角形,利用代数求解.

变式1如图4,边长为6的正方形ABCD中,E为BC的中点,F为正方形内一点且EF=2,连接DF,以DF为边在右侧作正方形DFGH,则EH的最小值为( ).

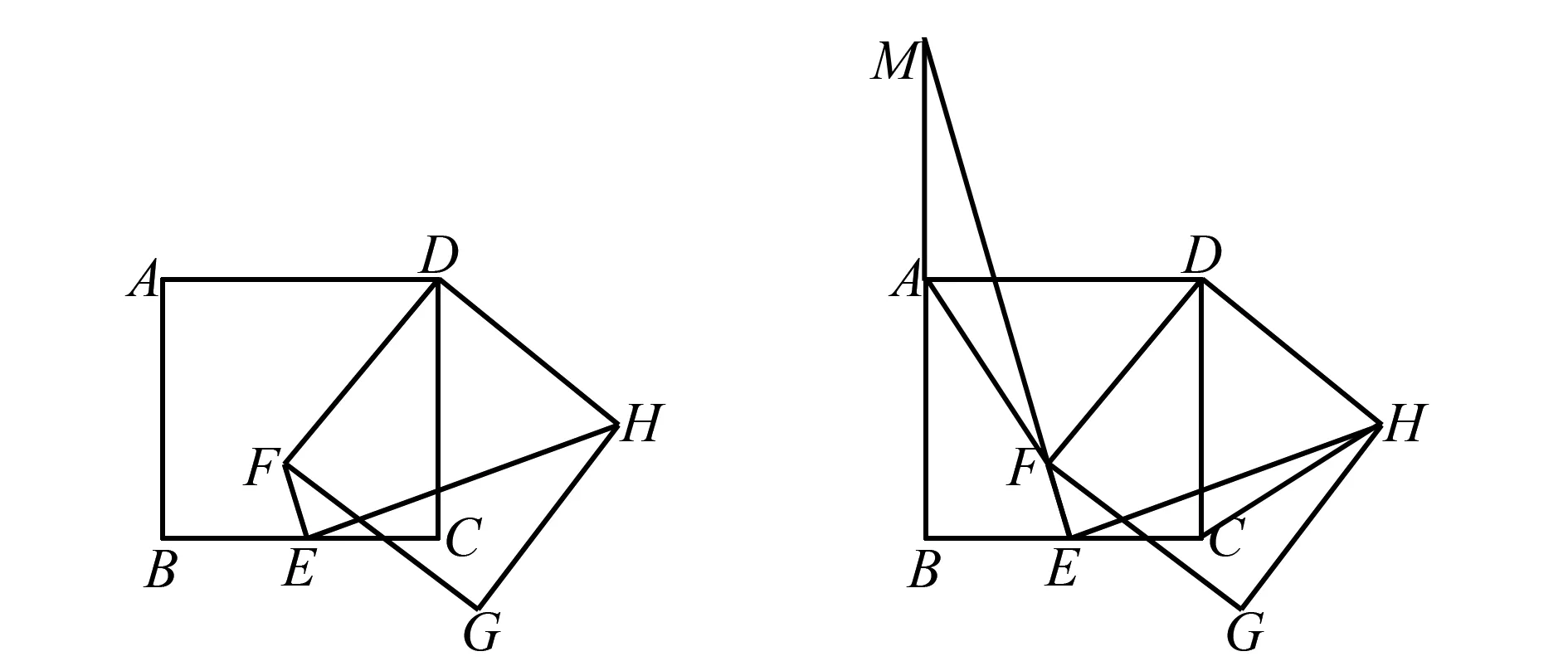
图4 图5

解如图5,连接CH、AF,延长BA使MA=EC,连接MF,易证△ADF≅△CDH(SAS),

∴AF=CH,∠DAF=∠DCH.

易证△MAF≅△ECH(SAS),

∴FM=EH.

当M、E、F三点共线时,EH最小,

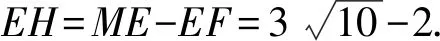
评析求动线段最小值问题归属于范围问题.看到中点,尝试将动线段利用中位线或直角三角形斜边定理进行转移,此题这两种方法都无法做到,该题目中出现了两个正方形,且有一共同顶点,此时必有全等出现,可以联想到利用全等将所求动线段进行转移,出现了“隐藏”△EFM,可利用三角形三边关系进行求解.

2 “以静制动”——从特殊点剖析动点轨迹,求路径问题

例2(2021年连云港市中考第27题)在数学兴趣小组活动中,小亮进行数学探究活动.

(1)△ABC是边长为3的等边三角形,E是边AC上的一点,且AE=1,小亮以BE为边作等边三角形BEF,如图6所示,求CF的长.

图6

(2)△ABC是边长为3的等边三角形,E是边AC上的一个动点,小亮以BE为边作等边三角形BEF,如图6所示,在点E从点C到点A的运动过程中,求点F所经过的路径长.

(3)△ABC是边长为3的等边三角形,M是高CD上的一个动点,小亮以BM为边作等边三角形BMN,如图7所示,在点M从点C到点D的运动过程中,求点N所经过的路径长.

图7 图8

(4)正方形ABCD的边长为3,E是边CB上的一个动点,在点E从点C到点B的运动过程中,小亮以B点为顶点做正方形BFGH,其中点F、G都在直线AE上,如图8所示.当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为____,点G所经过的路径长为____.

解(1)易证△ABE≅△CBF(SAS),

∴CF=AE=1.

(2)易证△ABE≅△CBF(SAS),

∴CF=AE,∠BCF=∠A=60°,

∴∠FCE=120°,

∴∠FCE+∠A=180°,∴CF∥AB,

∴点E在点C处时,CF=AC,点E与点A重合时,点F与点C重合.∴F的运动路径为AC=3.

(3)如图9,取CB中点,连接HN.

易证△MDB≅△NHB(SAS),

∴∠NHB=∠MDB=90°,

点M在点D处时,点N与点H重合,

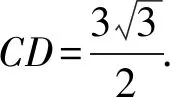
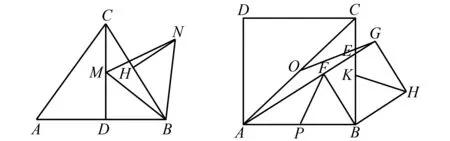
图9 图10

(4)如图10,取AB中点P,BC中点K,连接FP,HK,易证△BHK≅△BFP(SAS),

∴H的轨迹为一段圆弧,

点E在点B处时,点F、G、H与点B重合,

点E在点C处时,∠FBE=45°,KH⊥BC,

易证△ABF≅△CBH(SAS),

∴∠BHC=∠AFB=90°,从而C、G、H共线,

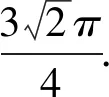
评析当出现两个有共同顶点的同类多边形(一般为三角形或四边形)时,一定有全等出现,如果没有,可以构造全等三角形.路径长度,就是要找到所求点运动的全过程所对应的线段长.该题中前两问都是简单的单一直线运动,只需要找到所求点的初始与终止位置,求出对应的线段长度,即为路径长度.第三问点的运动稍微复杂,当所求点位置不好确定时,可以构造与所求点相关的线段,来判断其运动轨迹,发现所求点的运动轨迹均为单一方向的圆弧,找到其初始位置与终止位置即可求解.

3 反思总结,提高学生解题能力

对于动点问题,学生首先要能够明辨题目中的变量和不变量.只有分清楚变量和不变量才能够化动为静,将所求的变量转化到恒定的不变量上.具体问题中通常是将运动的点或边,转移到不变的边上,这样问题也就迎刃而解了.其次,动点在运动过程中的特殊点,也是解题的突破口之一,要抓住关键点,将一般情况特殊化,观察运动过程,进而能够发现动点的运动规律.对于与函数有关的动点问题,要尝试建立动点运动过程中的函数关系,利用函数性质进行求解.

只要掌握了动点问题的解题策略,不论动点怎么动,我们都能以不变应万变,顺利求解此类试题.动点问题常常较为综合,求解过程也要运用多种数学知识,所以能有效地考查学生的数学知识和数学能力,有效区分不同考生的数学学习水平,为中学阶段的选拔提供一定依据.

教师在教学中要注意培养学生的几何素养,有意训练学生的动态思维,将动点问题中的“动”与条件中的“静”结合起来,学会运用数形结合等数学思想方法,再结合专项训练,一定可以提高学生对动点问题的求解能力.