卢凤婷

（太原师范学院 山西晋中 030619）

数与代数部分是中学数学教学的四大板块之一，是学生认知数量关系、探索数学规律、构建数学模型的基础，能够让学生从数的角度清晰认识、理解和表达世界。数与代数领域的学习，有助于学生形成抽象能力、推理能力和模型观念，发展几何直观和运算能力[1]。

数与代数部分同样也是中考数学的重要组成部分，主要涵盖了数与式、方程与不等式和函数三个板块，是学生在初中数学学习中必须掌握的重点知识，在中考数学中占据了一半的分值。数学思想作为数学解题的重要思想，在解决数与代数问题时有重要的作用。

一、函数思想在中考数学数与代数部分解题中的应用

对于中学数学，函数思想的应用主要体现在：首先是能够借助初等函数的性质来解决相关含参问题；其次是在解决问题的过程中，建立函数关系式，把钻研的问题转变为与函数相关的问题，以实现化繁为简，化难为易[2]。在具体的解题过程中，面对很多实际问题，我们无法利用相同领域内的知识完成问题的分析和解决，这时需要我们将其转化为函数问题，从而完成求解[3]。

例1如图1，平面直角坐标系中，正四边形OABC的顶点O落在坐标原点，边长为2，A点，C点分别位于x轴和y轴的正半轴上。函数y=2x的图象与CB交于点D，函数（k为常数，k≠0）的图象经过点D，与AB相交于点E，与函数y=2x的图象在第三象限内交于点F，连接AF、EF。求函数的表达式，并写出E点和F点的坐标。

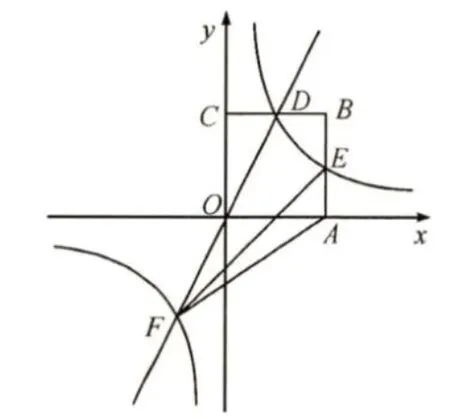
图1

问题分析：该题目是山西省2017年中考题第18题。解决这一题目的关键就是要利用函数思想，将几何问题转化为函数问题进行求解。在解题中，可以借助待定系数法完成求解。首先根据题目条件，我们可以知道正方形OABC且边长为2，点A，点C分别在x轴，y轴的正半轴上，所以A点的坐标是（2，0），C点坐标是（0，2）；函数y=2x的图象与CB交于点D，CB的解析式为y=2，所以两个方程构建二元一次方程组，联立求解得到交点D的坐标（1，2）；函数（k为常数，k≠0）的图象经过点D，所以点D函数上，点D的坐标满足该函数的解析式，利用待定系数法，就可以求得函数的表达式。E的坐标可以根据点A坐标和数的表达式求得，F的坐标是点D关于原点的对称点，可根据点D坐标求得。这一题目主要考查学生数学思维的灵活转化能力，从题型上看，本题主要是正方形和反比例函数的交点问题，单纯通过反比例函数的相关知识去解决这一问题难度较大，如果通过构建函数的方式分析问题，借助函数思想和待定系数法就能够将这一复杂的问题简单化，提高学生的解题效率。

二、转化思想在中考数学数与代数部分解题中的应用

转化思想就是指从不同的角度思考，另辟蹊径地将新知识与旧知识联系到一起。在初中数学学习中，转化思想是学生解决数学习题的有效途径。学生灵活应用转化思想，解决某些难以入手的证明题、计算题，能提高学习信心[4]。

例2，如图2，正方形ABCD内接于⊙O，⊙O的半径为2，以点A为圆心，以AC为半径画弧交AB的延长线于点E，交AD的延长线于点F，则图中阴影部分的面积是（）。

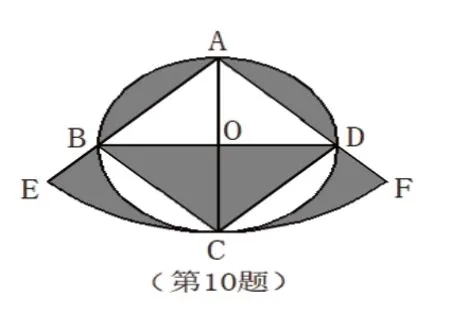
图2

A.4π-4 B.4π-8 C.8π-4 D.8π-8

问题分析：该题目是山西省2018年中考题选择题最后一题，从这道题的位置来看，处于选择题压轴题的位置，学生一开始可能会产生畏难情绪。但是仔细看这道题，我们发现阴影部分的面积可以转化，利用在转化思想，我们可以把不易解决的问题转化成已解决的问题或者易解决的问题。图中阴影部分的面积是分散的，我们利用拼补的方法可以把上半圆的阴影补到下半圆的空白地方，阴影部分的面积就完整了，求分散的阴影部分的面积我们就可以转化成求一个整体的阴影面积。而转化后的整体面积就是大扇形面积减去一个三角形的面积，大扇形的面积和三角形的面积都是学生易解决的问题，这道题就迎刃而解了。所以在日常教学中加强学生的联想思考，让学生在面对难题时能迅速找到解题的切入点，采用补形转化、换元转化、化繁为简、问题变更等方法，完成习题的解析与论证。

三、数形结合思想在中考数学数与代数部分解题中的应用

数形结合是将数学之中的“数”与“形”相结合，将复杂的问题简单化，将抽象的问题直观化，利用图形的直接性和数据的严谨性更好地解决问题[5]。数学教师在讲课过程中应有意识地利用数形结合思想解决问题，让学生多养成数形结合的思维，更好地解决数学问题。

例3：已知点A,（x1，y1），B（x2，y2）,C（x3，y3）都在反比例函数（k＜0）的图象上，且x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（ ）。

A.y2＞y1＞y3B.y3＞y2＞y1C.y1＞y2＞y3D.y3＞y1＞y2

问题分析：该题目是山西省2020年中考题选择题第7题。对于这一问题，如果单纯地通过函数和取值范围的角度去思考，很难找到解题的突破口，尤其是对于反比例函数这类极为抽象的知识点。借助数形结合思想，能够完美解决。在解题的过程中，可以将函数转化为图形，根据反比例函数中k的正负，判定函数图像的走势，这样就将原来的函数问题转化为反比例函数的图像问题，最后将关键点的坐标代入就可以完成求解。当k＜0时，函数图像就是从左往右逐渐上升的，y值会随着x值的增大不断增大。此时，整个问题就会变得思路清晰，解题难度就会降低。

四、分类讨论思想在中考数学数与代数部分解题中的应用

分类讨论思想是一种最基础的解决困难的思维战略，旨在将所要研究的对象按照标准分为若干不同的类别，在挨个研究的进程中，实现分而治之。分类讨论思想贯穿初中数学教学，包括概念、定理、公式、运算性质、不确定的量等，它同样也是培养学生良好数学思维品质的关键方法。分类讨论思想也是中考数学解题中一种重要的解题思想，该思想主要应用于函数部分问题中，尤其是对于二次函数，a取值的不同直接影响着整个解题思路。在解题的过程中，要注重对二次项系数的正负和常数项的正负做好分类讨论，根据不同的情况判断函数曲线。

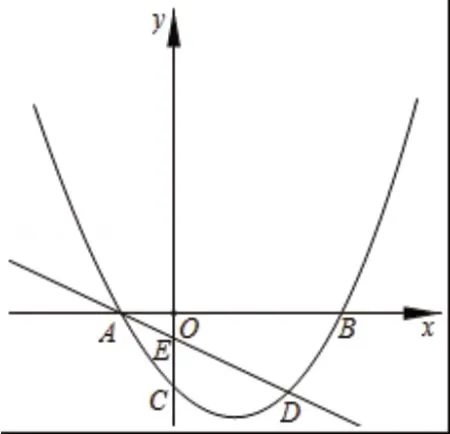
图3

问题分析：该题目是山西省2020年中考第23题1，2小问。在求解这一问题的时候，解析问题（1）只需要学生将函数所对应的方程值为0时就可求得与x轴的交点A，B两点的坐标，再联合点D和点A的坐标，求得直线l的函数表达式。但是，对于问题（2）动点问题，则需要学生考虑实际情况，进行分类讨论，在此过程中，教师应该起到引领的作用，启发学生运用该思想进行探索：

PM与直线l交于点N当点N是线段PM的三等分点，而点N是线段PM的三等分点，可以是靠近P的三等分点，也可以是靠近M的三等分点。所以可分两种情况进行讨论：

第一种是|MN|=2|PN|，第二种是2|MN|=|PN|，M、N、P三点的坐标均可以用含m的代数式表达，所以根据不同的等量关系可以列出等式，即可解出满足关系的m，得到点P的坐标。在动点问题中，应用分类讨论思想，使得学生在解析问题的时候，能够全面分析影响因素，做到高效解题。分类讨论思想的运用可以提高学生的思维能力，又可以使学生形成良好的解题习惯。

五、方程思想在中考数学数与代数部分解题中的应用

方程思想作为中学数学中主要的思想之一，它主要是立足于具体数学问题，在正确理解的基础上，将问题中文字语言转变为相应的数学语言，并建立起相关的数学关系——方程或方程组，然后通过解方程（组），从而解决问题，习得一种新型的思维方式.通俗而言，方程思想就是“实际问题→数学问题→代数问题→方程问题”这样一个过程。

例5：2020年5月，太原举行了“活力太原·乐购晋阳”消费暖心活动，此次活动中的电器消费券单笔消费满600元立减128元（一次只能使用一张）。某品牌电饭煲以进价的150%进行标价，假如按标价的80%售卖，一位客人购置该电饭煲时，使用一张电器消费券后，又付了568元。请问该电饭煲的进价是多少。

问题分析：该题目是山西省2020年中考第17题。这道题是生活中常见的销售问题，依据是商场售价=买家应付款这一等量关系，由于题目中已知标价为销售价的15%，且八折销售，买家在付款时有满600减128的优惠，买家在优惠后付款568，所以买家应付款为568+128。因此可设进价为x，根据这一等量关系，x·（1+50%）·0.8=568+128，解得x=580。类似的实际问题可以让学生熟悉生活常见模型，将未知数表示出来后代入等量关系中。列方程解应用题的学习能让学生直观感受和应用方程思想，明白未知量与已知量之间的等量关系。

六、建模思想在中考数学数与代数部分解题中的应用

在新课标理念下，中学数学的教学慢慢向教学生如何解决现实问题进行转变。对于学生来说，解决繁杂的实际问题还是有一定的挑战，而数学建模可以帮助学生将烦琐的现实问题抽象为易懂的数学问题，用数学知识去求解，这样能够大幅度地提高了学生的解题的速度，而且培养学生解决问题的能力。

例6：图4是某车站的一组智能通道闸机，当行人通过时智能闸机会自动识别行人身份，识别成功后，两侧的圆弧翼闸会收回到两侧闸机箱内，这时行人即可通过。图5是两圆弧翼展开时的截面图，扇形ABC和DEF是闸机的“圆弧翼”，两圆弧翼成轴对称，BC和EF均垂直于地面，扇形的圆心角∠ABC=∠DEF=28°，半径BA=ED=60cm，点A与点D在同一水平线上，且它们之间的距离为10cm.求闸机通道的宽度，即BC与EF之间的距离（参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）；

图4

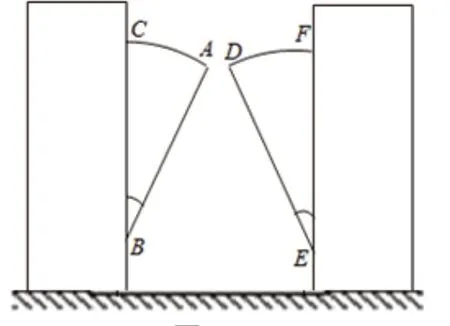
图5

问题分析：该题目是山西省2020年中考第21题第1小问。这道题把实际生活中遇到的闸机问题抽象成了两圆弧翼展开时的截面图，构建了一个数学模型，从而帮助解题。题目中给了扇形圆心角的大小，给了半径的长度，我们可以分别过C，D点作BC和EF的垂线从而构造直角三角形，以此达到解题的目的。通过构建几何模型并转变为三角函数问题来解，将现实问题转化为几何问题，从而解决问题。与实际模型比较，在初中数学中根据建模思想建立各种数学模型还处于初级阶段。数学教学中应该把学习知识、应用知识、探索发现和建模求解更好地联系在一起，使学生灵活应用数学建模思想，学会用数学的思维思考。

我们由以上的例子可以看到，数学思想方法是处理数学问题的指导思想和基本策略，是形成学生数学能力、数学意识的桥梁，是数学的灵魂。所以，在学习数学的过程中，学生需要不断对方法和思想进行总结渗透，使它上升至一个高度，形成数学思想方法，并用数学思想方法指导我们解题，这样才能运用数学和驾驭数学，成为学习数学的真正主人。