钱浩浩，金浩铭，刘韩彬，章丽娜

(湖州师范学院 理学院，浙江 湖州 313000)

0 引 言

近30年来，具有peakon解的非线性波方程引起了众多学者的关注.Peakon解最早是由Camassa和Holm[1]提出的，之后学者们陆续得到了其他peakon方程，如Degasperis-Procesi方程[2-3]、完全非线性K(m,n)方程[4-5]和Novikov方程[6-7]等，这些方程都是具有peakon解的可积模型.Peakon解因在波峰处具有不连续的一阶导数而被称为单峰孤立尖波解.

本文主要研究双分量Dullin-Gottwald-Holm(DGH)方程：

(1)

其中，m=u-α2uxx.当ρ=0时，方程(1)是Dullin-Gottwald-Holm方程；当γ=0时，方程(1)是双分量Camassa-Holm方程.文献[8]研究指出，双分量Camassa-Holm方程只有光滑的孤立波解.为研究线性色散项uxxx对孤立波解的光滑性影响，文献[9]研究了双分量DGH方程(1)在无穷边界条件下的各种光滑孤立波解和非光滑孤立波解的渐进行为,但没有给出方程(1)peakon解的精确表达式.

本文利用动力系统分支方法[4,10]，研究双分量DGH方程(1)peakon解的动力学行为及其精确表达式，并通过分析行波系统在不同参数条件下的相图，获得一类新的非光滑孤立波解——拟扭波解的精确表达式.

为研究方程(1)的行波解，令u(x,t)=u(ξ),ρ(x,t)=ρ(ξ),ξ=x-ct,其中c为波速，则方程(1)的第二个方程可化为：

-cρ+(uρ)′=0.

(2)

对方程(2)进行积分，得:

(3)

其中,g为积分常数.方程(1)的第一个方程为：

-c(u-u″)′-Au′+γu‴+(u(u-u″))′+(u-u″)u′+ρρ′=0.

(4)

对方程(4)进行积分，并令积分常数为零，得：

(5)

方程(5)等价于二维系统：

(6)

系统(6)的首次积分为：

(7)

系统(6)第二个方程的右端在直线u=c和u=c-γ上是不连续的，这意味着双分量DGH方程(1)很有可能存在非光滑行波解.

1 系统(6)的正则系统的相图分支

为讨论简便，设A=0,c>0.下面考虑系统(6)的正则系统：

(8)

其中，dξ=2(u-c)2(u-c-γ)dτ.系统(6)和系统(8)具有相同的首次积分，因此系统(6)和系统(8)具有相同的拓扑相图.u=c和u=c+γ是系统(8)的两条不变直线解.根据几何奇异摄动理论，在这两条直线附近，τ是快变量，ξ是慢变量，即在奇异直线u=c和u=c+γ附近，系统(6)和系统(8)具有截然不同的动力学性质.

为分析系统(8)的平衡点，记

f(u)=u(3u-2c)(u-c)2+g2，

f′(u)=2(u-c)(6u2-6cu+c2)，

f″(u)=2(18u2-24cu+7c2).

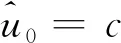
设M(uj,yj)为系统(8)在平衡点Ej(uj,yj)处线性化系统的系数矩阵，记J(uj,yj)=detM(uj,yj)，则

J(u1,2,0)=-2(u1,2-c)2(u1,2-c-γ)f′(u1,2)，

根据平面动力系统基本理论，对于平面可积系统的一个平衡点，当J<0时，该平衡点是鞍点；当J>0时，该平衡点是中心；当J=0且平衡点处的Poincare指数为零时，该平衡点是尖点.

记hi=H(ui,0),i=1,2,hs=H(c+γ,∓Ys)，利用上述信息进行定性分析，得到系统(8)的相图分支，见图1.

图1 系统(8)在(u,y)平面上的相图分支

2 Peakon解和拟扭波解的参数表达式

下面讨论双分量DGH方程 (1) 的peakon解和拟扭波解的精确表达式.由方程(7)，对任一固定的积分常数h，有

(9)

根据系统(6)的第一个方程，对首次积分H(u,y)=h所定义的水平曲线进行积分，得：

(10)

其中，u(ξ0)=u0.一般而言，方程(10)的右端是一个超椭圆积分，故不易积分，但在某些特殊情况下，可以积分求得peakon解和拟扭波解的精确参数表达式.

2.1 Peakon解

下面讨论如图1(b)和图1(d)所示的两种情况.

(i)当h2=hs时，存在一个异宿轨道环连接系统(8)的3个鞍点，即E2(u2,0)，S+(c+γ,Ys) ，S-(c+γ,-Ys)，且环绕着中心E1(u1,0)(图1(b)).此时，

G(u)=(u-u2)2(c+r-u)(uL-u).

因此，沿曲线E2S+和S-E2积分，并结合式(10)可得：

于是，方程(1)peakon解的参数表达式为 (图2(a))：

图2 波形图

(11)

其中，

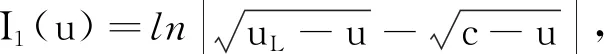
(ii)对应连接系统(8)的3个鞍点，即E1(u1,0)，S+(c+γ,Ys)，S-(c+γ,-Ys)，且环绕中心E2(u2,0)的三角形异宿轨道环H(u,y)=h1=hs(图1(d))，有

G(u)=(u-u1)2(c+γ-u)(uL-u).

沿曲线E2S+和S-E2积分，并结合(10)可得：

于是，方程(1)peakon解的参数表达式为 (图2(b))：

(12)

其中，

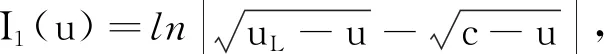
2.2 拟扭波解

当u2

(13)

其中，

G(u)=(u-u2)2(uM-u)(uL-u),c+γ

将式(13)代入系统(6)的第一个方程，并沿着上述两条双曲扇形曲线积分，得到两个拟扭波解的精确表达式 (图2的(c) (d))：

(14)

其中，F(φ,k)和∏(φ,α2,k)是勒让德椭圆积分，且

3 结 论

本文运用动力系统方法研究了双分量DGH方程的非光滑行波解及其动力学行为，获得了两个新的peakon解的参数表达式，并得到了新的拟扭波解的参数表达式.通过分析可知，peakon解取决于一个曲线三角形的存在 (图1(b)和图1(d))，具有确定的几何性质.