贾大卫， 吴子燕， 何 乡

(西北工业大学 力学与土木建筑学院, 西安 710129)

随着经济和城市的发展，人们的生活与建筑结构等基础设施系统的关系越来越密切。地震具有较强的突发性和破坏性，会给人类生命和建筑功能带来巨大威胁。由于地震激励具有较强的不确定性，结构的抗震性能通常采用概率评估方法。美国太平洋地震工程研究中心(Pacific Earthquake Engineering Research Center，PEER)对此进行了大量研究，率先提出新一代 “基于性能的地震工程”(performance based earthquake engineering, PBEE)概率决策框架，近几年第二代PBEE理论也逐渐完善[1]。该理论的基础为概率地震需求分析，主要用来计算在具体场地下结构在设计年限内超过给定性能极限状态的结构需求年平均超越概率。地震需求是场地危险性与结构地震易损性相结合的产物，其含义是对所有地震风险事态作用下所对应的结构需求概率的积分。

国内外学者开展了大量有关概率地震需求分析的研究，并取得了丰硕的成果。钟剑等[2]基于全概率理论进行了桥梁结构的地震风险分析；Jiang等[3]考虑了不同的场地特征对地铁站地震易损性的影响；Khorami等[4]计算了钢框架结构的易损性和地震危险性曲线；Banihashemi等[5]考虑了结构的整体性能，进行了钢框架的地震易损性和可靠性分析；蒋亦庞等[6]考虑结构参数的不确定性，建立了无筋砌体结构的地震易损性曲线，并探讨了结构参数的不确定性对结构性能的影响；Khaloo等[7]采用桥墩柱的最大弯曲延性响应建立了桥梁结构的易损性曲线，并且考虑了时变损伤效应。Jafarian等[8]基于多种地震强度参数建立了多参数易损性函数。但上述研究存在一些不足：其一，部分研究仅基于一维工程需求参数(engineering demand parameter，EDP)进行分析，而未考虑多种EDP的联合作用。结构在地震激励下破坏形式比较复杂，仅考虑一种参数难以得到准确的评估结果。其二，在传统概率地震需求分析中，普遍采用基于对数正态分布假定的理论分析法，即将结构EDP视为服从对数正态分布的概率随机变量。该假定使用方便，但却具有一定局限性。Mangalathu等[9]通过Kolmogorov-Smirnov 非参数检验法，验证了桥梁结构的EDP拒绝服从对数正态分布；Cornell等[10]认为桥梁各构件的易损性曲线并非全部满足对数正态分布假定；Karamlou等[11]认为对数正态分布假定会引起结构易损性分析结果的不准确；袁万城等[12]认为部分EDP和地震强度之间不满足对数线性回归的假设。上述研究表明，对数正态分布假定并不完全适用于任意结构，可能会导致分析结果产生较大误差。其三，决大多数研究人员采用固定阈值作为结构性能极限状态划分的标志。例如Wang等[13]采用固定阈值分别定义了桥墩柱和支座的性能极限状态；Zhang等[14]和Su等[15]同样采用固定阈值定义了结构的性能极限状态。已有研究表明[16]，不同地震波作用下结构性能极限状态阈值会产生显著差异，忽略阈值的随机性会引起较大偏差。张鹏辉等[17]基于变异系数[17]衡量阈值的随机性，但变异系数的选择大多根据专家经验或已有研究主观确定，缺少理论依据。

本文在多维性能极限状态下，提出基于高斯混合模型(Gaussian mixture model ,GMM)[18]的概率地震需求分析法。该方法不需要假定EDP和阈值的分布类型，并且可以充分考虑阈值的随机性。首先基于多维性能极限状态方程衡量结构在地震激励下的损伤程度，然后不采用对数正态分布假定，利用GMM分别拟合EDP和阈值的概率密度函数，建立概率地震需求分析的多重积分公式，最后利用MC模拟得到结构需求的年平均超越概率。将本文所提方法与传统方法进行对比，突出其差异性。

1 高斯混合模型

GMM是单高斯概率密度函数的延伸。它采用有限个高斯分布的概率密度函数的线性加权组合来拟合任意形状的概率密度分布。基于GMM的概率密度函数可以表示为

(1)

对一个M元的GMM，未知参数共有3M组，每一元高斯分布的参数为：v={πk,μk,δk} 。可通过期望最大化(expectation maximization,EM)算法进行迭代估计。该算法主要思想是通过最大化目标函数的一个下限函数来间接地最大化目标函数。假设有N组观测数据，迭代格式如式(2)～式(5)所示

(2)

(3)

(4)

(5)

(6)

在GMM中，首先需要确定高斯分布的个数才能利用EM求解未知参数。可预先随机取高斯分布个数，利用贝叶斯信息准则(Bayesian information criterion,BIC)或赤池信息准则(Akaike information criterion，AIC)判断最优GMM。BIC值越大或AIC值越小说明概率密度函数拟合效果越好。

2 概率地震需求分析

2.1 基本原理

概率地震需求分析包含结构易损性和地震危险性分析两部分内容，其意义在于：既采用概率方法计算结构在不同强度地震下的破坏概率，又考虑场地危险性，将二者耦合得到年平均超越概率，如式(7)所示

(7)

式中：F为结构年平均超越概率；R为EDP；r为阈值。P(R>r|IM)为某地震强度下EDP超过给定性能极限状态阈值的概率，即地震易损性；fIM(im)为地震强度的概率密度函数。文献[19]表明，地震易损性表示为概率地震需求模型在失效域的积分，即

(8)

式中，f(R|IM)为给定地震强度下结构的概率地震需求模型，即EDP的概率密度函数。

我国目前建筑结构抗震设防的依据为抗震设防烈度，有资料表明，采用极值Ⅲ型分布描述地震烈度的概率分布比较符合我国的实际情况[20]，分布函数如式(9)所示

(9)

式中:w为地震烈度的上限值，可取为12；ε为众值烈度，表示年平均超越概率为0.632的地震烈度；K为形状参数，一般采用最小二乘法确定。

将式(8)～式(9)代入式(7)，即可得到概率地震需求分析的计算公式，如式(10)所示

(10)

2.2 基于多维性能极限状态的概率地震需求分析

多维性能极限状态描述多种EDP联合作用下结构的极限状态[21]，可通过多维性能极限状态方程描述，如式(11)所示

(11)

式中：NEDP为EDP个数；Ri为EDP；ri为EDP在对应性能极限状态下的阈值；bi为系数，也被称为相互作用因子，决定了极限状态曲面的形状。当L<0时认为结构发生破坏，黄小宁等[22]指出，在两种EDP的条件下，可将一个EDP的b简化为1，如式(12)所示

L=1-(R1/r1)b-(R2/r2)

(12)

以两种EDP为例，在多维性能极限状态下，易损性表示为EDP的概率密度函数在失效域内的积分，如式(13)所示

P=∬L<0f(R1,R2|IM)dR1dR2

(13)

式中：IM为给定的地震强度；f(R1,R2|IM)为EDP的联合概率密度函数。

已有研究表明，在多维性能极限状态下，地震需求一般通过如下三重积分公式表示

(14)

3 基于GMM和阈值随机性的地震需求分析

与基于一维EDP的地震需求分析相比，式(14)可以考虑不同EDP作用下结构的联合性能极限状态，更符合实际。但在式(14)中，结构易损性的积分域是由多维性能极限状态方程确定。而极限状态方程中的随机变量仅包含EDP，因此无法考虑极限状态阈值的随机性。Liu等[23]提出了基于离散阈值的积分方法考虑阈值的随机性，但该方法需要假定阈值的分布类型，并求解数次乃至数十次三重积分，计算代价较大。

由式(13)可知，多维性能极限状态下易损性分析的本质，是在给定EDP概率密度函数的条件下计算性能极限状态方程小于0的概率。因此本文将阈值同样视为概率随机变量从而考虑其随机性。仍以二维EDP为例，本文暂不考虑阈值和EDP相关性，假定阈值的联合概率密度函数为f(r1,r2)，将其代入式(13)，结构易损性可以表示为

(15)

式(15)的积分域同样由性能极限状态方程确定。但与式(13)相比，在式(15)中取阈值为随机变量，由二重积分拓展到四重积分，因此可以充分考虑阈值的随机性。联立式(14)和式(15)，多维性能极限状态下基于阈值随机性的地震需求可以表示为

(16)

本文所提方法的核心思想是通过GMM拟合(R1,R2|IM)和f(r1,r2)，而并非传统对数正态分布假定。由于引入了GMM，式(16)的积分十分复杂，很难得到解析解。因此引入蒙特卡洛(Monte Carlo ,MC)模拟提高计算效率。谷音等指出，若地震强度的分布函数已知，可通过抽样将地震危险性函数进行离散。假定抽取的地震强度样本个数为nim，则每个样本出现的概率为1/nim。谷音等提出了结构需求年均超越概率的MC法，如式(17)所示

(17)

式中：IM=imi为抽样所得单个地震强度样本；P(R>r|IM=imi)反映了在该地震强度样本下结构的破坏概率。但式(17)只考虑了一维EDP，并不适用于多个EDP的情况，因此本文将式(17)推广到多维性能极限状态下的概率地震需求计算。将式(17)代入式(16)，可得

(18)

采用Wang等建议的MC法求解四重积分，分别对基于GMM构造的f(R1R2|IM)和f(r1,r2)进行抽样，获得样本(R1j,R2j,r1j,r2j)，则结构易损性表示为

(19)

式中：nEDP为生成的样本点总数；I(·)为指示函数，当L(R1j,R2j,r1j,r2j)<0时I(·)=1，反之为0。将式(19)代入式(18)，有结构需求年平均超越概率

(20)

式(20)即为本文最终建立的基于GMM的概率地震需求分析公式。由于GMM所得概率密度函数形式比较复杂，本文采用舍选抽样法[24]获得f(R1,R2|IM)和f(r1,r2)样本。算法流程如图1所示。

图1中：[a,b]为随机变量的取值区间；M为概率密度函数在区间内的极大值。

与传统概率地震需求分析方法相比，本文所提方法优势在于：f(R1,R2|IM)和f(r1,r2)由GMM确定，不需要对EDP和阈值进行对数正态分布假定，也不需要人为选取阈值的变异系数，还可以充分考虑阈值的随机性。基于GMM的概率地震需求分析流程，如图2所示。

4 算例分析

4.1 结构模型建立

本文基于SAP2000分别建立一个钢筋混凝土(reinforced concrete,RC)框架-剪力墙结构和一个RC框架结构，结构模型如图3和图4所示。其中框剪结构沿X方向共5跨，跨度均为8 m；沿Y方向共3跨，边跨跨度6 m，中跨跨度8 m。沿Y方向主梁间设置单根次梁。该结构共4层，各层层高均为3.6 m。抗侧力体系由混凝土框架和剪力墙部分组成。剪力墙部分包括两片单肢剪力墙及由两个电梯井组成的核心筒，核心筒长8 m，宽4 m，门洞高2.4 m，宽2 m。各构件采用的混凝土强度等级均为C30，纵向受力钢筋采用HRB400级，箍筋采用HRB335级。楼板和剪力墙均配置双排HRB335级钢筋。框架结构沿X方向共5跨，跨度为4 m；沿Y方向共3跨，跨度为5 m。结构总共8层，各层层高均为3.6 m，构件的材料属性与框剪结构一致。

梁和柱均采用SAP2000中的Frame单元模拟，并在梁两端布置P-M3铰，柱两端布置P-M2-M3铰用于考虑其非线性行为，铰采用SAP2000中默认的铰属性。剪力墙采用分层壳单元[25]，在三个应力分量上均考虑其非线性行为。混凝土楼板采用Membrane单元。此外，模型考虑了P-Δ效应。本文采用的混凝土和钢筋的本构关系如图5所示。

文献[26]指出，最大层间位移角(maximum inter-story drift ratio，MIDR)能较好地反映结构构件的整体损伤大小。文献[27-28]指出，在考虑非结构构件的损伤时，主要考虑对加速度敏感的构件，例如机械设备、内部管道等，因而本文选择MIDR和最大层加速度(peak floor acceleration,PFA)分别作为衡量结构和非结构构件性能的EDP。

4.2 场地危险性分析

拟定两个结构模型所处的场地土类别为I，抗震设防烈度为7度，设计基本地震动加速度为0.1 gal，场地特征周期为0.35 s，结构的阻尼比取0.05，周期折减系数为0.9，设计基准周期为50年。50年超越概率为0.632，众值烈度约为5.45度。则有：

(21)

通过最小二乘法可得形状参数K的值约为8.318 9，则地震烈度的分布函数为

(22)

在地震工程学中，峰值地面加速度(peak ground acceleration，PGA)是衡量地震强度的关键指标之一。本文选择PGA衡量地震强度的大小，因此需要将地震烈度换算为PGA，采用谷音等给出的换算公式，如式(23)所示

PGA=10(im·lg-0.01)

(23)

将式(23)代入式(22)，并将PGA的单位用gal表示，可得PGA的累积分布函数为

(24)

分别对式(22)和式(24)两端求导，可得地震烈度和PGA的概率密度函数曲线。由于PGA累计分布函数形式比较复杂，在MC模拟中，首先根据式(22)生成nim个地震烈度样本，然后将这些样本根据式(23)转化为PGA样本。本文取nim=100 000，抽得的地震烈度和转化后的PGA样本分布及其概率密度函数曲线如图6和图7所示。由图可知，生成的PGA样本与概率密度函数拟合度较高，这些样本能在考虑场地类型的前提下较全面地反映设计年限内地震强度的随机性。

4.3 地震激励不确定性

文献[29]表明，在概率地震需求分析中，需要选择多于20条地震波进行非线性时程分析。根据场地特征参数，基于SAP2000提取目标反应谱，从PEER数据库中选择了25条震级6～7级、震中距15～20 km、剪切波速200～300 m/s的地震波，并基于文献[30]合成了25条地震波。所得地震波的反应谱如图8所示。

4.4 基于增量动力分析法的EDP计算和阈值确定

增量动力分析(incremental dynamic analysis，IDA)法是地震需求分析中常用方法之一。它的基本思想是将地震波按一系列的地震强度进行调幅，然后基于非线性时程分析得到不同地震强度下结构的EDP，通过样条插值得到EDP-IM曲线，即IDA曲线。IDA法的最大优势在于，不仅可以获得不同强度地震下EDP的值，还可以根据IDA曲线斜率判断在不同性能极限状态下的阈值。FEMA中规定，在IDA曲线中，坐标轴原点和第一个EDP-IM点之间的线段斜率为K，曲线斜率出现较大变化的点定义为“立即使用”；当曲线斜率小于0.2K时，该点定义为“防止倒塌”；当曲线趋于平缓时定义为“整体失稳”。在GB 50011—2010《建筑抗震设计规范[31]中，性能极限状态分为“正常使用”、“轻微破坏”、“中等破坏”和“严重破坏”四个等级。“正常使用”对应于弹性状态阈值，“轻微破坏”的阈值约为“中等破坏”的50%，“严重破坏”约为弹塑性阈值的90%。根据IDA曲线斜率，本文定义性能极限状态分为“正常使用(NU)”、“中度损伤(MD)”、“严重损伤(SD)”和“发生倒塌(CO)”四个等级。NU定义为曲线斜率开始变化的点，对应于FEMA中的“立即使用”点；MD定义为曲线斜率小于0.5K的点；SD定义为曲线斜率小于0.2K的点，对应于FEMA中的“防止倒塌”点；CO定义为曲线斜率小于0.04K的点，对应于FEMA中的“整体失稳”点。本文采用PGA衡量地震强度，将每条地震波的PGA分别调幅至0.1～1.0 gal，步长增量取0.1 gal。本文将每条地震波的输入方向均设置为双向加载，加载方式为1·X+1·Y。这里给出框剪结构的IDA曲线及定义的阈值，如图9所示。

通过统计分析，四种性能极限状态下MIDR阈值的变异系数依次为0.229 0，0.272 1，0.411 6，0.498 7，PFA依次为0.163 5，0.234 6，0.473 9，0.543 7。随着破坏程度的提高，变异系数也随之变大。该现象表明：阈值随机性会对分析结果产生不可忽视的影响；在不同性能极限状态下采用相同的变异系数是不合理的。

4.5 基于GMM的EDP和阈值概率密度函数建立

正如第1章和第3章所述，本文通过GMM得到f(R1,R2|IM)和f(r1.r2)，而并非传统对数正态分布假定。利用IDA法得到的数据，分别在不同PGA和不同性能极限状下建立EDP和阈值的概率密度函数。以框剪结构在PGA=0.1 gal和NU性能极限状态为例，如图10所示。

4.6 地震需求分析

根据式(12)建立性能极限状态方程，如式(25)所示

L=1-(MIDR/midr)b-(PFA/pfa)

(25)

在二维极限状态方程中，本文将PFA对应的b取为1。由于缺少框剪结构的统计数据，初步拟定MIDR的b=1，后文将通过灵敏度分析讨论b的值对超越概率的影响。基于4.5节建立的GMM生成f(R1,R2|IM)和f(r1,r2)样本，分别在不同性能极限状态下利用式(20)得到结构需求年平均超越概率。为对比GMM法和传统方法的差异，同样基于对数正态分布假定进行求解。Wang等和Liu等已经分别给出了基于对数正态分布假定的易损性和概率地震需求分析的详细说明，本文不再重复，结果如表1所示。

表1中λp=(Fgmm-Flog)/Flog·100%，Fgmm和Flog分别为基于GMM和对数正态分布假定的年均超越概率。λp反映了二者的相对差异。由表1可知， 在四种性能极限状态下λp均为负，说明基于GMM得到的年均超越概率均小于对数正态分布假定的年均超越概率，这个结论对RC框架和框剪结构均成立。同时，在NU下，两个结构λp的绝对值均大于15%，在MD和SD下λp的绝对值大于30%，而在CO下大于50%。该结果表明GMM得到的年均超越概率与传统方法相比差异很大。由于GMM不需要人为假定参数分布类型，因此对数正态分布假定会导致较大误差。

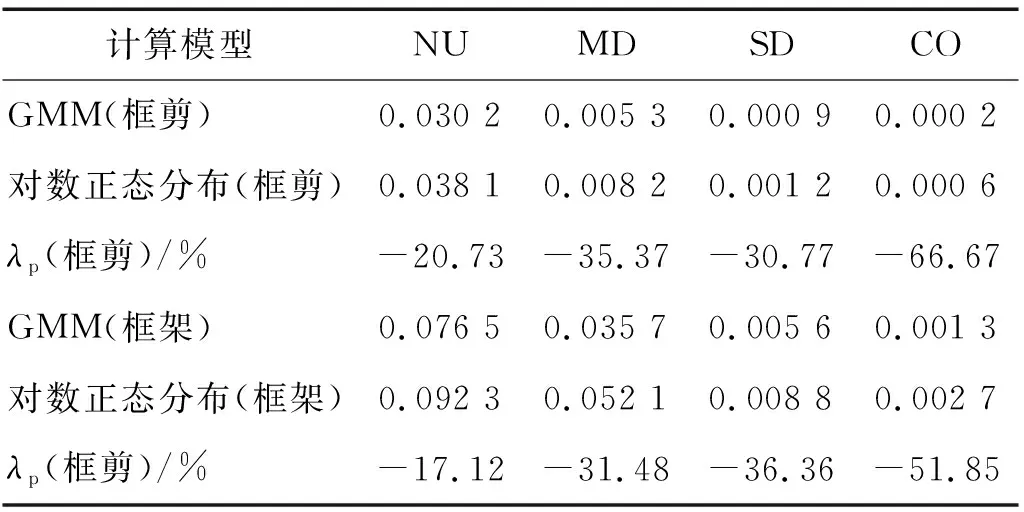
表1 年均超越概率

为更加直观的表示GMM对年平均超越概率的影响，本文将年平均超越概率用危险性曲面表示。危险性曲面反映了当EDP取不同值时的结构需求在设计年限内的年平均超越概率，如图11所示。由图11可知，基于GMM得到的危险性曲面低于传统对数正态分布假定，说明基于GMM法所得年平均超越概率较小，而基于对数正态分布假定得到的年平均超越概率较大。因此对数正态分布假定可能会低估结构的抗震性能。

4.7 参数灵敏度分析

相互作用因子b会影响到性能极限状态方程的非线性程度，改变失效域的大小。Wang等和刘骁骁等[32]对b与结构失效概率的关系在对数正态分布假定下进行了大量研究。随着b增大，结构需求年平均超越概率逐渐降低。本文利用刘骁骁等采用的灵敏度分析法，探究基于GMM的危险性曲面与b的关系。在4.6节基础上，分别再取b=2,b=5,b=10,b=15，所得危险性曲面如图12所示。

比较不同b对应的危险性曲面可知，随着b增大，危险性曲面逐渐下移，年平均超越概率逐渐降低。与b=10相比，当b=15时，危险性曲面有所下降，但二者基本重合。这个结论对GMM和对数正态分布假定均成立，均适用于RC框架和框剪结构，且与Wang等所得结论一致。Wang等的研究表明，b的值反映了不同EDP性能极限状态的相关性，b越大，相关性越弱，当EDP统计参数相同时，所得失效概率越小。因此在基于多维性能极限状态的地震需求分析中，忽略性能极限状态的相关性不利于结构安全。

5 结 论

本文考虑性能极限状态阈值的随机性，并且不对EDP和阈值的分布类型进行人为假定，提出基于GMM的概率地震需求分析法。基于IDA法确定不同PGA下EDP的值，基于IDA曲线斜率获得阈值样本，利用GMM拟合EDP和阈值的概率密度函数取代传统对数正态分布假定，建立了考虑阈值随机性的概率地震需求分析的多重积分公式，通过MC法求解年均超越概率。所得结论如下：

(1)通过IDA法可知，阈值具有较强的随机性，并且随机性会随破坏程度的提高而增加。一方面，忽略阈值的随机性会导致分析结论的不准确；另一方面在不同性能极限状态下采用相同的变异系数描述阈值的随机性是不合理的。

(2)与传统基于多维对数正态分布假定的概率地震需求分析相比，基于GMM得到的结构需求年平均超越概率偏小。该结论表明对数正态分布假定可能会低估结构的抗震性能，得到不准确的评估结果。

(3)在二维性能极限状态方程中，b越大，EDP性能极限状态相关性越弱，当采用相同的EDP和阈值概率密度函数后，所得年平均超越概率越小。因此忽略性能极限状态的相关性会导致地震需求概率偏低，不利于工程安全。

(4) 本文建立的分析模型为RC框剪和RC框架结构，因此所得结论仅适用于该类型的结构模型，对其它类型的工程结构，GMM和阈值随机性对年平均超越概率的影响仍需建立模型具体分析。