基于数值解的非线性振动系统定性分析
2022-10-27张红兵李万祥
陈 宁, 张红兵, 李万祥
(兰州交通大学 机电工程学院,兰州 730070)
在非线性振动系统的定性研究中,庞加莱映射是极其重要的思想工具,可以将连续微分动力学系统转化离散差分动力学系统,使之深化对分叉行为和过程的研究。在非线性动力学研究中,定量分析是定性分析的基础,定量分析的结果是定性分析中庞加莱映射得以构建的基础。但是在当前的研究中,对复杂的、难以解析或不可解析的振动系统,定性研究的深度远不及对其的定量分析。这是由于对这类系统无法得到精确的解析解,而在现行的定性分析方法中,一个可以被分析的庞加莱映射必须依赖精确的解析解,而非数值解。
非线性振动系统的定量分析方法可划分为解析法和数值法两个范畴,与之相对应的在定性分析过程中,理论上也具有依靠解析解和数值解两种构建庞加莱映射的基本方式。为便于下文阐述,将映射的可视化结果简称映像,将映射的迭代不动点简称为平衡点,分别将通过精确解析解、近似解析解和数值解构架起来的庞加莱映射简称为解析映射、近似解析映射和数值映射。
庞加莱映射只是一个特殊的运算,从本质上来说依靠精确的解都可以构建起系统的庞加莱映射。Luo等[1-3]考虑了分段线性系统可以分段解析的特点,利用解析解以及周期运动的假设构建系统的周期映射,深刻地揭示了含间隙振动系统的分叉过程和机理。其中得出擦边可能是导致分叉奇异的发现和结论,这既是非线性动力学领域持续关注的热点之一[4-6],也是机械振动系统中普遍需要解决的问题之一。但是大多数的系统都不能利用解析法进行定量分析,如文献[7-9]中针对含库伦摩擦振动系统做出的研究,虽然可以分段解析,但是系统中由于间隙和摩擦力的两个相互不干涉的因素存在,无法完全以解析的方法构建系统的庞加莱映射,必须采用分支程序以辅助完成对系统分叉的分析。类似这种结合解析解和数值方法的定量分析方法可以统称为半解析法,是针对复杂分段线性系统切实有效的方法,如李万祥等[10]就单自由度非光滑系统采用半解析法进行研究,得出单自由度碰撞振动系统也可以存在Hopf分叉的发现。
面对更加复杂的系统,如分段光滑系统中,是难以分段精确解析的,陈洪月等[11]在对采煤机这类复杂设备的动力学响应研究中,就只能以数值模拟的方法求得系统的庞加莱截面图。可以说,基于精确的解析解、半解析解和数值解都是可以构建起系统的庞加莱映射。
对于解析映射可以方便地利用不动点处雅可比矩阵的特征值信息,对系统中发生的分叉等做出精确的判别,如文献[12]中对内伊马克沙克-音叉分岔点处的两参数开折问题的研究。但是对于数值映射,由于缺少后续对应的分析方法,对其研究只能止步于观察数值映像的分叉图和结合经验做出分析,然后利用经验对系统中的分叉行为等做出解释,如文献[13]中关于采煤机和复杂齿轮系统的动力学特性研究,就以数值模拟的方法结合庞加莱截面法求得系统的数值映像及分叉图,但是并未做到文献[14]中对分叉分析的深刻成度,仅依靠观察分岔图从而得出部分规律。上述现象反映出数值映射的可分析性不足,不像解析映射那样可以对庞加莱映射平衡点做出分析,这也是数值映射不被广大学者所公认的原因。
数值求解适合于所有振动系统的求解,这是解析分析所不具备的优势。虽然数值映射的概念尚未被认可,但是已有大部分学者在变相地使用,如文献[15-19]中针对含摩擦系统、分段光滑系统、含间隙系统等复杂多体动力学系统的研究,通过大量庞加莱截面法来分析问题,其过程的本质是庞加莱映射的数值化实现方法,其结果和解析映射的结果一样为庞加莱映像图。
数值计算的适用性更强,应用面更广,但是数值映射在定性研究中发挥的作用却相对更小,这其中也包含学者对数值解精确性有所怀疑的因素。大量的理论分析和试验证明,只要严格控制算法稳定性,必定可以保证系统的积分精度。鉴于其求解精度,数值解是目前大多数近似解析方法精度验证的标准。如刘汝逾等[20-22]在解决非线性振动问题时,就以数值解为标准对各自所提出的近似解析法的求解精度进行验证。大量拓展近似解析法的论文,都以数值解验证近似解析解精度,这说明数值解具有比近似解析解更高的可靠性。
针对数值映射尚不能被分析研究的问题,部分学者尝试采用近似解析解替代精确解析解建立系统的近似解析映射,但是目前还没有实质性的突破以便在实际中广泛应用。虽然一个成熟的近似解析方法足以对系统做出有效的定量研究,但是函数映射的特点和近似解析解的本质特征也决定利用近似解析映射可能导致定性分析结果失真的必然性。
因此,考虑数值映射的可靠性和广泛的适用性,如果能够对数值映射找到与之匹配的分析过程和方法,必定可以深化对不可解析甚至难以解析振动系统的定性分析。
分叉点处庞加莱映射迭代不动点的雅可比矩阵特征值是研究高余维分叉的关键,目前成熟的方法中缺乏对数值映射迭代不动点极其雅可比矩阵特征值的求解方法,这是导致对复杂系统定性分析深入度不足的主要原因,也将是本课题研究的主要工作。
1 近似迭代不动点的数值计算方法
系统庞加莱映射的迭代不动点是分叉行为分析的关键,因此利用数值映射的本质特点寻找分叉点附近系统的迭代不动点是首要工作。
1.1 关于分叉点处庞加莱映射的分析
在系统分叉点的某个去心邻域内无论迭代过程是渐近收敛还是发散状态,其在时间进程中向稳定状态过渡的过程都十分缓慢。由于这种过程的缓慢性和稳定性,通过自然迭代的方法求解不动点是不现实的,但是也为和其他方法的结合提供可能性和前提条件。
在此定义某种基于数值解建立的离散动力系统,由映射Py描述,如式(1)所示。
ynyn+1=Py(μ,yn)yn
(1)
式中:yn+1为系统参数yn在映射Py作用下的象; 映射Py由原像yn和参数μ共同决定。
设映射Py的迭代不动点为Y,根据不动点的映射条件应该满足如式(2)所示的代数方程,则Y同样的和参数μ相关。
Y=Py(μ,Y)Y
(2)
参数yn可以表示为关于不动点Y和不动点的误差εn之间的关系,如式(3)所示。将式(3)代入式(1),并将Py(μ,yn)按Taylor级数在不动点Y处展开,代入式(2)可以重构与映射Py等价的映射Pε如式(4)所示, 映射Pε可以描述误差参数εn和εn+1之间的映射关系,如式(5)所示。
yn=Y+εn
(3)
(4)
εnεn+1=Pε(μ,εn)εn
(5)
式中:εn为参数yn相对于不动点Y的误差; 原点O即映射Pε的不动点,满足式(6)所示的平衡关系。
O=Pε(μ,O)O
(6)
当系统的不动点稳定时,映射Pε在原点O处的谱半径ρ[Pε(μ,O)]<1。假设系统在参数μ=μ0处发生某种基于不动点的经典分叉,此时必然有ρ[Pε(μ0,O)]=1,即存在Pε的雅可比矩阵的特征值λ满足如式(7)所示的形式,和分叉参数μ0有关。
λj(μ0)=cosθ±sinθi∈diag[Pε(μ0,O)]
(7)
利用映射关系式(5)分析扰动εn的传递情况
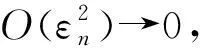
(8)
假设存在转化矩阵Qε(μ0,O)使Pε(μ0,O)可以对角化为Λε(μ0,O),满足式(9)的形式。
Qε(μ0,O)εn+1=Λε(μ0,O)Qε(μ0,O)εn
(9)
令Qε(μ0,O)εn=Zn,则映射Λε可以表示误差εn正则化后的误差参数Zn和Zn+1之间的映射关系,如式(10)所示。
Zn+1=Λε(μ0,O)Zn
(10)
当条件式(7)成立时,初始扰动εn在某个空间方向或者空间曲面内临界稳定,既不会收敛,也不会发散,保持相对初值的稳定性,则式(10)在迭代过程中必然满足式(11)的关系。
‖Zn+1‖=‖Zn‖
(11)
但是在一般情况下,由于计算的精度以及其他原因,只能够确定分叉参数所在的某个邻域,即仅仅可以找到某个μ∈U(μ0),可以表示为
μ=μ0+μΔ
(12)
则特征值式(7)可表示为含有误差的形式
λj(μ)=[cos(θ+θΔ)±sin(θ+θΔ)i][1+Δλ]∈
diag[Pε(μ,εn)]
(13)
式中: Δλ为由于参数μ的误差引起的谱半径的变化,Δλ=ρ[Pε(μ,εn)]-1;θΔ为特征值辐角的误差; 此时若有μΔ→0, 则Δλ→0,(1+Δλ)→1,且使条件式(14)成立。
‖Zn+m-Zn‖=
‖Zn‖[1+Δλ]m-‖Zn‖≪‖Zn‖
(14)
说明在有限次数的迭代之后,由于系统的发散和收敛造成的摄动的变化量要远远小于初始摄动量。在系统的某个维度面上,如系统的正则范式所对应的基平面,状态参数的某些分量绕特定的点发生旋转,此时其平衡点近似在旋转中心位置所在,但是由于其衰减指数十分接近1,故而其旋转半径的摄动量十分小。利用映射关系式(5)可知即便是收敛情况,通过持续迭代求取迭代不动点也是极其困难的,当迭代发散时,必然是一种不可取的方案。
1.2 算法原理和过程
在自然迭代过程中,如果初始状态的摄动量‖Zn‖变化速度较为缓慢,则在有限的时间内,‖Zn‖的值会保持相对的稳定,可以借助这种相对稳定特征来加速迭代收敛的过程。
在此,可以借助分叉点处映射的特征进行迭代不动点的求解,如图1所示。图1中:O为其理论平衡点在系统特定低维度子空间中的投影;Zn,Zn+1,Zn+2为连续相邻三次状态构成的庞加莱映像,近似满足式(15)、式(16)的关系;Oμ为其外接圆心。
(15)
∠ZnOZn+1=∠Zn+1OZn+2=θ+θΔ
(16)
可设庞加莱映像中状态参数的坐标如式(17)所示。
Zn[‖εn‖cos 0,‖εn‖sin 0],
Zn+1[‖εn+1‖cos(θ+θΔ),‖εn+1‖sin(θ+θΔ)],
Zn+2[‖εn+2‖cos(2θ+2θΔ),
‖εn+2‖sin(2θ+2θΔ)]
(17)
利用几何关系可求得外接圆圆心Oμ坐标
(18)
计算的外接圆心的理论摄动半径和初始状态摄动半径之比如式(19)所示。
(19)
当sinθ→0时,代入式(19)可得
(20)
由式(20)可以看出,当|sinθ|>|Δλ|时,经过该方法计算后的摄动量是绝对小于自然迭代过程的,对平衡点失稳的状态同样适用。初始状态Zn经过两次自然迭代后的摄动半径为‖Zn+2‖=‖Zn‖(1+Δλ)2,和自然迭代法相比,其收敛速度之比如式(21)所示。
(21)
当sinθ=0时,
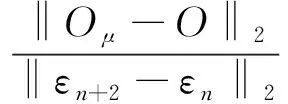
(22)
同样满足当|sinθ|>|Δλ|时,该迭代计算过程是绝对收敛的,且效率绝对优越于自然迭代。
1.3 算法稳定分析和修正
式(22)也反映出对于sinθ=0的情况该算法效果不太理想,极有可能导致算法失稳失效。对于这种情况,可以给出算法失效的判决方式和替代计算方法。
在此以运算前的初始状态和运算后的初始状态,分别经过m次的自然迭代,则可以轻易求得以原初始状态Zn为起点的迭代序列有限集合s1,以及以运算后的结果Zoμ为初始条件的迭代序列s2。
s1: {Zn,Zn+1,Zn+2,Zn+3,…,Zn+m};
s2: {Zoμ,Zoμ+1,Zoμ+2,Zoμ+3,…,Zoμ+m},Zoμ=Oμ。
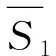
其集合S1和S2的构建以外接矩形为例,如图2所示。图2和图3中:黑点表示有限的庞加莱映像;矩形
表示按照特定方向最小外接矩形构造的凸集;圆点表示以原初始条件映射序列的有限元素集合s1;三角形表示运算后的值为初始状态的映射序列有限元素集合s2;菱形表示最小凸集的几何中心。
以迭代计算前后的结果为起始点所构造的两个凸集的集合关系,如图3所示。此时:若有S2∈S1,则算法必然稳定;若有S1∉S2,则可以判定为算法失稳。当结果如图3(a)所示时,运算可以连续压缩平衡点所在区间,多次迭代后可得到有效的近似平衡点;当集合包含关系如图3(b)所示时,算法处于失稳状态;图3(c)和图3(d)所示情况说明,已经达到计算机的或者程序求解的精度极限,或者原初始状态已经超出原平衡点的吸引域,并呈现指数发散状态。对高维度的系统,可以利用迭代映像在不同相平面上的投影来构建所需要的两个凸集,并结合图3所对应的集合关系判断算法的有效性。
基于上述的特点,无论庞加莱映射发散与否只要转换矩阵的特征值不存在大于1的正实数,可以在判断原算法失效的条件下,改用多次迭代的凸集几何中心或者若干次庞加莱映射的重心替代原算法中的圆心Oμ,作为迭代运算的结果,如式(23)或式(24)所示。
(23)
(24)
当离散样本数量m较大时,理论上对各种基于周期运动发生的分叉都具有较好的收敛性和较为普遍的适应性。
2 近似特征值的数值计算
对平衡点的分析主要分析其雅可比矩阵的特征值,确定近似平衡点特征值也是十分重要的工作。可以采用第1章提供的迭代方法求得在系统Λε中的近似平衡点Zn。
此时,可以保证‖Zn‖足够小,假设存在若干初始状态Zkn属于列向量组Zsn,Zsn及其Zkn满足式(25)所示的条件。
(25)
式中,E0=e0I,e0为对每个初始状态Zn预设的初始误差量,I为单位矩阵,且有rank(I)=rank(Zsn)。
对初始状态组Zsn和Zn取相同次数的庞加莱映射,可以得到关于近似不动点和初始状态组的映射结果,Zsn+m及Zn+m,误差关系可表示为
(26)
式中,Em为m次复合映射后的误差矩阵,根据离散系统的稳定性理论,可以利用式(27)确定雅克比矩阵的所有特征值。
(27)
方程γm=1在复数域内具有m个解,其解集γ的表达式为
(28)
假设近似平衡点Zn处的特征值λ的真解如式(29)所示。
λ=ρcosΦ±jρsinΦ
(29)
式中:ρ为特征值的模长,ρ=‖λ‖;Φ为特征值在复平面内的角度。根据复数的乘积运算,特征值的m次幂可以表示为
λm=ρm{cos[mod(mΦ,2π)]+
jsin[mod(mΦ,2π)]}
(30)
通过对复数取根式可以得出的模接近真值,但是其角度信息并不一定正确。其中,当m=1时可以近似确定辐角位置,但是当m=1时的精确性较低,可以利用复数的指数运算规律,通过迭代法,分别运算m=[1,2,3,…]时的情况,利用渐近性的原理逐步逼近系统雅可比矩阵特征值的辐角真解,根据式(31)的迭代过程算法可以求得特征值辐角逼近解。
(31)
式中:Φm为m次误差迭代对应的特征值辐角;Φ(m)为逐步逼近的不动点雅可比举证的特征值辐角。
3 算例分析
3.1 算例模型
以下以一种含间隙两自由度弹簧非线性柔性碰撞振动系统在含三倍谐波的情况下的动力学研究分析为例,对其中某个类似Flip-NS型余维二的分叉过程进行研究。
选取算例的力学模型如图4所示。图4中:M1和M2为振子的质量;C1,C2和C为阻尼器的阻尼系数;K1,K2和K为弹簧的刚度系数;D为静止状态时的振子间的间隙;g为振子之间的实时动态间隙,负值表示压缩量;F为外激励;FD和-FD为由于弹簧的含间隙接触缘故造成的作用与反作用力。由此可以建立系统的微分方程式(32)。
(32)
式中:弹簧刚度系数Kn具有非线性表达式(33);外激励F含有高次谐波成分如式(34)所示;FD表达式如式(35)所示。
(33)
式中,χ为非线性刚度比例系数。
(34)
式中:P为无量纲的比例系数;Pn为谐波强度;φn为n次谐波的相位。
(35)
由于间隙造成系统中含有一个非光滑切变界面ΣC,如式(36)所示,在其两侧系统的微分方程不连续。为保证系统状态穿越界面ΣC的必然性,参考线性系统对间隙D做出约束,在此将弹簧力学性能曲线进行近似线性替代,并假设外激励只存在主谐波,即理想化假设K1,2,3(Δ)=kn,F=P1cos(ω1t+φ1)。
ΣC:X1-X2=D
(36)
假设系统位移的稳定待定解如式(37)所示。
(37)
式中,A1,A2,B1和B1为解的待定系数,将其代入方程并分离三角函数的相关项可得系数的平衡表达式(38)。
(38)
其中,
在线性近似条件下系统振动时可穿越切变截面的充要条件如式(39)所示。
(A1-A2)2+(B1-B2)2>D2
(39)
根据表达式(38)并定义间隙系数δ表征静态间隙量D,满足如式(40)所示的关系。
(40)
取模型参数:M1=50;M2=4.5;k1=500;k2=1 244;k=2 244;χn=500;C1=0.3;C2=20.03;C=5.4;δ=0.007;ω=15.23;P1=0.128 0;P2=0;P3=0.154 4;φ1=0.24;φ2=0;φ3=0.63。
以RK-4数值积分法进行仿真,采用稳定的二分法进行求解穿过非光滑转折界面的时间间断点,求解精度取1×10-13。以系统主谐波外激励周期定义庞加莱截面Σ如式(41)所示,在数值积分的过程中,利用庞加莱截面法构建离散映射。
Σ:mod(ωt,2π)=φ1
(41)
3.2 分叉分析
通过数值仿真可以得到如图5所示的系统分叉图,具有双稳态的特征。图5中:灰色分支的分叉过程比较明确,是单周期运动失稳以激变的方式演化为拟周期运动,在拟周期区间发生的锁相等行为也极其明确;黑色分支在P=12.5附近出现从拟周期演化为二倍周期运动的分叉过程,从分叉过程推断,该分叉具有Flip-NS分叉的趋势,但是由于本系统得不到系统的解析映射,故而无法利用解析映射的特征值来定义该分叉过程的类型。
利用第1章提供的方法,可求得图5中所对应两支分叉过程的平衡点变化规律,如图6所示。通过对比图5和图6可以看出,第1章所提供的方法对基于单周期运动的分叉具有良好的适应性,平衡点的激变过程和图5中的激变过程相一致。图中求解结果显示,对基于多周期运动的分叉过程适应性不足,这是由于方法机制所导致,对于多周期运动,可以通过构建复合映射的方式将其转化为单周期运动,以便于研究。但是对于混沌运动,由于混沌运动的沥遍性,该方法已经失效。
同时可以看出,对于图5中存在疑点的分叉区间,图6中对平衡点的求解是收敛且稳定的,可以继续利用第2章提出的迭代方法求得系统雅可比矩阵特征值的近似值。对平衡点的求解精度取1×10-13,然后对该近似平衡点的特征值进行37次迭代运算,求得系统的雅可比矩阵特征值变化如图7所示。
图7中,当P=12.5时,不动点的雅可比矩阵其中一对共轭特征值处于单位圆外部,具有明显拟周期运动的特点,和理论分析的结果相一致。随着参数的递增,其雅可比矩阵特征值的虚部分量逐渐减小为0,直接导致系统的庞加莱映像由拟周期状态迁变为二倍周期状态。可以看出,始终仅仅有一对特征值在单位圆附近变化,并不符合发生Flip-NS组合分叉时两对特征值同时穿越单位圆的特点。
上述分叉过程从分叉图的变化规律分析,基本符合Flip-NS分叉的特征,但是从图7内特征值的变化规律中可以看出,其中一对复共轭特征值在单位圆外侧退化为重实特征值,然后其中一个特征值从-1处穿越单位圆,该变化规律符合Hopf分叉周期二锁相状态的特征,其演化过程如图8所示。
4 结 论
本文总结和分析了振动系统中不能利用数值解进行定性分析的现象及其原因。本质原因是现行的定性分析方法对解析解的依赖;关键原因是无法利用数值解求得庞加莱映射的平衡点。文中对上述问题做出了针对性研究,总结了基于数值解求解平衡点及其庞加莱映射特征值的方法,并针对一个存在疑点的分叉行为成功地进行了分析。
文中提到的方法在算例模型上的实践被证明是可行有效的,非线性系统的数值解和非线性定性理论之间可以实现对接,利用差分和迭代原理基于数值解可以完成非线性系统的定性分析,摆脱在定性分析时对解析解的依赖。
