基于数据驱动的SEIQRW新冠肺炎模型及最优控制
2022-09-24李淑萍
苗 慧,李淑萍
(中北大学 理学院,山西 太原 030051)
0 引 言
从2019年起,由严重急性呼吸综合征冠状病毒2(SARS-CoV-2)引起的新冠肺炎在世界各地大规模流行.据世界卫生组织WHO报告数据来看,截至2022年1月17日,全世界累计确诊329 109 769例,死亡555 3630例.全球新冠肺炎病例不断增加,全面了解它的传播途径,采取对应的防控措施非常重要.研究表明,呼吸道飞沫和直接接触是新冠病毒传播的主要途径[1-2],且新冠病毒在物体表面也能存活数天[3],因此,人类通过间接接触被污染的物体表面也可能会导致感染[4-5].
专家学者对不同地区新冠肺炎的传播进行了数学建模.Wang Liyan等在扬州疫情的基础上考虑了潜伏期和治愈期所服从的新密度函数,以及感染模型中的疫苗接种效应,研究了长潜伏期新冠肺炎的传播机制,认为通过足够的隔离和高接种疫苗措施可促使疫情消失[6].Kolebaje O T等提出了一种结合非药物干预措施的新冠肺炎SEIIAQHR数学模型,其中S代表易感者,E代表潜伏者,I代表感染者,IA代表无症状感染者,Q代表隔离检疫者,H代表住院者,R代表恢复者,并将此模型用于研究一些非洲国家的累计确诊病例数的时间序列演变[7].Shen Zhonghua等考虑了巴基斯坦的新冠肺炎报告病例,建立了带有疫苗接种V仓室的SVEAIR模型(A为无症状感染仓室),并进行最优控制分析[8].Abioye A I等建立了带有隔离仓室的SEIQR模型,并结合戴口罩、积极筛查检测、控制社交距离等严格的控制策略,预测尼日利亚的新冠肺炎将被根除[9].
上述模型有的考虑了隔离检疫,有的考虑了疫苗接种,但没有考虑环境病毒对疫情传播的影响.自新冠疫情爆发以来,我国政府采取了一系列隔离防控措施,如通过建立火神山医院集中隔离收治患者[10],并取得了很大的成效.因此,本文建立了一个隔离仓室Q的SEIQR模型.另外,近期的深圳疫情很可能是由国外入境的新冠病毒污染物品引起的[11],本文将研究环境病毒W对新冠肺炎传播的影响,以期为政府部门制定防控策略提供理论依据.
1 模型的建立
S(t)为t时刻易感者数量,E(t)为t时刻潜伏者数量,I(t)为t时刻感染者数量,Q(t)为t时刻隔离检疫者数量,R(t)为t时刻恢复者数量,W(t) 为t时刻环境中的新冠病毒数量,模型仓室图如图1 所示.图1 中,Λ为总人口的输入率,β1为潜伏者对易感者的传染率,β2为染病者对易感者的传染率,β3为环境中的新冠病毒对易感者的传染率,μ为自然死亡率,k为潜伏者到染病者的转化率,b为染病者隔离检疫的比例系数,α为染病者的因病死亡率,γ为染病者的恢复率,δ为隔离后的康复率,m为潜伏者向外界环境释放病毒的速率,μ1为环境中新冠病毒的自然死亡率.模型为
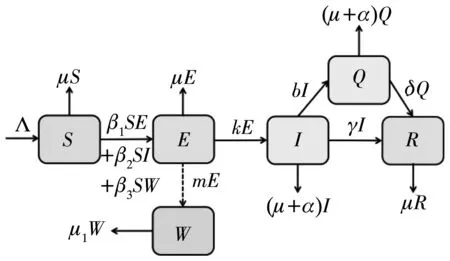
图1 SEIQRW流程图Fig.1 Flow chart of SEIQRW transmission
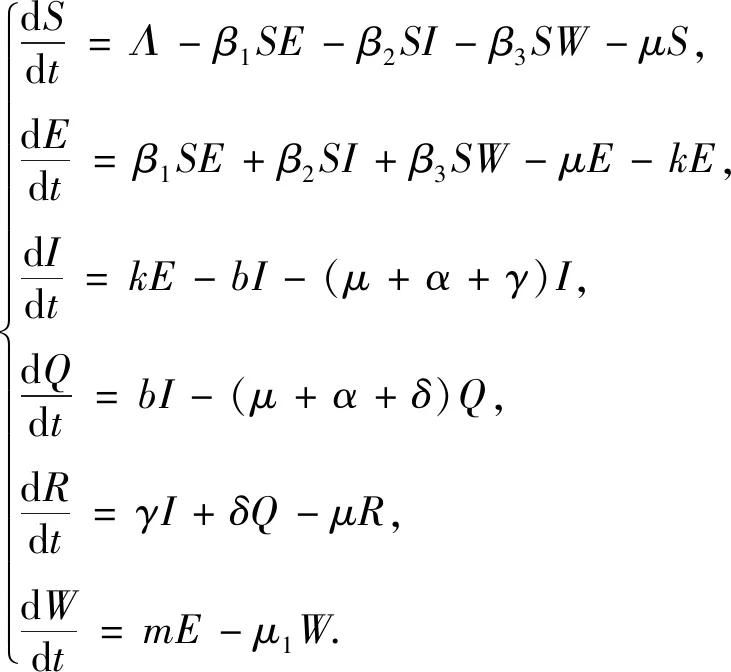
(1)
由N=S+E+I+Q+R得

(2)

Ω={(S,E,I,Q,R,W)|S,E,I,Q,R,W≥0,
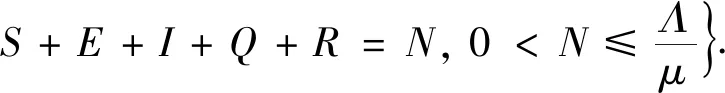
(3)
2 平衡点和基本再生数的计算
利用下一代矩阵法[12],系统(1)中受感染的相关仓室可写为
式中:X=(E,I,Q,W)T;F为新感染的矩阵;V为仓室个体转移矩阵,则

在无病平衡点E0处对(E,I,Q,W)求偏导,可得
计算得

因此,基本再生数为
为求解正平衡点,令模型(1)右端为0,则
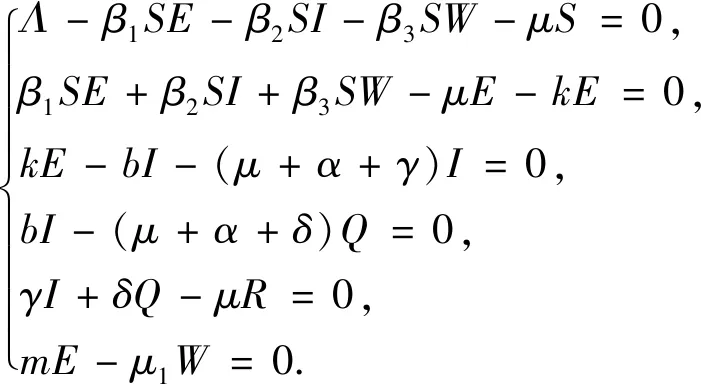
(4)
当R0>1时,正平衡点为E1=(S*,E*,I*,Q*,R*,W*).其中,

3 平衡点的稳定性分析
3.1 无病平衡点的稳定性
定理 1当R0<1时,系统(1)的无病平衡点E0在Ω内是局部渐近稳定的;当R0>1时,无病平衡点不稳定.
证明系统(1)在E0的Jacobian矩阵为
J|E0的特征方程为
(λ+μ)2(λ+μ+α+δ)(λ3+a1λ2+
a2λ+a3)=0.
(5)
显而易见,λ1,λ2=-μ,λ3=-(μ+α+δ).
其中,
μ1+b+μ+α+γ>0,
a2=(μ+k)(b+μ+α+γ)+μ1(μ+k)+
μ1(b+μ+α+γ)>0,
a3=μ1(μ+k)(b+μ+α+γ)(1-R0)>0,
μ1(b+μ+α+γ)2>0.
由Hurwitz判据[13]可知,无病平衡点E0在可行域内局部渐近稳定.
定理 2当R0<1时,系统(1)的无病平衡点E0在Ω内是全局渐近稳定的.
证明可以将原系统(1)的染病仓室重新表示为
x′=(F-V)x-f(x,y),
(6)
式中:x=(E,I,Q,W)T为染病仓室中的人群;y=(S,R)T为非染病仓室中的人群,f(x,y)=(0,0,0,0)T.
运用矩阵理论中的Perron特征向量[14],非负矩阵V-1F的左特征向量ωT对应的特征值为ρ(V-1F)=ρ(FV-1)=R0,可求得ωT=(β1,β2,0,β3).若f(x,y)≥0,F≥0,V-1≥0,则定义Lyapunov函数为
Q=ωTV-1x=
当R0<1时,
Q′=ωTV-1x′=
(R0-1)ωTx-ωTV-1f(x,y)=
(R0-1)(β1E+β2I+β3W)≤0.
所以,当R0<1时,无病平衡点X0在Ω内全局渐近稳定.
3.2 正平衡点的稳定性
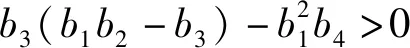
b1=A+B+C+μ+μ1,
b2=A(B+C)+(A+C)μ1+(B+C)μ+μμ1+
b3=ABC+(AB+AC)μ1+Cμμ1+Aμ1β1S*+
b4=ABCμ1+ACμ1β1S*,
A=β1E*+β2I*+β3W*,
B=μ+k-β1S*=[kμ1β2(μ+k)+
mβ3C(μ+k)]/Ζ,
C=b+μ+α+γ,
Z=μ1β1C+kμ1β2+mβ3C.
证明系统(1)在E1处的Jacobian矩阵为
J|E1的特征方程为
(λ+μ)(λ+μ+α+δ)(λ4+b1λ3+b2λ2+
b3λ+b4)=0.
(7)
显然,λ1=-μ,λ2=-(μ+α+δ).b1,b2,b3,b4>0,且有
b1b2-b3=(A+B)a2+ABμ+ACμ+AC2+
μ1(A+C)(C+μ+μ1)+μ(B+C)(C+μ+
μ1)+μμ1(μ+μ1)+Aμβ1S*+(C+μ1)·
4 最优控制策略
为找到合理有效的控制策略,本文采用最优控制理论[15],并运用庞特里亚金极大值原理[16]找到模型中最优控制所需要的条件.
在系统(1)中引入3个控制项u1,u2,u3,将控制系统表示为
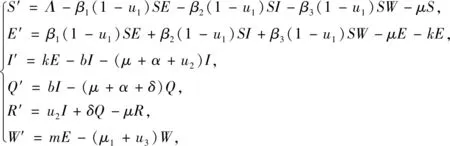
(8)
式中:u1为减少易感者与新冠病毒的直接接触和间接接触的隔离策略;u2为增强感染者的治疗恢复率的治疗策略;u3为消灭环境中病毒的环境卫生策略.
控制函数集为
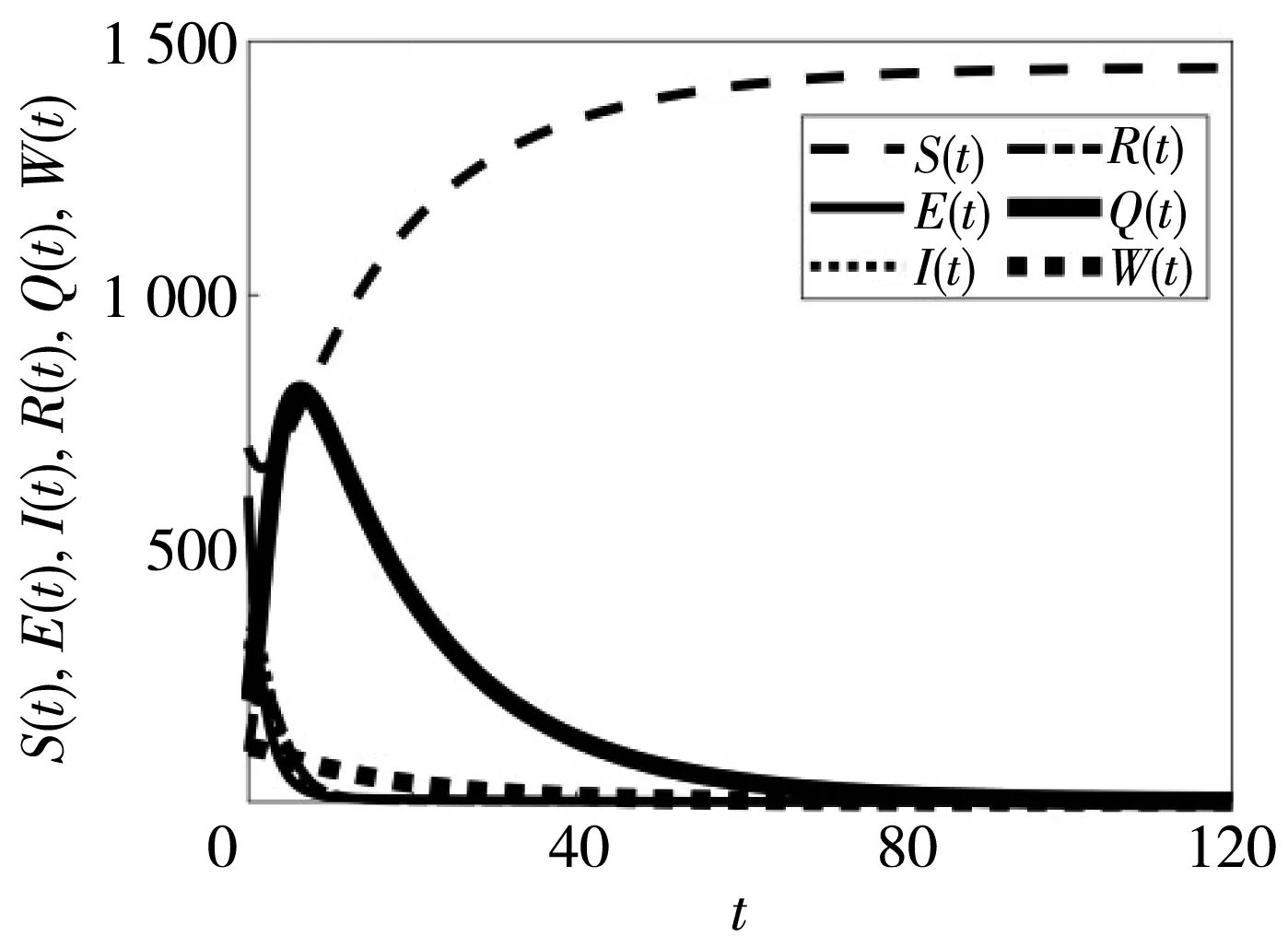
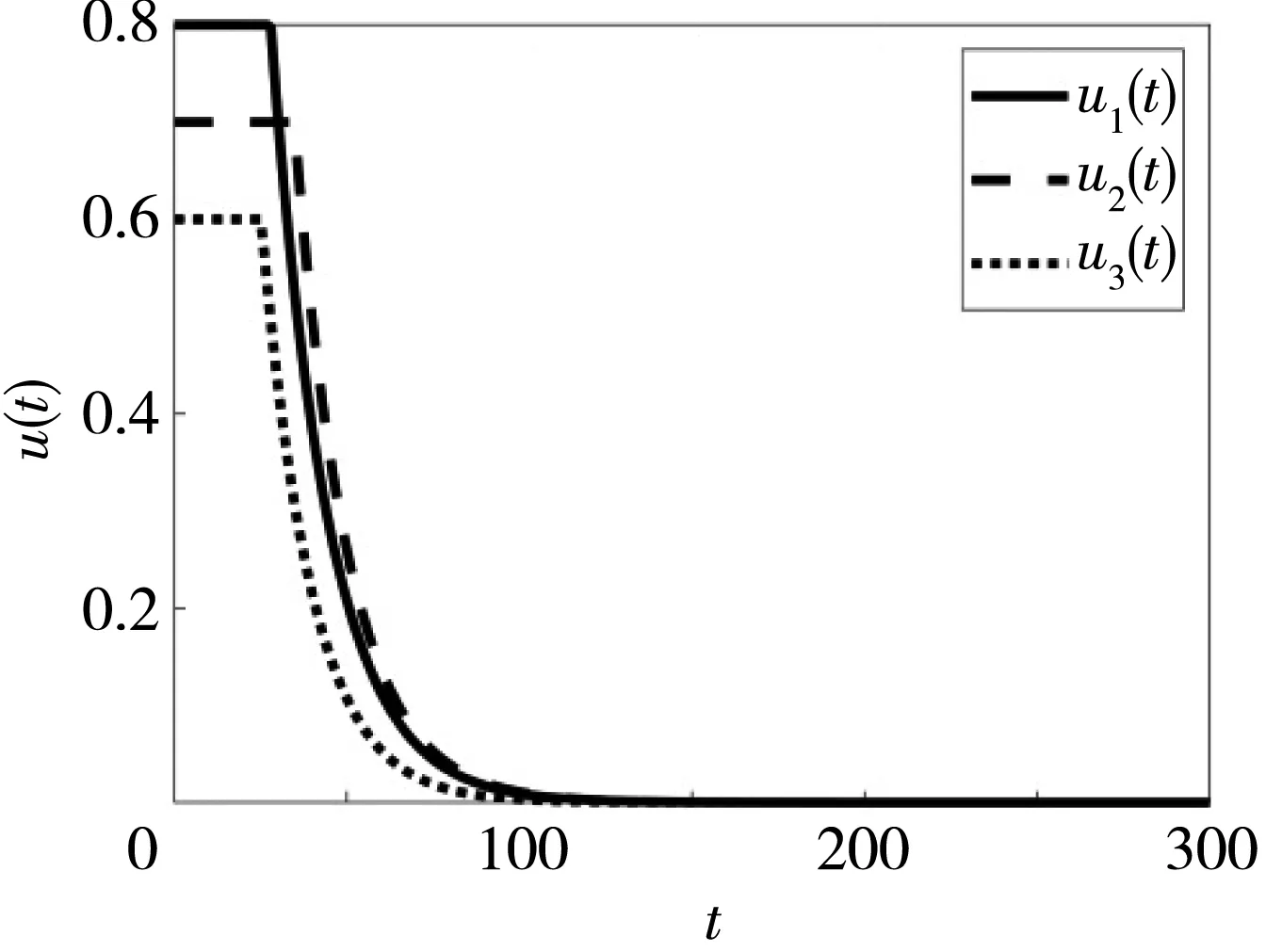
U={U(·)∈L1([0,T];R3)|0 umax<1,∀t∈[0,T]}. 为考虑感染者的治疗成本和控制成本,将目标函数定义为 (9) 庞特里亚金极大值原理是将式(8)和(9)转化为一个关于控制变量的最小化的哈密顿问题,构造哈密顿函数,即 (10) 式中:λi(i=1,2,…,6)为伴随变量. (11) 那么,最优控制为 证明由伴随系统(11)得 根据最优化条件 得最优控制值为 假设Λ=100,β1=0.000 2,β2=0.000 1,β3=0.000 05,μ=0.069,μ1=0.06,γ=0.04,k=0.69,b=0.7,α=0.006 6,m=0.009,δ=0.83,可得R0=0.56<1,如图2(a)所示,验证了无病平衡点是全局渐近稳定的. (a) R0<1 假设β1=0.000 9,β2=0.000 2,β3=0.000 05,m=0.09,b=0.07,δ=0.63,可得R0=3.28>1,如图2(b)所示,故地方病平衡点是全局渐近稳定的. 基于政府在新冠肺炎疫情前期采取隔离防控措施时感染者的数据以及部分参数估计[17],得到k=1/5.2,γ=1/7,α=0.043,δ=1/10,并且假设Λ=3 000,β1=0.65×10-5,β2=0.85×10-5,β3=0.59×10-6,μ=0.06,μ1=0.056,m=0.89,b=0.07.运用Matlab模拟对比了有无考虑环境病毒时估计的染病者人数曲线,如图3 所示,发现带病毒项的系统与实际感染人数更相符. 图3 带病毒、不带病毒的模型与患病人数拟合Fig.3 Fitting model with and without virus to number of sick people 运用PRCC法进行敏感性分析,可以更好地观察各个参数与基本再生数R0的相关性,如图4 所示.可知参数Λ,β1,β2,β3,m与R0呈正相关,μ,μ1,k,b,α,γ与R0呈负相关.这也说明了直接和间接接触都加速了病毒传播,而控制接触和消灭环境病毒可降低基本再生数,从而减少感染人数. 图4 R0与参数的相关性Fig.4 Correlation between R0 and parameters 利用前后扫描法和四阶龙格库塔公式进行模拟,为控制成本,节约医疗资源,令u1=0.8,u2=0.7,u3=0.6,得到最优控制函数图,如图5(a) 所示.令Λ=100,β1=0.000 2,β2=0.000 1,β3=0.000 05,μ=0.069,μ1=0.06,m=0.009,k=0.69,b=0.7,α=0.006 6,γ=0.04,δ=0.83,计算得R0=0.56<1.如图5(b)和(c),当加入控制时,感染人数和环境中病毒数量在较短时间内迅速减少为0,由此可知,最优控制策略可以阻断新冠肺炎的传播. (a) 控制变量u(t)与t的函数关系 本文建立了一个包括隔离和环境中新冠病毒仓室的模型,通过动力学分析,得到基本再生数R0、无病平衡点和正平衡点的稳定性及最优控制策略.基于数值模拟对理论分析进行了验证,参数的敏感性分析和数据拟合进一步证实隔离是疫情防控必不可少的措施.将环境病毒考虑在内可使得模型曲线与患病人数更加接近,强调了环境病毒在疫情传播过程是不可忽视的.如果不在模型中纳入环境间接传播,会导致低估疫情的严重程度.研究结果为世卫组织建议的洗手和表面清洁和消毒的做法提供了强有力的支撑,也为我国采取及时隔离的政策提供了理论依据.
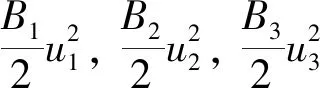
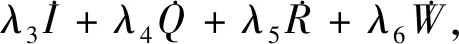
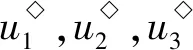

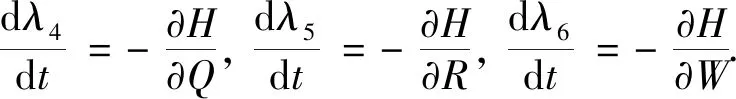

5 数值模拟
5.1 平衡点的稳定性
5.2 数据拟合

5.3 敏感性分析

5.4 最优控制
6 结 论
