林碧凤

（南安市洪新中学，福建 南安 362300）

荷兰数学家弗赖登塔尔曾提出，几何直观可以告诉我们哪些属于可能重要及有意义或者是可接近的，并能够让我们在课题、概念及方法的荒原上不必陷于歧途。而希尔伯特在其所著《直观几何》里面提到：依靠直观想象，我们可以阐述几何中的各类事实与问题，且在许多情况下可用几何轮廓描述相关研究，而避免对严格定义实际计算的累赘阐述。《义务教育数学课程标准（2022 年版》也提到：几何直观重点借助图形描述和分析问题，它能够让原本复杂的数学问题变得简明而形象，帮助学习者探索解决问题的理想思路，并对结果加以预测。

一、几何直观的定义及价值

（一）几何直观的定义

几何直观指的是利用图形，以及图形的关系、变化、运动轨迹等，比较直接地理解问题本质，并得到解决问题的解决思路，产生推断问题结论的直观性较强的感觉及思维方式，通常其为依托与利用图形所进行数学各项内容的思考和想象。

（二）几何直观的价值

数学内容普遍具有双重性，既具有数的特征，又具有形的特征。从双重性视角去客观而全面地认知数学能增进学生对数学本质意义的理解。在这方面，几何直观能力有着独特优势，它能够帮助揭示研究对象的性质与关系，让科学正确的世界观与方法论被学生所认可与接受。几何直观的价值可总结为下述四点：

1.理解价值。理解价值，即借助几何直观实现对抽象数学概念、定义、定理、公式等的直观化与可视化转化，使他们能明确数学概念、定义等的内涵、外延，并了解相关概念的异同点，且对定理、公式由来、推断过程以及适用范围等加以理解。

2.发现价值。可借助几何直观发展观察力与分析力，有助于学习者直接发现新结论、新思路、新方法等。

3.解决价值。可通过几何直观整合数学问题有效信息、将其中的数学模型抽象出来，继而找到处理问题的思路。

4.创新价值。创新价值，即在几何直观的帮助下，让学生拥有创新机会，在提升抽象力的前提下发现创造性思维［1］。

二、试题命制角度的几何直观能力培养

（一）几何问题原型

案例1.如图1 所示，现在已经知道AB=12，AB⊥BC 于点B 位置，AB⊥AD 于点A 位置，且AD=5，BC=10，CD 中点是E，那么AE 长度是多少？

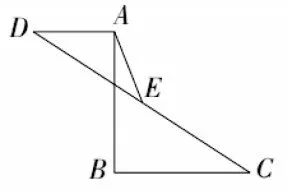
图1

【解法分析】该题的命制从学生几何直观能力形成与应用方面提出的。首先，在学生意识到问题中给出“AD=5”“BC=10”“CD 中点是E”这些条件后，很容易想到中位线定理的知识；其次，题目中的“AB 和BC 在B 点垂直”“AB 和AD 在A 点垂直”则属于极具典型性的平行线条件，也容易联想到平形四边形相关知识点。该题考查学生的几何直观能力，若是可以快速找出题图与平行四边形的联系，如图2 所示，该题的解答会非常简单。

图2

【理论分析】初中生在处理几何试题时，若遇到稍显复杂的问题，一般情况下会利用作辅助线的方法，而简单辅助线并不足以支撑几何直观能力形成，此时教师可尝试使学生转换思维，借助基本图形叠加法，让原本复杂的图形趋于简单化。几何直观需要以特定的几何背景为条件才能产生效果，即几何直观需要以几何图形为载体。以本题为例，题目中给出的几个条件看似简单，实际上恰可以充当展现几何直观能力的背景，也就是能够暗示学生发掘“背景”中的内在含义、引申含义等。再者，几何直观对象普遍具有可视性和层次性，本题的点和线特殊位置关系巧妙之处在于：学生可利用已知垂直条件联想到平行，再利用连接右上角部分“缺失”的做法，把图形“补充完整”，整个过程是可视的、有层次的，最终能够转变为有效的“新对象”。最后，几何直观致力于揭示探索对象的性质与关系，在看似简单的图形中进行基于几何直观的高级、抽象空间形式转化，本题符合这一要求，可让图形在重新加工后以新图形面貌出现，从而让题目变得直观易解。

总之，从几何直观能力定义的角度看，该问题利用图形直观的位置关系构造平行四边形，从而得到问题的解决思路。从试题命制的角度看，该图形的直观性较强，通过对中点与中位线定理之间的联系达到对本题涉及的多个数学知识点进行合理的思考与想象，从而培养学生的数学思维能力。

（二）几何问题拓展

除了基本问题外，中学数学教师还可以在考核学生“几何直观”能力的试题命制时，注意拓展问题的价值，以便给学生提供足够丰富的研究材料。现以两个问题为例，对几何直观能力价值与应用进行分析。

案例2.如图3 所示，在矩形ABCD 中，以BC 为直径，绘制半圆O，OE⊥OA 于点E，对角线AC 同半圆O 另一交点是P，在连接AE 后，请证明AE 为半圆O 切线，另外，若PA=2，PC=4，那么AE 长度是多少。

图3

【案例分析】对于第一个问题，可基于构造不同几何模型的策略，给出不同解法。例如，学生可在教师的提示下，先做辅助线OF⊥AE 于F，从“一线三直角”模型，得到△ABO∽△OCE，再引出，继而得出△ABO∽△AOE，借助角平分线性质，便可证明OF=OB，接下来的过程可由学生自主推导，教师进行从旁的适时提醒。

对于第二个问题，相对而言难度较大，因为已知与所求间关系不是特别明显，入手不易，此时建议学生从已知出发，考虑到BC 为直径，P 为圆周上点，所以可以联结BP，产生△ABP∽△ACB 的结论，顺势求出AB，从而得到BC、BO，再借助△ABO∽△AOE，顺利解决问题。让学生在此过程中感受几何直观能力的应用技巧，从而进一步提高学生的几何直观能力。

【策略归纳】本题属于圆的综合题，如果站在知识角度分析，可看到它比较直接地考查了切线判定与性质、矩形性质，以及相似三角形和全等三角形等方面知识，若基于思想方法进行探讨，可注意其涉及转化法和截长法、补短法等，而如果从几何变换、几何模型角度分析，又有对翻折变换及等腰三角形等知识点。一般而言，有效提高和拓展几何直观能力，不仅要从问题中的知识角度进行综合分析，更要掌握数学思想方法的应用。

（三）几何问题进阶

案例3.图4 中，△ABC 为等腰直角三角形，其中∠BAC=90°，如果把△ABC 绕点C 进行顺时针旋转，可产生△A'B'C，标记旋转角α，若90°＜α＜180°，作A'D⊥AC，A'和B'C 相交点E。在∠CA'D=15°时，试作∠A'EC平分线EF，使之交BC 于点F。请写出旋转角α 是多少度，并尝试求证EA'+EC=EF。

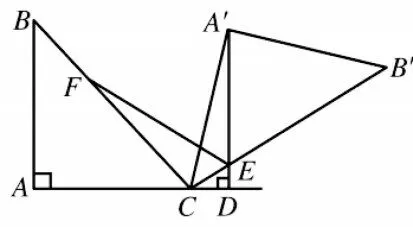
图4

【案例分析】在原有条件下，设P 为直线A'D 上一动点，再将PA 与PF 连接起来，在AB=2 的情况下，得到线段PA+PF 最小值。原问题与拓展问题相结合，是一道既有较强综合性，又有较大难度与较高灵活性的几何试题。

几何问题进阶绝不是简单直观就可以捕捉到解题方法。只有从基本几何模型出发，基于直观能力添加模型常用辅助线，并做更进一步的具体分析，才能有效解决问题。

三、启示

经对两个综合性较强问题的分析可知，一些试题命制非常注重考查学生对几何基本知识与基本技能的掌握。且十分关注学生在几何证明基本方法及对应变换方面的能力，包括图形平移、旋转，以及对轴对称的利用等，其可给教师培养学生几何直观能力进一步启示［2］。

其一，几何直观能力对于描述、分析问题很重要，对于解决问题也很重要。切实加强几何直观教学，可有效增强学生兴趣、提高学生学习能力。优化几何基本图形及基本结论教学，对于几何教学，以及代数、统计和概率教学等均可成为基础与重点，其为培养以几何为载体解题能力的前提。

其二，几何变换是图形关系研究的重要手段，是初中阶段的核心数学学习内容之一。几何变换包括全等变换与位似变换等几何变换知识，其中全等变换中包括平移、旋转、翻折等变换形式。

其三，在平面几何中，像各类试题中的平行线内的M 角模型、三角形中的中点模型、角平分线中的对称全等模型等，均可以帮助学习者处理综合问题，快速发现突破口。因此加强数学模型意识，可以让其几何直观、逻辑思维等各项能力得到潜移默化进步［3］。

其四，一题多解、一题多变以及多题一解等解题方法，可培养学生创新意识.在此过程中，多种数学思想、数学方法将得到应用，如数形结合思想、转化思想、和差法、割补法等。

四、总结

几何直观能力一方面涉及数学知识探究过程，另一方面因其抽象性、动态性、模型性，有助于学生将复杂问题简单化，促进其学习效率的提升。从试题命制角度出发培养几何直观能力，是一种正本清源的做法，希望能够给相关教育工作提供一些参考。