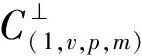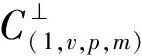一类三重循环码及其重量分布
2022-09-16刘芳蕊范翠玲
刘芳蕊,范翠玲
(西南交通大学 数学学院,成都 610031)
假设p是一个素数,有限域GF(p)上的[n,k,d]线性码是n维向量空间GF(p)n中的一个k维线性子空间,其中非零向量汉明重量的最小值为d。若有限域GF(p)上的[n,k,d]线性码C,满足(c0,c1,…,cn-1)∈C⟹(cn-1,c0,c1,…,cn-2)∈C,则称C为循环码。若将任意向量(c0,c1,…,cn-1)∈GF(p)n等价地表示为多项式的形式,即c0+c1x+c2x2+…+cn-1xn-1∈GF(p)[x]/(xn-1),则任意有限域GF(p)上长度为n的线性码C对应于商环GF(p)[x]/(xn-1)中的一个子集,线性码C是循环码当且仅当GF(p)[x]/(xn-1)中对应的子集是商环GF(p)[x]/(xn-1)的一个理想。众所周知,GF(p)[x]/(xn-1)的每一个理想都是主理想。假设C=〈g(x)〉是一个循环码,其中多项式g(x)是首一的且是C的所有生成元中次数最小的,则g(x)是唯一的并称它为生成多项式,称h(x)=(xn-1)/g(x)为C的校验多项式。若有限域GF(p)上长度为n的循环码C的校验多项式h(x)为GF(p)上t个不同的不可约多项式的乘积,则称对偶码C⊥有t个零因子。
令Ai表示长度为n且汉明重量为i的码C的码字个数,那么码C的重量计数器定义为如下表达式:1+A1y+A2y2+…+Anyn。重量分布A0,A1,…,An是编码理论中一个重要的研究课题,它不仅包含用来估计纠错能力的重要信息,还可以计算在一些算法下检错和纠错的出错概率[1]。另外,循环码具有丰富的代数结构,因此重量分布在数论上是一个有趣且具有挑战性的问题。循环码具有高效的编译码算法,因此被广泛应用于消费电子、数据传输技术、广播系统和计算机应用等领域。此外,具有较少重量的循环码在认证码里有着重要的应用,可以很容易地计算出由这些循环码构造的认证码的参数[2]。同时,具有较少重量的循环码在密钥共享方案也有着重要的应用,可以很容易确定由这样的循环码生成的秘密共享方案的访问结构[3-5]。具有较少重量的循环码在跳频序列的设计中有着特殊的应用[6-7],三重循环码在联合方案也有应用[8]。因此,研究具有较少重量循环码是十分具有价值的工作。
本文提出了一类新型p元(p是一个奇素数)三重循环码,它的对偶码有2个零因子,并利用指数和理论完全确定了这类循环码的重量分布,证明了其中一些循环码是最优的。
1 符号和定义

2 对偶码有2个零因子的循环码
给定正整数m,q=pm且n=q-1,令α是乘法群GF(q)*的1个生成元,对于任意的0≤a≤q-2,将α-a在GF(p)上的极小多项式记为ma(x)。
假设0≤u≤q-2和0≤v≤q-2是任意2个满足Cu∩Cv=∅的整数。C(u,v,p,m)表示GF(p)上长度为n,码字为
c(a,b)=(c1,c2,…,cn),∀(a,b)∈GF(p)×GF(p)
(1)
3 一些已知的三重循环码
Carlet等[3]和Yuan等[21]采用一些特殊的单项式构造了一些循环码并证明了以下定理。
定理1假设m≥3为奇数且p为奇素数,当v=(ph+1)/2,p=3,gcd(m,h)=1且h是奇数,或者v=ph+1时,则码C(1,v,p,m)是一个三重[pm-1,2m]循环码,其重量分布如表1所示。当m是偶数,定理1中由单项式xv定义的循环码C(1,v,p,m)有5个非零重量。关于定理1中三重循环码的对偶码的信息,读者可以参考文献[3]。

表1 重量分布1
Luo和Feng[22]扩展了定理1中的第一个构造并且证明了以下定理。
定理2假设m≥3是奇数且p是奇素数,如果v=(ph+1)/2,其中h是一个满足gcd(2m,h)=1的整数,那么码C(1,v,p,m)是一个三重[pm-1,2m]循环码,其重量分布如表2所示。

表2 重量分布2
文献[23-24]中介绍了几类三重非二元循环码,本文不需要这些码的重量分布公式,因此不再赘述。同样地,本文仅考虑三重非二元循环码,不会涉及引用三重二元循环码。
4 一类三重循环码及其重量分布
本节将提出一类定义在有限域GF(p)上的三重循环码C(u,v,p,m),其中u=1,v是使得Cv∩C1=∅且lv=m的整数。容易验证,循环码C(1,v,p,m)的长度为q-1,维数为2n。
4.1 引理
首先介绍2个有限域上指数和的引理。
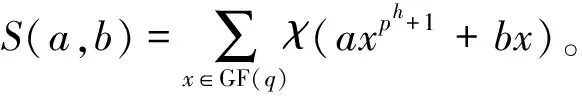
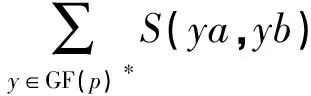
表3 指数和的值分布
证明根据S(a,b)的定义,可得

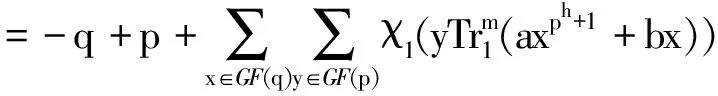
=-q+p+(q-1-Wa,b)p
=(p-1)q+pWa,b
(2)
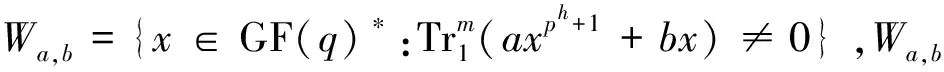
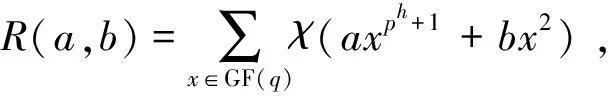

表4 指数和的值分布
证明当h是偶数时,结论在文献[20]中的定理3.4中已证。现假设h是奇数,则在GF(p)中存在一个非平方元λ满足λ(ph-1)/2=-1,根据R(a,b)的定义,可得
(3)
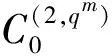
(4)

根据式(3)和(4)可得:
=2(p-1)q+2pWa,b,
(5)
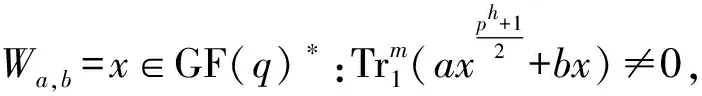
根据指数和的理论,循环码C(1,v,p,m)中的一个码字c(a,b)的汉明重量wt(c(a,b))可表示为:
(6)
其中,对每一组(a,b)∈GF(p)2,
(7)
对于给定的v,在本节中出现的函数Tv(a,b)均为(7)所定义的指数和。
下面的引理将用于下文中确定本文提出的一类循环码的重量分布。
引理3设s为满足gcd(q-1,s)=2的任意整数,则
其中λ为GF(p)*中任意给定的非平方元。

(8)
显然,gcd(q-1,s)=2。当x遍历GF(q)时,xs将遍历GF(q)中的非零平方元2次,且仅0出现1次。类似地,λx将遍历GF(q)中的非平方元2次,且0仅出现1次。引理3的结论由(8)得。
4.2 一类三重循环码
下面的定理为本文主要结果。
定理3假设m为奇数,p=5且v=(5m-1)/4+(5(m+1)/2-1)/2。码C(1,v,p,m)是一个GF(5)上参数为[5m-1,2m]的循环码且其重量分布如表2所示。
证明假设h=(m+1)/2且s=5h-1。因为m为奇数,所以gcd(s,pm-1)=2。容易验证,v为奇数且sv≡2(mod 5m-1)。令λ=2为GF(pm)上的一个非平方元,则2v≡-2(modp)。根据引理3,有:
(9)

由(6)式和(9)式可得:
(10)
码C(1,v,5,m)的重量分布可由式(10)和引理2直接得到。
例1 假设p=5,m=3且v=43,则C(1,v,p,m)是GF(5)上的一个参数为[124,6,90]的循环码,重量计数器为1+3720y90+9424y100+2480y110。
例2 令p=5,m=3且v=483,则C(1,v,p,m)是GF(5)上的一个参数为[3124,10,2450]的循环码,重量计数器为1+2030600y2450+5860624y2500+1874400y2550。
5 三重循环码在密钥共享中的应用
密钥共享是密码学中一个有趣的课题。在一个密钥共享方案中,管理者将创建一个密钥,以便在一组参与者之间共享。管理者将计算每个参与者共享的密钥,并分发给所有参与者。一些参与者能够在合并他们的密钥后恢复整个密钥,而一些参与者将无法恢复。本节将研究基于本文中提出的三重码的密钥共享方案。
5.1 一种基于线性码的密钥共享方案
设G=[g0,g1,…,gn-1]是GF(p)上的一个[n,k,d]线性码C的生成矩阵。本节中提到的所有线性码,假设没有任何生成矩阵的列向量是零向量。利用线性码构造密钥共享方案如下:
1)密钥和参与者:在由线性码C构建的密钥共享方案中,密钥是GF(p)的一个元素,有n-1个参与者P1,P2,…,Pn-1和一个管理者。
2)共享密钥的计算和分配:为了计算关于密钥s的共享密钥,管理者随机选择一个向量u=(u0,…,uk-1)∈GF(p)k,使得s=ug0,GF(p)k中一共有pk-1个向量u∈GF(p)k。然后管理者将u视为一个信息向量,并计算相应的码字t=(t0,t1,…,tn-1)=uG。最后,对于每个i≥1,把ti交给参与者Pi作为共享密钥。
3)恢复密钥:注意到t0=ug0=s,一组共享密钥{ti1,ti2,…,tim}确定这个密钥当且仅当g0是gi1,…,gim的线性组合。
下面的引理表明了哪些参与者可以恢复密钥[5]。
引理4设G是GF(p)上[n,k]码C的生成矩阵。在基于C的密钥共享方案中,一组共享密钥{ti1,ti2,…,tim}可以确定这个密钥当且仅当对偶码C⊥中有一个码字
(1,0,…,0,ci1,0,…,0,cim,0,…,0),
(11)
其中至少存在一个j使得cij≠0,1≤i2<… 若一组参与者可以通过组合他们的共享密钥来恢复该密钥,则包含该组的任何一组参与者也可以恢复该密钥。若一组参与者可以用他们的共享密钥来恢复该密钥,但其任何真子集的共享密钥的组合都不能恢复该密钥,则他们被称为最小访问集。此处的一组参与者的一个真子集的包含的成员更少。因此,仅需研究最小访问集,要确定这个集合,需要定义最小码字。 一个向量c∈GF(p)n的支撑集定义为{0≤i≤n-1:ci≠0}。如果c2的支撑集包含c1支撑集,则码字c2包含码字c1。若一个非零码字c只覆盖它的倍数,但不覆盖其他的非零码字,则称它为最小码字。若最小码字的第一个坐标为1,则称为最小AS码字。 根据引理4和上面的讨论,最小访问集和对偶码C⊥的最小AS码字集之间存在一一对应关系。为了确定密钥共享方案的访问结构,只需要确定最小AS码字集,即所有最小码字集的一个子集。然而几乎在每一种情况下,只要能够确定最小AS码字的集合,就应该能够确定所有最小码字的集合。 参与者的共享密钥取决于码C的生成矩阵G的选择。根据引理4,G的选择并不影响密钥共享方案的访问结构。因此,下文将称之为基于C的密钥共享方案,而不提及用于计算共享密钥的生成矩阵。 定理4[5]设C是GF(p)上的一个[n,k]码,并设G=[g0,g1,…,gn-1]是它的生成矩阵。若C的每个非零码字都是一个最小向量,则在基于C⊥的密钥共享方案中,一共有pk-1个最小访问集。此外,有以下结论:1)若gi是g0的倍数,其中1≤i≤n-1,则参与者Pi必定在每一个最小访问集中。这样的参与者称为独裁者;2)若gi不是g0的倍数,其中1≤i≤n-1,则参与者Pi必定在pk-1个最小访问集的(p-1)pk-2个中。 根据定理4,若对于一类码的每一个非零码字都是一个最小向量,则研究这一类码的构造是一个有意义的工作。由这类线性码给出了一个密钥共享方案,并且这一密钥共享方案具有定理4中描述的较好的访问结构。 若一个线性码的任意两个非零码字的重量足够接近,则这一个码的每一个非零码字都是极小的。下面的引理说明了这一性质。 引理6在本文构造的循环码C(1,v,p,m)中,每一个非零码字都是极小的。 证明本文中提出的循环码C(1,v,p,m)具有参数[pm-1,2m],且其重量分布如表2所示,其中p≥3。 若码的重量分布如表2所示且m≥3,则类似地可以验证如下的不等式成立: 由引理5,引理结论得证。 证明根据引理4和引理5,本定理的结论得证。 对于本文中提出的许多循环码,其素数p为5,导致空间p太小。在实际应用中,一个密钥空间应尽可能大。使用本文提出的码所构造的密钥共享方案,利用编码的规则将密钥空间中的每个元素编码为GF(p)上元素构成的一个序列,然后参与者依次共享序列中的每一个元素。
5.2 基于特殊线性码的密钥共享方案的访问结构
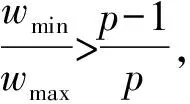
5.3 本文中的线性码构造的密钥共享方案的访问结构