李春雷于凤来

数学理解水平的划分

李春雷1，2，于凤来3

（1．北京师范大学 教育学部，北京 100875；2．北京师范大学良乡附属中学，北京 102488；3．山东省莒县阎庄街道中心初级中学，山东 日照 276535）

基于经典的数学理解内涵的阐释以及已有各家理解水平的划分，将学生数学理解划分为工具性理解、关系性理解、创造性理解、文化性理解4个水平，并以均值不等式为典型案例，详细解读学生各数学理解水平的内涵和表现形态．工具性理解水平的价值不能忽视．学生个体数学理解水平是发展变化的，学生间的数学理解水平是有差异的．在力所能及的范围内，鼓励学生追根问底式地深层次学习，达到“关系理解”的水平；鼓励学生对知识进行自我建构，达到“创造性”理解水平；鼓励学生在历史文化、审美情趣、人文关怀中进行熏陶，达到“文化性理解”的水平．

数学理解；工具性理解；关系性理解；创造性理解；文化性理解

信息时代知识记忆、数据计算的大部分功能可以由计算机代替，人的核心竞争力主要体现在对核心问题的理解力、创新力方面．理解是教育的永恒追求，数学理解是国际数学教育的重要研究主题．有效的数学教学需要认真致力于发展学生对数学的理解[1]．基于经典的数学理解内涵的阐释以及已有各家理解水平的划分，将学生数学理解划分为工具性理解、关系性理解、创造性理解、文化性理解4个水平，以核心数学知识均值不等式为典型案例，解读各数学理解水平的内涵．

1 数学理解的内涵

1971年，英国数学教育家、心理学家斯根普指出，理解某事意味着将它同化成适当的图式，这说明理解具有主观性[2]．新知识进入现有的认知结构或者促进认知结构的转变，学习者才能理解知识．希尔伯特和卡彭特将数学理解看作是表征数学概念、数学事实的内部网络的结果，如果数学的内部表征成为个人内部知识网络的一部分，则数学被个人理解了；而如果数学知识和已有的网络由更强或者更多的关系联结着，则说明这个数学概念、数学事实或思想被人彻底地理解了[3]．1978年，格里诺认为，数学理解是一个过程，代表某种概念的关系结构能够被理解[4]．1991年，皮瑞和基伦将数学理解当作一种整体的、动态的、层次的、非线性的、超验回归的、内在化的心理过程[5]．分析以上研究者对理解内涵的剖析可知，尽管有人认为理解是一种过程，有人认为理解是一种结果，但有着共同之处或相似之处，“图示”“认知结构”“知识网络”“关系”“联结”“整体”成为了理解涵义的关键词，都在于“认知结构”状态的描述．

西蒙将教师当作数学理解的主体，认为数学理解是指教师根据学生的行为经验建立一个连贯和具有潜在价值的组织，能将学生已有知识经验转变为学生的数学能力[6]．梅耶基于学生的视角，认为理解是学生创造性地利用呈现的信息去解决问题的能力[7]．数学理解的主体是教师还是学生，是教师对数学本体知识的理解，还是教师对学生数学理解的把握，或是学生对数学的理解？这个问题必须要搞清楚．数学理解水平的划分关注的是学生数学理解水平的把握和判断．

学生数学理解是指学生对数学本质的认识，知道数学概念、定理、公式、符号、思想方法、应用、创造的真实样态，知道所学习的数学对象是什么、为什么、还能探究什么的一系列知识与技能．学生数学理解对象的核心是概念和关系．学生对数学概念的理解是指知道数学概念的定义、内涵（如概念的特征和性质）、外延（如分类与分类标准）、来源的真实样态．学生对关系的理解是指知道数学定理、法则、公式及其推导过程，知道数量关系、图形关系、随机关系等数学研究对象之间相互关系的真实样态．

2 数学理解的层次划分

1976年，斯根普将理解分为工具性理解（instrumental understangding）和关系性理解（relational understanding）两种模式[8]：前者是知道事物是什么，但不知为什么；后者是既知道事物是什么，也知道事物为何这样，它揭示了数学知识的发生过程和逻辑规律，蕴含着一定的数学思想．1982年斯根普将数学理解又细分为工具性、关系性、逻辑性和符号性理解4种模式．

1978年，巴克斯顿将理解划分为死记硬背（rote）、观察（observational）、深刻理解（insightful）和逻辑理解（formal or logic understanding）4个水平[9]．

1982年，比格斯和科利斯描述的SOLO理论[10]，将学习者对某一个具体问题的反应水平分为前结构水平（prestructural）、单点结构水平（unistructural）、多点结构水平（multistructural）、关联结构水平（relational）、拓展抽象水平（extended abstract）5个不同的层次[11]（见图1）．其中单点结构、多点结构、关联结构依次表示学习者只知道一个相关方面、知道几个相关方面、知道将几个相关方面形成一个整体的结构；最高理解水平为拓展抽象，代表学习者能够调用头脑或题目中的多个认知素材，得到的结论或观点具有高度概括性、抽象性、衍生性、新颖性．

图1 SOLO分类理论的5种水平

1987年，格里诺和赖利将数学原理划分为3个逐渐复杂的理解水平：可以依据原则解决问题但缺乏对原则认识的“遵从水平”，可以完成性能评估判断性任务和应用问题但只可意会不可言传的“隐性理解水平”，能够口头陈述知识原则和程序结果的“显性理解水平”[12]．

1988年，皮瑞—基伦建立的“超回归”数学理解模型[13]（图2），将数学理解分为8个水平，分别为初步了解（primitive knowing）、产生表象（image making）、形成表象（image having）、关注性质（property noticing）、形式化（formalizing）、观察评述（observing）、组织结构（structuring）和发明创造（inventing）．将“发明创造”作为理解的最高层次，用返回原处揭示数学理解的非单向性．

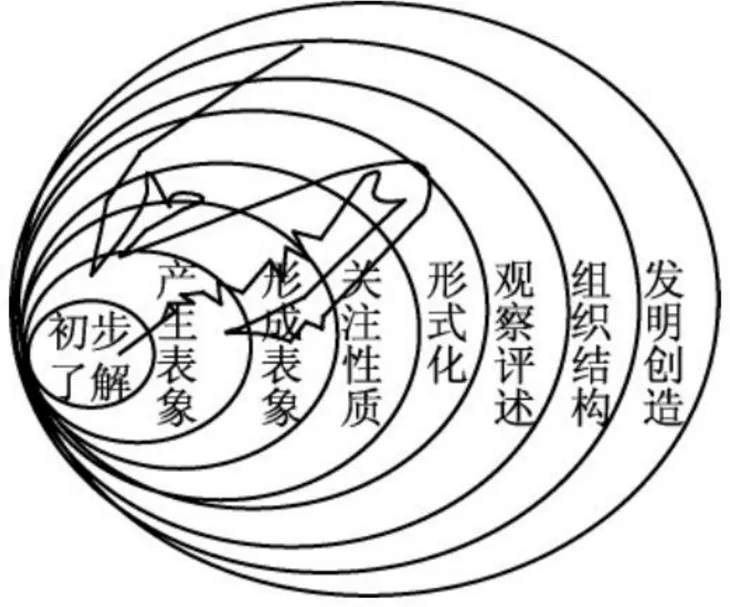
图2 皮瑞—基伦理解模型

1998年，威金斯和麦克泰格指出，理解包括解释（explanation）、释义（interpretation）、运用（application）、洞察（perspective）、移情（empathy）和自知（self-knowledge）6个维度[14]．这种分类综合了个体所展现的认知理解、学习的迁移以及情感共鸣．

2006年，索耶强调了概念理解的重要性，指出在今天的知识经济时代，仅记忆事实性知识和程序性知识远远不够，重要的是能对复杂概念形成深刻的概念性理解，并能基于这些理解生成新的观点、新的理论、新的产品和新的知识[15]．

2012年，扎尔曼·尤西斯金在第12届国际数学教育大会（ICME12）上，发表了题为“什么是对数学的理解？”的研究报告，将数学理解划分为算法技能、性质证明、应用情境、隐喻表征、历史文化共5个维度[16]．

2009年，巩子坤构建了包括直观理解、程序理解、抽象理解、形式理解的数学理解模型，认为形式理解是基于逻辑推理，来证实运算结果的合理性[17]．2012年，徐彦辉认为数学理解包括记忆性、解释性、探究性3种方式[18]．2013年，匡金龙等将数学理解划分为经验性、形式化、结构化、文化性共4个理解层级[19]．2014年，王瑞霖等确立的数学理解层次结构的理论模型，包括表象理解、解释理解、建立联系、思想运用和创造生成5个层次[20]．2018年，谷晓沛等将函数概念的理解水平确定为感知水平、释义水平、关联水平、抽象水平[21]．

从以上学者对数学理解的分析来看，数学理解水平是有层次之分或阶段之分的，但分类标准的不同，语义内涵的不同，导致分类结果的不同，也导致对学习者数学理解水平评价时，仁者见仁，智者见智．应借鉴整合已有研究成果，寻找数学理解层级的字面语义与内涵能够较好统一、主体层级少而精、层级鉴别方法比较清晰的分类方法．

斯根普早期将数学理解分为“工具性理解”和“关系性理解”两种模式；皮瑞—基伦建立的“超回归”数学理解模型中的最高层级为“发明创造”，不妨将其称为“创造性理解”；匡金龙等将数学理解的最高层级认定为“文化性理解”．将数学理解划分为“工具性理解”“关系性理解”“创造性理解”“文化性理解”，能否较好统摄以上各家的分类方法？分析见表1．

2.1 “工具性理解”的统摄性

“工具”，人们能够识别它，对外懂得它有什么用途，知道怎样用，记住操作步骤就可以了，而不太关心它的内部构造．斯根普认为“工具性理解”是知道事物是什么，但不知为什么，将“工具”一词运用到“数学理解”的最低层次，语义上也达到了生产“工具”与数学问题解决“工具”内在意蕴的吻合．学者们所划分的“死记硬背”“观察”“单点结构”“遵从”“隐性理解”“初步了解”“产生表象”“形成表象”“关注性质”“记忆事实性知识和程序性知识”“算法技能”“符号性””“直观理解、程序理解”“记忆性”“经验性理解”“表象理解”“感知”水平，都能被较好地统摄到“工具性理解”水平．

2.2 “关系性理解”的统摄性

“关系”，代表至少两个事物之间具有的联系，而不是事物孤立的存在．斯根普认为“关系性理解”既知道事物是什么，也知道事物为何这样．斯根普后来细分的“逻辑性”水平和其他学者划分的“深刻理解”“逻辑理解”“多点结构”“显性理解”“形式化”“观察评述”“结构化”“解释”“释义”“性质证明”“组织结构理解”“建立联系”“思想运用”水平，都能被较好地统摄到“关系性理解”水平．

2.3 “创造性理解”的统摄性

创造性、创新性反映了从无到有、从有到新的过程．学者们划分的“关联结构”“拓展抽象”“发明创造”“运用”“洞察”“自知”“生成新的观点、新的理论、新的产品和新的知识”“应用情境”“隐喻表征”“抽象理解”“探究性”“创造生成”“关联”水平，都能被较好地统摄到“创造性理解”水平，代表学习者发现了数学对象间的不易被察觉到的关系，建立了研究对象的远距离联系，能将所获得的数学结论进一步推广到更大领域，面对种种不确定性和非连贯性能够自发地创造．

2.4 “文化性理解”的统摄性

数学不仅蕴藏着强大的理性精神，也彰显着巨大的人文情怀．扎尔曼·尤西斯金划分的最后一个维度“历史文化”水平，威金斯和麦克泰格划分的“移情”水平，都能被较好地统摄到“文化性理解”水平．移情是指一种能深入体会他人的情感和观点的能力，促使学习者能够从多个角度思考问题，开阔胸襟．

综上所述，“工具性理解”注重的是数学结论的事实性及其简单应用性，“关系性理解”注重的是数学知识获得的过程性及其结构性，“创造性理解”注重的是数学知识的关联性及其扩展性，“文化性理解”注重的是数学发展的历史性和人文性．因而可将学生“数学理解”的水平从时空上划分为“工具性理解”“关系性理解”“创造性理解”“文化性理解”4个水平．前3者是从空间维度阐释数学理解的由浅到深、逐渐复杂的层次水平，最后者是从时间维度、历史角度、精神层面、审美情趣视角阐释数学理解的层次水平．

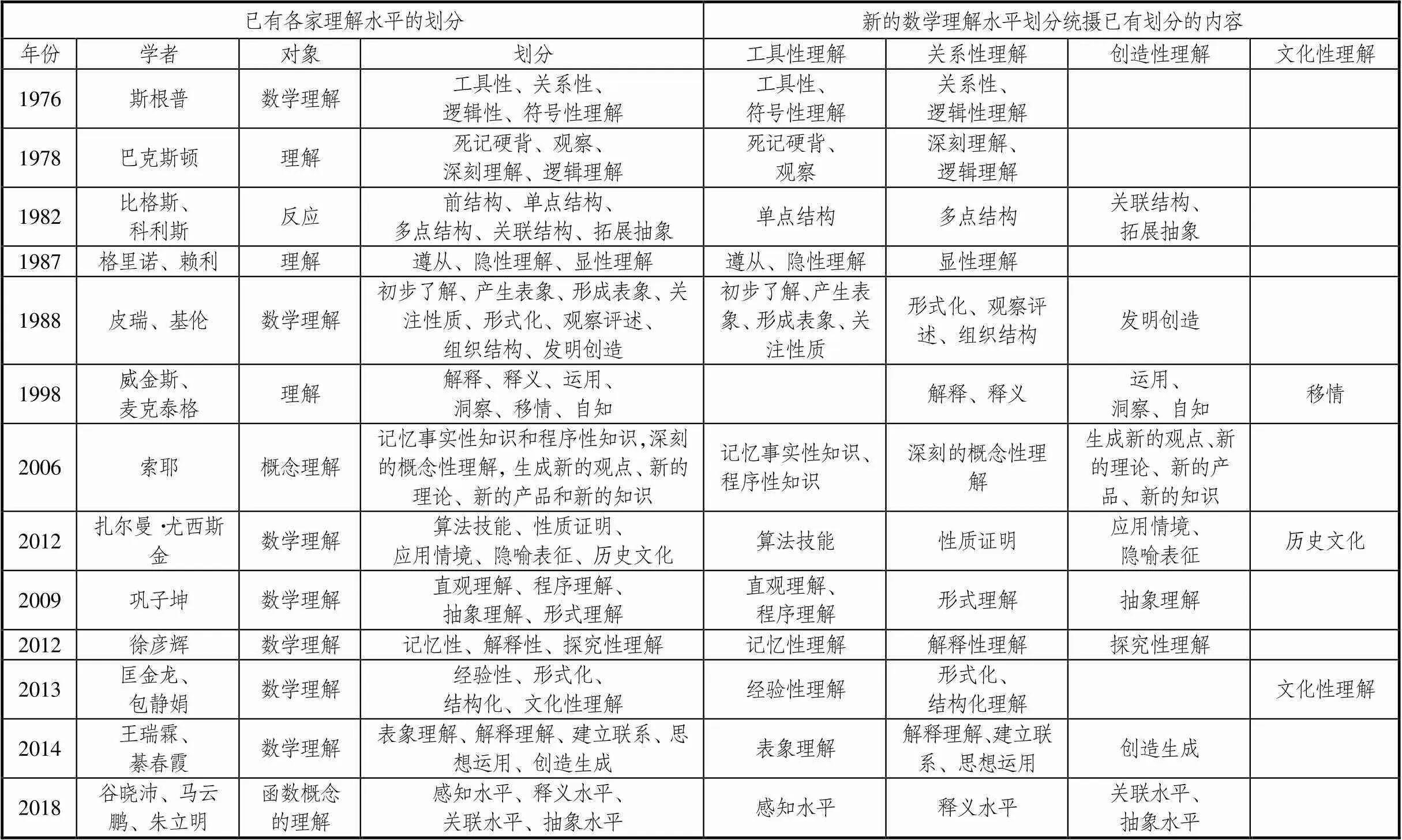
表1 新的数学理解水平划分对已有观点的统摄对照

3 案例解读学生数学理解水平的层次划分

3.1 工具性理解水平

工具性理解表现为“知其然，不知其所以然”．工具性理解水平的学生，知道符号所指代事物的意义，或是一种程序性的关于规则如何操作．工具性理解涉及的知识较少，短期内有作用，但长期内作用有限；需要记住数学知识，加重了记忆负担．工具性理解水平有以下表现形态．

理解事实性知识是什么．学生知晓数学研究对象的定义和规律，即对数学概念、理论、思想以及观点等了解，但未能完全认识，乃是一种机械记忆．如学生知道两个正数的算术平均值、几何平均值的概念，知道均值不等式的文字表征：“两个正实数的算术平均值大于或等于它们的几何平均值．”

理解知识属性是什么．学生在已有认知的基础上，基于数学活动经验，能梳理、归纳、概括事物的某些特征与规律，知道一些属性，能够描述其意义，具有鲜明的个性化特征．如学生知道均值不等式是一个绝对不等式．

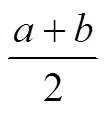
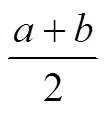
理解知识的功能是什么．学生能够说明其作用，简单初步使用该对象的某些性质，解决一些封闭性数学问题．如学生见到问题：“对于均值不等式，它有什么用？你想一想可以研究哪些问题？”能够回答出均值不等式可应用于大小的比较、求函数的最值以及值域、求解参数的取值范围等．

理解操作程序是什么．学生将问题解决算法化，能够按规则运算，依照固定的模式获得正确答案．精确的计算和对各种题型的熟练把握似乎成为数学学习的主旋律，对问题的反应常常停留在死记硬背操作步骤的层次，不明白为什么要采取这样的顺序．如学生知道均值不等式求最值的程序为“一正二定三相等”，并且能够熟练操作，但是不清楚顺序调整将会出现哪些问题．

3.2 关系性理解水平

关系性理解表现为“不仅知其然，还知其所以然”．关系性理解水平的学生，能够对数学定理、原理、规则进行逻辑分析或证明，将数学知识的形成和论证提升为数学思想方法层面，与周围知识进行逻辑联结，将知道的一系列的数学事实构建成知识体系和模型，关系图式是一种高质量的关系组织形式．关系性理解减少了记忆负担，过滤了头脑中无效的信息，适应新任务的能力更强，记忆更长久．关系性理解水平有以下表现形态．

理解证明的过程．学生知道为何一个数学陈述是正确的或者某个数学规则来自哪里，能够逻辑证明数学结论的严密性、正确性．例如对于问题：“想一想均值不等式可以用哪些方法证明？”学生能够给出均值不等式的综合法、比较法、反证法、分析法等证明方法，表明理解了这一不等式成立的根据．

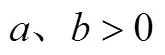
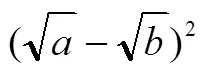
理解数学结构的深化与发展．学生知道新观念能够与哪些已有结构可以融合，将事物按照最简洁、最规则、最协调、最具联系的方式进行组织．从宏观上来看，结构是各要素之间协调与综合关系的组成模式；从微观来看，结构表现为知识间的联系与层次递进；从发展观来看，学生的思维结构和心理结构是不断深化的．如在均值不等式的学习中，学生知道在概念结构系统中，增添了3个新成员，即算术平均值、几何平均值、均值不等式；在运算结构系统中，算术平均值是加、除的运算结果，几何平均值是乘积、开方的运算结果；在数列结构系统中，算术平均值、几何平均值分别是两个正数的等差中项、正的等比中项；在大小的顺序结构系统中，不等号体现算术平均值、几何平均值内在必然的大小关系；在等价结构系统中，“当且仅当”条件就是一种等价关系，“大于或等于”又可以等价表征为“不小于”；在数学思想结构系统中，化归思想、解方程思想、等价转化思想、数形结合思想对于均值不等式的研究至关重要；在数学工具结构系统中，比较两个数或式的大小、求函数的最值或值域问题，又增添了一个工具“均值不等式法”；在不等式结构系统中，均值不等式是绝对不等式，而不是解不等式等．

3.3 创造性理解水平

创造性理解表现为“不仅知其然、知其所以然，还能知新的‘然’‘所以然’”．创造性理解水平的学生，能够将数学观念运用于变式状态下的数学情境，发现数学对象之间的远距离关联，提出新问题，进行新猜想，在新的情境中举一反三，解决一些复杂的问题，对数学知识提出改革建议．创造性理解是超越关系理解的更高级的理解，具有创新的特征．创造性理解水平有以下表现形态．

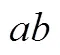
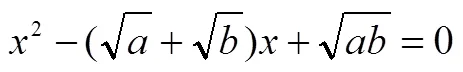
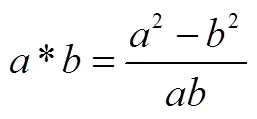
理解数学拓展抽象的意义．学生能够以已有知识、经验或体验为基础，获取新的知识、经验或体验，自我认识、自我反思、自我完善、自我超越、自我创造，成为思考者、发现者、发明者、创新者．学生数学学习的结果，除了获得知识和技能外，还有长时间积累后形成的创新思维模式，达到孔子所说的“从心所欲不逾矩”的境界．如“你能类比两个数的均值不等式，猜测出3个、4个等更多数的均值不等式吗？”学生能够遵循数学知识发展的内在逻辑，扩充均值不等式的维度，升华为个正数的均值不等式．

理解数学在实践中的应用．学生能够将现实中的问题转化成数学模型，在数学与现实的循环中不断生成和重构知识．数学源于现实、寓于现实并应用于现实，应用化的精神是数学的生命，根植于现实中的数学充满着生机活力．如“我们生活中哪些最值问题可以用均值不等来处理？”机器人兴趣小组组长张玉琼（化名）以建机器人场地为背景提出真实的研究问题：“要在科技活动室用屏风围出一个矩形机器人活动场地．（1）若矩形场地的面积为6.25 m2，问这个矩形的长和宽各为多少时，所用屏风最少？最少要购买屏风长多少米？（2）现有屏风长为10 m，问这个矩形活动场地的长和宽各为多少米时，屏风围成活动场地的面积最大？最大面积是多少平方米？”此问题来源于校园真实科技生活，学生能够很快进入研究角色．教育家苏霍姆林斯基说：“智慧出在人的手指尖上，实践操作不仅仅是身体的动作，而且是与大脑的思维活动紧密联系着的．”[22]解决活动场地中的数学最值问题，激发了学生的创新热情．

3.4 文化性理解水平

文化性理解水平的学生，能够理解数学史对观念、精神、思维方式等产生的影响，受到数学家优秀品格的熏陶，进行数学文化的欣赏，在追求数学美的过程中来加深对数学的理解．阿恩海姆指出，一旦达到了对某一范式最简单的理解，它就会显得更稳定、有更多意义、更容易掌握．具有秩序、统一的事物更符合知觉简化性倾向，更易于使人产生审美体验[23]．狄德罗曾指出，数学中所谓美的问题，是指一个难于解决的问题，所谓美的解答，是指一个对于困难复杂问题的简易解答[24]．文化性理解水平有以下表现形态．

理解数学历史发展的脉络．学生知道数学概念、定理与历史上哪些大事件、关键人物相关，能够说数学故事，提炼故事中蕴含的数学思想方法，挖掘故事中孕育的数学精神，注入数学文化意义．如学生知道第24届国际数学家大会2002年在北京国际会议中心隆重举行，会标是以三国时期吴国数学家赵爽的弦图为基础设计的，赵爽的弦图不仅能够证明勾股定理，还能够探究得到均值不等式．

理解数学的人文价值．学生知道数学概念、定理蕴藏的德育价值、人文关怀．如关于均值不等式中等号何时取，学生能用自己父母年龄做实例加以说明．当父母年龄恰好相同时取等号，当父母年龄不同时取绝对不等号，这说明学生关注父母的年龄和生日，有很好的教育意义．

4 数学理解层次划分的反思

学生数学理解水平划分还可做进一步探讨．为便于操作，采用了工具性理解、关系性理解、创造性理解、文化性理解4个水平的划分方法．工具性理解、关系性理解、创造性理解水平是逐步提高的，这三者主要体现在学生认知领域的递进关系．而文化性理解水平主要是体现在情感、态度、审美、意志、价值观领域，是不可或缺的一种理解水平．事实上，可以将学生数学理解的水平划分为两个维度，即认知维度的数学理解水平、情感维度的数学理解水平，在它们的交叉点做更加深入的研究．

学生数学理解水平是发展变化的、有差异的．数学概念的形成和关系的建立具有层次性，因而数学理解不是一蹴而就的，具有动态性、阶段性、渐进性等特征．要接受学生数学理解的差异性，让学生在突破自我中努力达到自己潜在的最高理解水平．在力所能及的范围内，鼓励学生追根问底式的深层次学习，摒弃浮光掠影式的表层次学习，达到“关系理解”的水平；鼓励学生对知识的自我建构，达到“创造性”理解水平；鼓励学生在数学的历史文化中进行熏陶，达到“文化性理解”的水平．

[1] National Council of Teachers of Mathematics. Principles standards and for school mathematics [M]. Reston V A: NCTM, 2000: 18.

[2] Skemp R. The psychology of learning mathematics [M].London: Penguin Books, 1971: 46.

[3] HIEBERT J, CARPENTER T. Learning and teaching with understanding [M] // Douglas A Grouws. Handbook of research on mathematics teaching and learning,New York: Macmillan, 1992: 65–97.

[4] GREENO J. Understanding and procedural knowledge in mathematics instruction [J]. Educational Psychologist, 1978, 12 (3): 262–283.

[5] 余瑶，张春莉．国外数学理解研究的进展与展望[J]．教育学报，2018，14（1）：35–44．

[6] SIMON M. Key development understandings in mathematics: A direction for investigating and establishing learning goals [J]. Mathematical Thinking and Learning, 2006, 8 (4): 359–371.

[7] MAYER R. Models for understanding [J]. Review of Educational Research, 1989, 59 (1): 43–64.

[8] Skemp R. Relational understanding and instrumental understanding [J]. Mathematics Teaching, 1976, 77 (3): 20–26.

[9] BUXTON L. Four levels of understanding [J]. Mathematics in School, 1978, 7 (9): 36–38.

[10] Biggs J B, Collis K F. Evaluating the quality of learning: The SOLO taxonomy [M]. New York: Academic Press, 1982: 13–15.

[11] BIGGS J, WATKINS D. Classroom learning [M]. Singapore: Prentice Hall, 1995: 176.

[12] GREENO J, RILEY M. Processes and development of understanding: In metacognition, motivation, and understanding [M]. Hillsdale: Lawrence Erlbaum Associates, 1987: 293.

[13] 吴骏．小学四年级学生对平均数概念理解的发展过程[J]．数学教育学报，2011，20（3）：39–41．

[14] WIGGINS G, MCTIGHE J. Understanding by design [M]. VA: Association for Supervision and Curriculum Development, 2005: 85–100.

[15] SAWYER R K. The Cambridge handbook of the learning sciences [M]. NewYork: Cambridge University Press, 2006: 2.

[16] Usiskin Z. What does it mean to understand some mathematics [R]. ICME-12, Seoul, 2012: 10–15.

[17] 巩子坤．数学理解说及其理论与课程意义[J]．比较教育研究，2009，31（7）：39–43．

[18] 徐彦辉．数学理解三种方式及其课堂教学特征[J]．中国教育学刊，2012（1）：59–61．

[19] 匡金龙，包静娟．为理解而设计——促进小学生数学理解的教学策略研究[J]．上海教育科研，2013（11）：61–63．

[20] 王瑞霖，綦春霞．数学理解的五层递进及教学策略[J]．中国教育学刊，2014（12）：40–45．

[21] 谷晓沛，马云鹏，朱立明．高一学生函数概念数学理解水平的实证研究——以T城市为例[J]．数学教育学报，2018，27（3）：25–29．

[22] 蔡健飞．小学生数学创新思维的培养[D]．武汉：华中师范大学，2007：45．

[23] 朱黎生，宋乃庆．格式塔美学对数学教学的启示[J]．数学教育学报，2012，21（6）：10–12．

[24] 陈焕斌，张雄．略论数学美的本质属性[J]．数学教育学报，2008，17（5）：28–30．

The Division of the Level of Mathematical Understanding

LI Chun-lei1, 2, YU Feng-lai3

(1. Faculty of Education, Beijing Normal University, Beijing 100875, China；2. Liang Xiang High School Affiliated to Beijing Normal University, Beijing 102488, China;3. Yanzhuang Street Central Junior Middle School of Ju County, Shandong Rizhao 276535, China)

Based on the interpretation of the connotation of classical mathematical understanding and the division of existing understanding levels, students’ mathematical understanding is divided into four levels: instrumental understanding, relational understanding, creative understanding and cultural understanding. Taking the mean value inequality as a typical case, this paper interprets the connotation and manifestation of students’ various levels of mathematical understanding in detail.The value of the level of instrumental understanding cannot be ignored. The level of students' individual mathematical understanding is developing and changing, and the level of students’ mutual mathematical understanding is different. Within the scope of the ability, students are encourage to pursue in-depth learning, to achieve the level of “relational understanding”. Students are encouraged to self-construct knowledge and to achieve the “creative understanding” level; they are encouraged to be nurtured in history and culture, aesthetic taste and humanistic care, so as to reach the level of “cultural understanding”.

mathematical understanding; instrumental understanding; relational understanding; creative understanding; cultural understanding

2022–04–09

北京市教育学会“十四五”教育科研课题——基于高阶能力培养的大单元教学课程设计研究（FSYB2021-002）

李春雷（1967—），男，河北香河人，正高级教师，博士，主要从事数学教育和学生创新能力发展研究．

G447

A

1004–9894（2022）04–0068–06

李春雷，于凤来．数学理解水平的划分[J]．数学教育学报，2022，31（4）：68–73．

[责任编校：陈隽、陈汉君]