李国军,陈东杰,董齐芬,王亢

(1.浙江警察学院公共基础部,浙江 杭州 310053;2.浙江警察学院计算机与信息安全系,浙江 杭州 310053)

1 引言

迭代学习控制(Iterative learning control,简称ILC)适用于在有限区间作重复操作的被控系统,通过反复试验不断调整输入信息来改进输出效果,以便跟踪上期望轨迹[1-2].通过足够多次重复后的ILC具有良好的跟踪性能,所以常被应用于机器人控制,产品流水线控制,间歇过程控制以及电路稳定性控制等场合.传统的ILC在应用时,要求每次的初始定位误差必须等于零或者某个固定值,但这在实际中基本不可能做到,所以说初值问题是迭代学习控制的基本问题之一.因此,研究任意初值条件下的迭代学习控制不仅有必要而且十分有意义.

对于连续系统而言,关于初值研究的文献较多.文献[3]首次引入边界层的概念,并让边界层随着随着时间单调收敛至零,由于控制误差受边界层限定,所以相应的控制误差也渐近收敛至零,但由于边界层只能在时间趋向无穷时才收敛至零,所以这种方法达不到完全跟踪.文献[4-6]利用吸引子方法达到了实际完全跟踪.文献[7-8]采用误差跟踪的方法达到了一致性跟踪,但这种方法在每次迭代时都需要事先重新设定的新的期望轨迹.对于高阶可参数化非线性系统,在控制增益已知的情形下,文献[9]在指定区间达到了精确跟踪.对于带有时变迭代参数的不确定系统,文献[10]利用内模控制方法设计参数学习律,确保系统收敛.在压缩映射方法研究过程中,对于具有高相对阶的系统,文献[11]提出了一种修正方法,在完成对初态误差的修正以后,能够确保系统达到完全跟踪.对带有固定初态误差的高阶多智能体系统,文献[12]用Step-by-step策略逐个修正各个状态偏差并最终达到了一致性跟踪.针对非线性连续系统,文献[13]提出了一种针对任意初态的修正方法,但这种方法不能完全修正初始误差,而且只适用于一阶系统.

对于离散系统而言,近年来研究的学者不多,得到的有益结论并不丰富.对于固定初态情形,文献[14]借助线性矩阵不等式求解控制器增益,并通过反馈辅助控制方法达到了渐近跟踪.对于高相对阶线性离散系统,文献[15]达到了渐近跟踪.而文献[16-17]针对带有固定初态的高相对阶非线性离散系统,在控制时引入初始修正行为,实现了在指定区间上的一致性跟踪.文献[18]提出了一种针对任意初态和时变轨迹的离散自适应ILC方法,能够确保系统沿着迭代轴渐近收敛,沿着时间轴在指定区间内逐点收敛.文献[19]对文献[18]进行了评论,指出了文中的瑕疵.文献[20]针对非参数化非线性不确定离散系统,得到了类似于文献[18]的结论.对于控制方向未知的非线性离散系统,针对任意初态情形,文献[21]中提出的控制策略能够使系统沿时间轴渐近收敛.

本文提出了一种基于压缩映射的迭代学习算法,该算法在任意初态下,能够确保离散时不变时滞系统在指定区间上达到逐点跟踪,最后通过三个例子验证了该方法的有效性.

2 问题阐述及控制器设计

考虑下述线性定常时滞系统

其中,t=0,1,2,···,N;k=1,2,···表示迭代次数;d(为正整数且d＜N-1)是时滞参数;xk(t)∈Rn,yk(t)∈Rr,uk(t)∈Rm(相应可以简写为xk,uk,yk)分别表示第k次迭代的系统状态,控制输入和输出向量.A,B,C是合适维数的系统参数矩阵,并且B右可逆.

设yr(t)(简写为yr)是给定的期望轨迹,设xr(t)(相应简写为xr)是给定的期望状态,ek(t)=yr-yk表示第k次输出误差.

假设2.1初始状态xk(0)随机,状态xk(t)可测,并且xk(-d)=0,···,xk(-1)=0.

为了使得系统(1)能够在指定时间内跟踪上目标轨迹,提出带有初始状态误差修正功能的控制律.

3 收敛性分析

这一节着重分析系统(1)在应用控制律(2)以后的收敛性.本节中定义‖·‖是向量或矩阵的某种范数,对于上节中提出的控制律(2),有下面的定理.

定理3.1如果初始状态是任意有限值,并且存在一个矩阵Γ满足

那么控制律(2)能够让系统(1)在区间[1,N]上达到逐点跟踪.

证明为了方便书写,记

对于系统(1),当t∈[0,N-1]时,应用控制律(2)并根据假设2.1可得

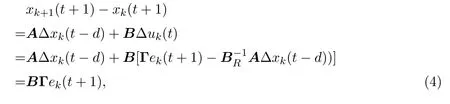
在上式两端同时乘以矩阵C,可得

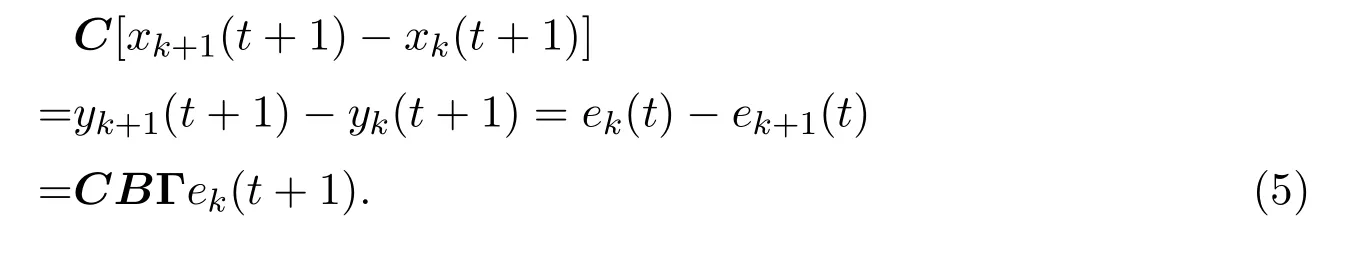
所以有

因此当t∈[0,N-1]并且‖I-CBΓ‖≤1时有

也就是说,在[1,N]上‖ek+1(t)‖逐点收敛于0.

注2.1从上面的证明可知,该算法所决定的系统收敛点与系统的时滞参数d的大小无关.

根据上面的证明可知,对于下面的复杂离散时滞系统

其中,d1,···,dj(1≤di≤N-2,1≤i≤j)是时滞参数,A,A1,···,Aj是合适维数的矩阵,如果该系统迭代初态任意并且矩阵B右可逆,则可以采用下面的控制律使其达到完全跟踪.

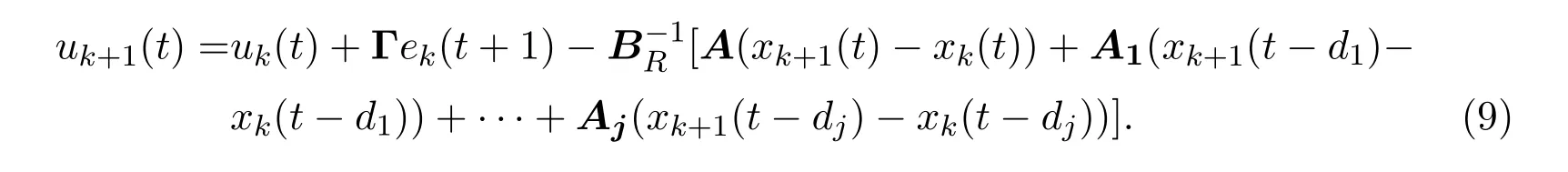
定理3.2如果系统只具有下面的模型

其中,V1(t)是迭代时的固定性扰动,Vk(t)是第k次迭代时的随机性扰动,若

此时应用控制律(2),该系统依然能够稳定.

证明对于系统(10),当t∈[0,N-1]时,应用控制律(2)可得

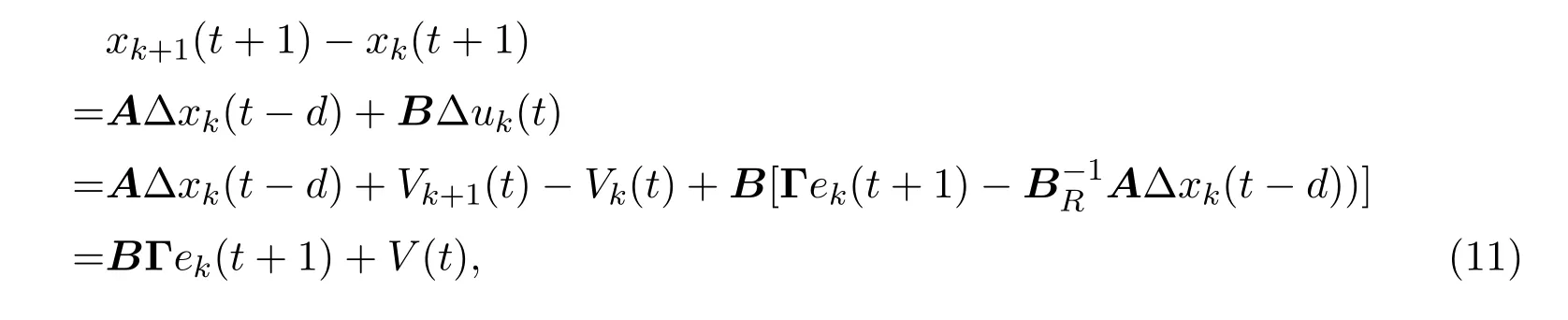
其中,V(t)=Vk+1(t)-Vk(t)是前后两次随机性扰动的叠加,从统计意义上来讲V(t)依然随机,只是该扰动的期望和方差与Vk(t)不同而已.

化简(11)式有

记

当t∈[0,N-1]并且‖I-CBΓ‖≤1时有

因此,在[0,N-1]上‖ek+1(t+1)‖有界.也就是说,在[1,N]上‖ek(t)‖有界,即系统(10)在该区间上稳定.

4 数值仿真

本节将通过三个例子来验证本文算法的有效性,在仿真过程中,例4.1和例4.2的系统采用时间Ts=0.005秒.

例4.1考虑下面的时滞系统

该系统的作业区间为[0,400].

系统运行之前具有随机性较大的初始状态xk(0)=25*rand(rand产生0到1之间的随机数值),控制律(2)中的控制增益Γ=0.89,仿真中迭代次数为15次.系统的跟踪轨迹采用文献[12]中的期望轨迹

从图1放大图中的可知,控制律(2)在t=1*Ts时完成状态修正,完全跟踪上期望轨迹.在图2中,误差统计是从点t=1*Ts开始的,从图中可以看出,只需要迭代4次就基本能完成跟踪.从图3中可以看出,在点t=1*Ts处,控制量uk(t)并没有收敛,而是在t=5*Ts处才开始收敛(仿真和实际情形相差一个单位采样时间,因为MATLAB下标从1开始),这是由于时滞因子所致.

图1 实际轨迹yk(t)和期望轨迹yr(t)

图2 各次迭代实际跟踪误差‖ek(t)‖2

图3 相应的控制量uk(t)

例4.2考虑下面的复杂时滞系统

该系统的作业区间为[0,200].

系统运行之前初始状态为

控制律(2)中的控制增益

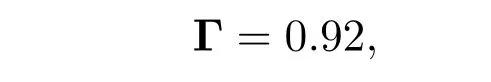
仿真中迭代次数为15次.系统的跟踪轨迹为

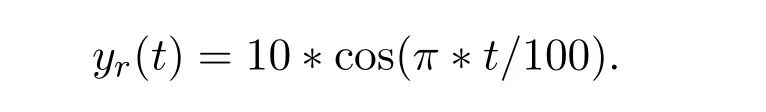
具体仿真结果见图4-图6.

图4 实际轨迹yk(t)和期望轨迹yr(t)

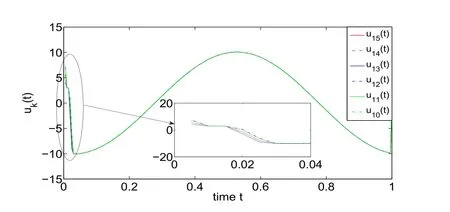
图6 相应的控制量uk(t)

从图4中可以看出,系统收敛的时间点和所有的时滞因子都无关,但控制量的收敛时间点和时滞因子有关.本例中最大时滞因子d2=4,所以系统在t=1*Ts时完成状态误差修正并跟踪上期望轨迹,而控制量在t=5*Ts处收敛.从图6中可以看出,控制量收敛的时间点只和最大的时滞参数有关,与其它时滞参数无关.在图5中,误差统计也是从点t=1*Ts开始.

图5 各次迭代实际跟踪误差‖ek(t)‖2

例4.3考虑类似于文献[13]中的时滞系统

其中,系统运行之前初始状态为

控制律(2)中的控制增益取值如下:

系统的跟踪轨迹如下:

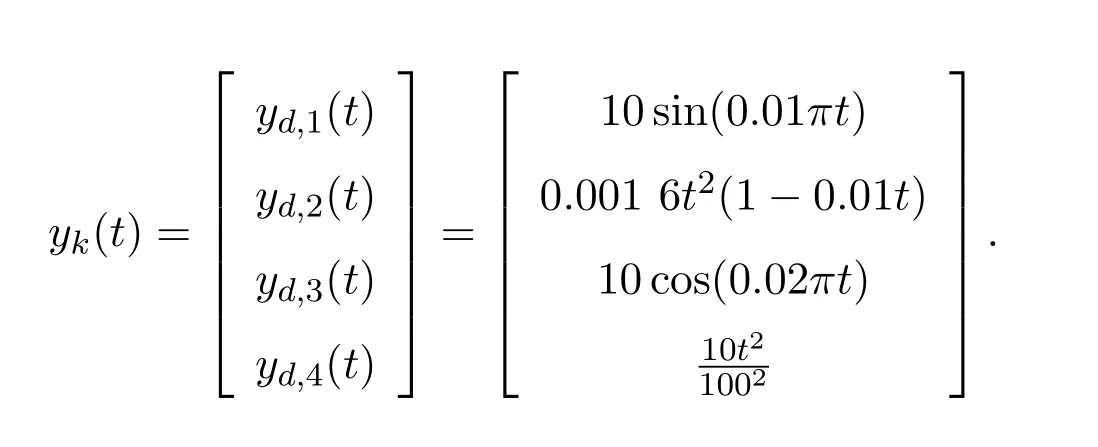
同样引用该文献中的指标来表征迭代学习的控制精度:

仿真中迭代次数为15次,图7和图9是第15次迭代时的结果.

图7 期望轨迹yr(t)和实际轨迹yk(t)

图9 相应的控制量uk(t)

从图7的放大图中可以看出,系统没有达到逐点完全跟踪,但通过图8可知,系统在控制率(2)的作用下能够稳定.

图8 各次迭代实际跟踪误差EE(i)

上面的仿真验证了本文所提算法对于任意初态下的线性离散时滞系统而言,不管系统是否存在随机性扰动,系统都能够稳定.

5 结论

本文讨论了线性离散时不变时滞系统存在任意初态误差的迭代学习控制问题,借助压缩映射手段,提出了一种带有修正项的控制策略.在控制过程中,控制算法可以快速修正初态误差.如果系统没有随机性扰动,当修正好状态误差后,系统能够达到无误差跟踪;如果系统有随机性扰动,则误差位于某个范围内,而且本文也从理论和实践两方面验证了此算法的有效性.对于系统信息不能精确已知的任意初态偏差情形,目前仍无有效方案,后续本人将从事该方面的研究.