谷琼雅,时振华,王丽真,何静

(西北大学数学学院,陕西 西安 710127)

1 引言

近些年,随着分数阶微分方程在工程、物理、生物等领域的广泛应用[1],人们越来越关注分数阶微分方程的研究,其中构造分数阶偏微分方程的精确解是偏微分方程理论研究中非常重要的问题[2-3].大量研究论文已引入多种构造精确解的方法,如不变子空间法[4]、q-HAM方法[4]、齐次平衡法[5]、泛函分离变量法[6]、广义分离变量法[6]等.李对称分析是研究偏微分方程的重要方法和途径.微分方程的不变性质和其所描述的重要的物理现象都与其李对称密切相关.

李对称分析由Sophus Lie在十九世纪首次提出并用于整数阶微分方程的群分析中.随后,文献[7]提出分数阶导数和李对称的分数阶延拓公式,由此李对称分析被推广到分数阶微分方程的研究中.许多学者利用李对称分析研究了时间分数阶偏微分方程,例如,文献[8]对时间分数阶Harry-Dym方程进行李对称分析,并构造了方程的群不变解.文献[9-10]分别对时间分数阶Navier-Stokes方程组和Keller-Segel方程组进行李对称分析并构造出守恒律.还有一些学者利用李群分析对方程进行群分类,文献[11]对时间分数阶扩散方程进行群分类,并做相对应的对称约化得到方程的不变解.仅有少部分学者利用李对称分析研究时空分数阶偏微分方程,例如,文献[12]对时空分数阶Rosenou-Haynam方程进行了李对称分析,文献[13]对时空分数阶非线性演化方程进行了对称分析.

Noether定理建立了守恒律和对称之间的联系.文献[14]提出了一个新的守恒定理,即建立没有经典拉格朗日方程的微分方程的守恒定律.在此定理的基础上,文献[15]建立了时间分数阶微分方程的守恒律,文献[12]建立了时空分数阶Rosenou-Haynam方程的守恒律.本文将在李对称的基础上建立一类时空分数阶非线性方程的守恒律.

双多孔介质方程在物理、工程科学等方面有很多应用.文献[16]研究了整数阶双多孔介质方程的奇解和解的渐进行为.文献[17]用不变子空间方法对整数阶双多孔介质方程进行研究求解.文献[18]研究了具有非发散算子的双多孔介质方程的爆破和关键指数分析.文献[19]通过构造修正多孔介质方程的自相似解,研究了修正多孔介质方程的一族自相似解的存在性.文献[20]用李对称分析研究了时空分数阶多孔介质类型方程并利用李代数得到方程的群不变解.本文将利用李对称分析对一类形式简单的广义时空分数阶双多孔介质方程进行研究.广义的时空分数阶双多孔介质方程为

其中,(i=1,2,3)分别为关于t和x的分数阶Riemann-Liouville导数.u是关于x,t的未知函数,0＜α＜1,1＜βi＜2(i=1,2,3),0,b,c均为实数.

本文考虑方程(1)中b=c=0的情形,在这种情况下,方程(1)变为如下的时空分数阶非线性偏微分方程

特别地,当β=2时,方程(2)变为如下的时间分数阶非线性偏微分方程

本文将构造方程(2)和方程(3)所允许的李代数、一维优化系统和精确解,并对方程(2)的守恒律进行研究.本文结构如下:在第二节,介绍本篇文章所涉及的基础知识.在第三节,构造方程(2)和方程(3)所允许的李代数和相应的一维优化系统.在第四节,基于第三节得到的优化系统,对方程(2)和方程(3)进行对称约化并计算相应的群不变解,并用数学软件Matlab画出时空分数阶方程(2)的精确解的三维图.在第五节建立方程(2)的守恒律.在最后一节给出本文的总结.

2 基础知识

本节给出分数阶Riemann-Liouville导数的定义和李对称分析的步骤.

定义2.1设n∈N.则α阶Riemann-Liouville导数的定义为当0＜n-1＜α＜n时.其中为通常的n阶偏导数,为伽马函数.下面考虑一般的时空分数阶偏微分方程

假定单参数Lie群变换为

其中ηα,t,ηβ,x,ηxx的定义为

Dx和Dt是关于x和t的全导数且定义为

设方程(4)的无穷小生成子为

其中

无穷小生成子(8)所对应的向量场能生成方程(4)的一个对称当且仅当方程(4)的向量场V满足以下不变准则

延拓算子Pr(α,2)V定义为

其中ηα,t,ηβ,x,ηx和ηxx分别满足(6)式-(7)式.

此外,基于不变准则(10),时空分数阶偏微分方程(4)还需满足以下初始条件

引理2.1[5]设α＞0,0.当α+β＜1且2α+β＜1时,如下分数阶微分方程有精确解

3 李对称和一维优化系统

本节将利用对称分析方法计算出方程(2)和方程(3)所允许的李代数及相应的一维优化系统.

3.1 方程(2)的李对称和优化系统

本节利用对称分析法来推导方程(2)的李代数,再由李代数构造出方程(3)的一维优化系统.

定理3.1时空分数阶方程(2)的李代数l1由以下向量场张成

证明将方程(2)代入不变准则(10),可以得到方程(2)的不变方程为

将(6)式代入(14)式,并使方程中线性无关的u的各阶导数的系数等于零可以得到以下决定方程组

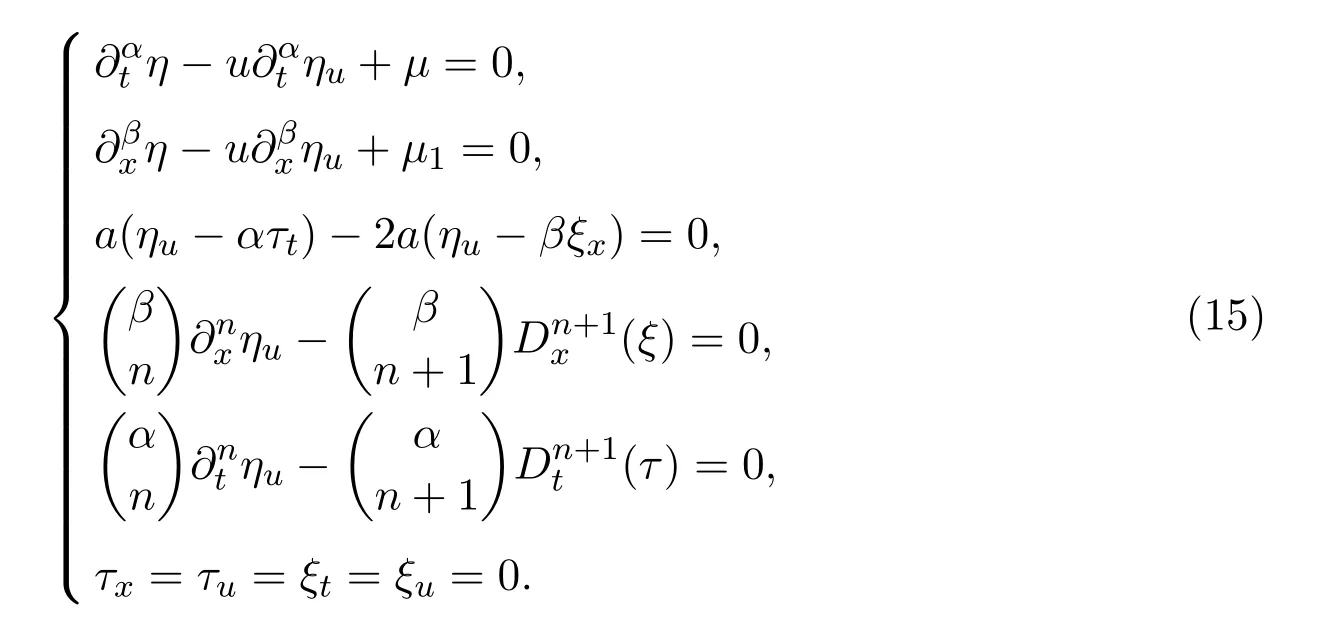
求解决定方程组(15)可得

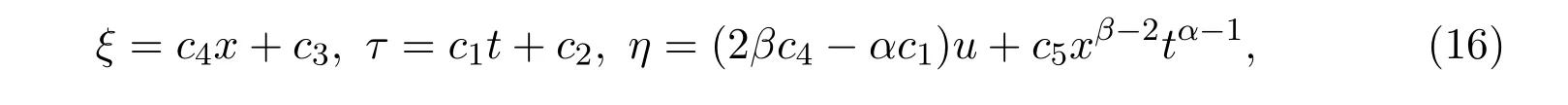
其中ci(i=1,2,3,4,5)是任意常数.根据不变条件(10)可以推出c2=c3=0.

由此可证方程(2)的对称群为(13).下面来计算李代数l1的一维优化系统.

通过计算得到李代数l1的非零交换子为

另外,伴随算子的作用由以下李级数给出

其中ϵ为任一参数.根据上式,能够推导出李群G1对李代数l1的伴随作用,如表1所示.按照文献[21]介绍的方法,可以得到李代数l1关于时空分数阶α,β的一维优化系统,结果在下述定理给出,这里省略其证明过程.

表1 向量场(15)的伴随表示

定理3.2(1)对于李代数l1的一维优化系统为

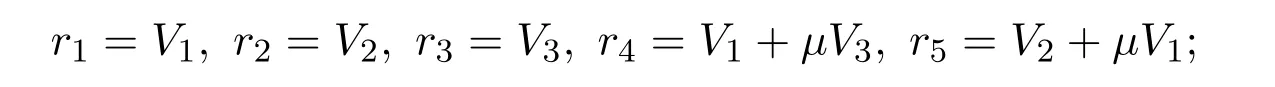
3.2 方程(3)的李对称和优化系统

本小节将利用对称分析构造方程(3)所允许的李代数和相应的一维优化系统.

定理3.3时间分数阶方程(3)的李代数l2由以下向量场张成

证明将方程(3)代入不变准则(10),可得

把(6)式代入(19)式,并令u的各阶线性无关导数的系数等于零,化简后可以得到以下决定方程组

求解决定方程组(20)可得

其中ci(i=1,2,3,4,5)是任意常数.此外,由初始条件(12)可以推出c2=c3=0,即证方程(3)的李代数(18).

容易看出向量场V1和V3是伸缩算子,V2是平移算子,李代数(18)的非零交换子为

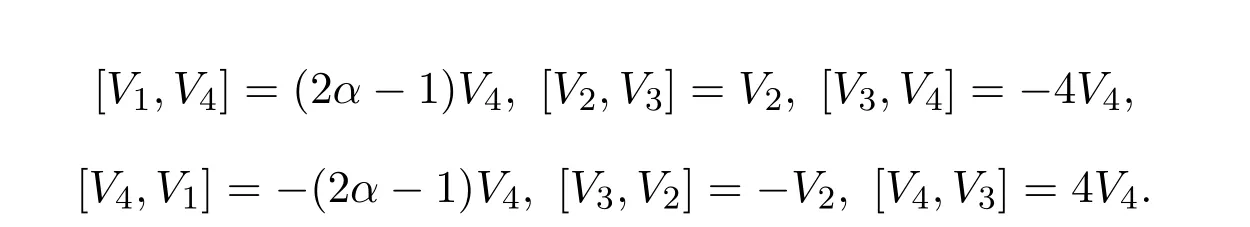
进一步地,由伴随算子的定义(17)可以推导出李群G2对李代数l2的伴随作用,如表2所示.

表2 向量场(17)的伴随表示

与前一小节类似,按照文献[21]介绍的方法可以得到以下定理.

定理3.4(1)对于和μ∈R,李代数l2的一维优化系统为

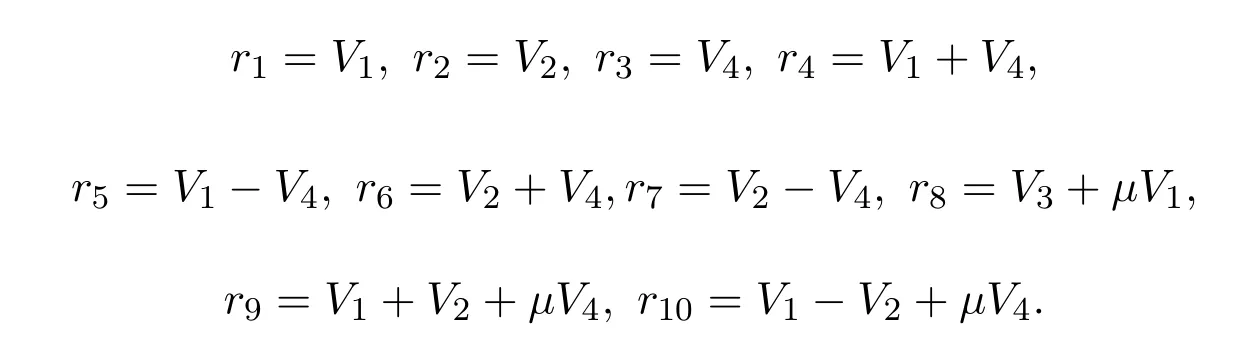
4 对称约化和群不变解

本节利用定理3.2和定理3.4所得到的结果,对方程(2)和方程(3)做对称约化并构造相应的群不变解,并给出群不变解的图像.

4.1 方程(2)的对称约化和群不变解

本小节利用定理3.2得到的一维优化系统,将复杂的非线性时空分数阶微分方程约化为较为简单的分数阶常微分方程,约化后的分数阶常微分方程将更容易求解.下面介绍定理3.2中一维优化系统对应的对称约化和群不变解.

对于方程(2)有以下情形成立.

情形1:r1=t∂t-αu∂u.对应的特征方程为

计算特征方程(22)可得方程(2)的两个不变量为x和utα,从而方程(2)有如下形式的群不变解

情形2:r2=x∂x+2βu∂u.对应特征方程为

计算方程(25)可知方程(2)有如下形式的群不变解

将(26)式代入方程(2)可得

将(27)式代回(26)式得到方程(2)的一个精确解为

对于(28)式,通过数学软件Matlab绘制如下图1三维图像解.

图1 u1(x,t)的三维图像.

在图1(a)和图1(b)中,取a=-1,β=1.5,可以观察到随着时间分数阶导数的阶数α的增大,u1(x,t)逐渐减小,当t趋于零时,曲率逐渐增大.在图1(c)和图1(d)中,取a=-1,α=0.4,可以观察到随着空间分数阶导数的阶数β的增大,u1(x,t)也增大,当x趋于零时,曲率逐渐减小.在图1(e)和图1(f)中,取α=0.3,β=1.5,可以观察到参数a对精确解u1(x,t)的影响.

4.2 方程(3)的对称约化和群不变解

本小节利用定理3.4中得到的一维优化系统,将复杂的非线性时间分数阶微分方程约化为较为简单的常微分方程,约化后的常微分方程更容易求解.下面介绍定理3.4中方程(3)的对称约化和群不变解.

对于方程(3)有以下情形成立.

情形1:r1=t∂t-αu∂u.r1对应特征方程为

计算特征方程(29)得方程(3)的群不变解为u(x,t)=t-αf(x),f(x)满足如下常微分方程(当时)

情形2:r2=∂x.计算r2对应特征方程得到群不变解为u(x,t)=g(t),代入方程(3)得到(t)=0,计算得到g(t)=ktα-1,其中k为任意常数.从而方程(3)的一个群不变解如下

情形3:r4,5=±∂x+t∂t-αu∂u.r4对应的特征方程如下

计算(31)式,得到方程(3)的一个群不变解为

其中f(z)(z=te∓x)满足如下分数阶常微分方程

情形4:r6,7=∂x±tα-1∂u.r6的特征方程为

解特征方程(32)可以得到方程(3)有如下群不变解

将(33)式代回方程(3)得g(t)=ktα-1.因此,方程(3)的精确解为

5 守恒律

本节在李代数(13)的基础上,建立时空分数阶方程(2)的守恒律.

方程(2)的守恒向量C=(Ct,Cx)满足如下守恒律

其中Ct=Ct(t,x,u,···),Cx=Cx(t,x,u,···).

方程(2)的拉格朗日形式如下

其中v(x,t)为新的因变量.欧拉-拉格朗日算子有如下形式

由(36)式可以得到方程(2)的伴随方程为

取v(x,t)=φ(x,t,u),得到如下方程

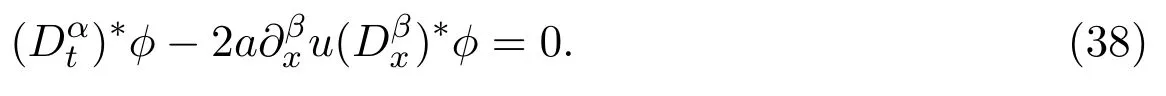
解(38)式得到

其中A为任意常数.

下面将通过以下公式分别建立守恒向量t,x的分量

其中n=[α]+1,m=[β]+1,Wi=ηi-ξiux-τiut,J,J1定义为

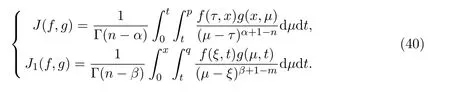
结合向量场(13),可以得到以下特征方程

取A=1,可以得到以下结论:

当0＜α＜1,1＜β＜2时,方程(2)的t分量的守恒向量为

当0＜β＜1,0＜α＜1时,方程(2)的x分量的守恒向量为

当1＜β＜2,0＜α＜1时,方程(2)的x分量的守恒向量为

6 结论

本文研究了李对称分析在时空分数阶微分方程的应用,并以一类广义时空分数阶双多孔介质方程为例,计算了它所允许的李代数并建立了优化系统.进一步地对方程(2)和方程(3)进行了对称约化,在此基础上得到方程(2)的精确解u0,u1,方程(3)的精确解u2,u3,u4,并用数学软件画出方程(2)的精确解u1(x,t)的三维图像.最后,利用定理3.1的结论和新Noether定理构造了方程(2)的守恒律.