顾鹏飞 李 刚

(江苏省扬州大学数学科学学院，225002)

圆锥曲线作为中学数学的重要内容,是历年各地高考的考查重点.以动直线为背景的圆锥曲线问题又是高考命题的热点,但从处理这类问题的表现上看,学生往往摸不清思路,导致事倍功半.究其原因,在解题过程中,学生难以回答“从何处下手”与“向何处前进”这两个最基本的问题[1].本文结合近几年的高考中出现的以动直线为背景的圆锥曲线题,浅谈笔者在处理这类问题时的观点,与同行交流.

一、由问题解法引出的思考

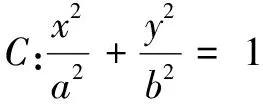
(1)求椭圆C的方程;

(2)设O为原点,直线l:y=kx+t(t≠±1)与椭圆C交于两个不同点P,Q,直线AP与x轴交于点M,直线AQ与x轴交于点N.若|OM||ON|=2,求证:直线l经过定点.

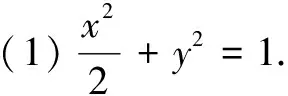
(2)解法1设而不求

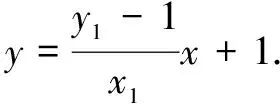
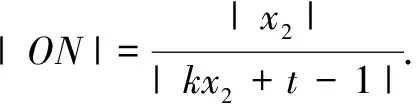
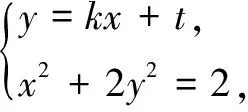
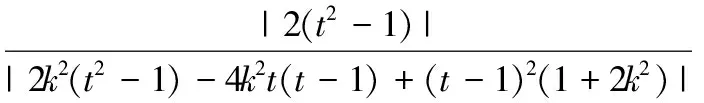
又因为|OM||ON|=2,所以t=0,即直线l经过定点(0,0).

解法2直接求

设直线AP的方程为y=k1x+1,AQ的方程为y=k2x+1.

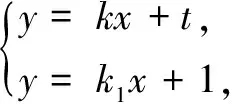
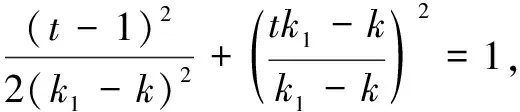
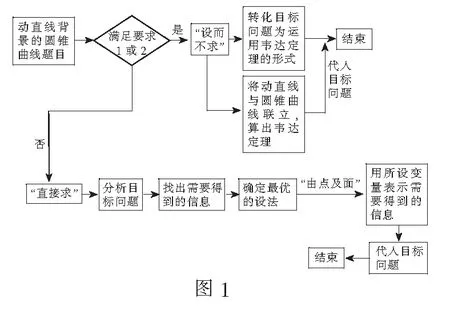
故k1,k2为(2t2-2)x2+(4k-4tk)x+(t-1)2=0的两个根,有

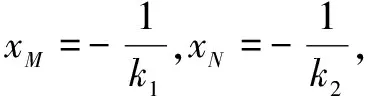
在处理圆锥曲线问题时,解题方法大致分为两类:“设而不求”与“直接求”[2].显然这道例题适应两种不同的解法,但本文主题并非探讨一题多解,而是通过对方法的比较,总结出这两种解法在不同问题中的优劣性.下面笔者将对这两种方法进行探讨.

二、两种方法的要点总结

“设而不求”的方法,是通过设动直线与圆锥曲线的两个交点,记为A(x1,y1),B(x2,y2),然后将动直线与圆锥曲线联立方程组,得到韦达定理的结果,再把目标问题的代数形式化简成便于运用韦达定理的形式.在解题过程中,设两个交点的坐标,但不求出任一交点坐标的具体形式,故此种解法称为“设而不求”.

“设而不求”的核心手段在于韦达定理,从韦达定理的形式x1+x2,x1x2(y1+y2,y1y2,x1y2+x2y1等皆是韦达定理的变形)知,x1与x2要保持某种对称性,这里的对称性指的是A与B两点的“地位”相同,即在题目中对A，B两点的操作相仿且在目标问题中代数式可转化为韦达定理的表达形式.在实际问题中,这两点要求通常是同时满足或同时不满足,故只需对其中一个要求进行判断即可.但值得注意的是,前者要求容易判断但主观性强,而后者略难判断但更客观,所以选择哪一个要求判断需要读者自己斟酌.值得一提的是,若通过前者确定了选用“设而不求”的方法,就可以引导学生将目标问题的代数形式转化成运用韦达定理的表达形式.

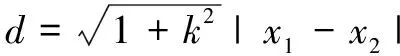
“设而不求”方法的意义不仅在于简化计算,而且能够让学生以全局的视角来思考数学问题,提升学生的逻辑推理核心素养.

“直接求”的方法,顾名思义,是先设未知数,然后通过联立圆锥曲线、利用题目所给条件等,将目标问题中的要求信息用所设的未知数表示出来的方法.“直接求”是一种解题线索较为清晰的“拼图式”方法,因为题中出现的重要的点和线可以通过所设未知数表示出来,故称为“直接求”方法.

“直接求”的核心思想在于由点及面,因为它是通过所设的未知数展开,利用题中条件来直接表示出各点与直线.值得注意的是,“直接求”方法的重中之重在于设未知数,因为题中的各个重要的点、直线等信息都将用这个未知数表示,同时所设未知数要尽量少,因为“多则生乱”,故未知数的选取决定计算量.

要确定最优的设法,必须从目标问题的角度考虑,由果溯因,从中找出需要得到的信息,然后比较哪一种设法能最快得出所要求的信息,使计算量降到最小.通常情况下,所设的未知数与动直线有关.

“直接求”方法的价值在于解题思路清晰,让学生反向出发,由果溯因,同时培养学生的数学运算核心素养.

综上,解决动直线背景下的圆锥曲线问题,运用“设而不求”或“直接求”的思路解题,其思维导图如下(注：其中的要求1：题目中对动直线与圆锥曲线的交点A，B的操作相仿；要求2：在目标问题中的代数式可转化为韦达定理的表达形式)：

三、应用举例与思路阐述

例2(2018年全国高考题题)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.

(1)当l与x轴垂直时,求直线BM的方程;

(2)证明:∠ABM=∠ABN.

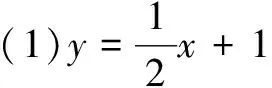
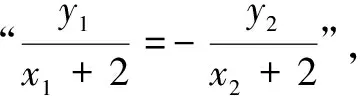
例3(2018年北京高考题)已知抛物线C:y2=2px经过点P(1,2).过点Q(0,1)的直线与抛物线C有两个不同的交点A,B,且直线PA交y轴于点M,直线PB交y轴于点N.

(1)求直线l的斜率的取值范围;

解析(1)(-∞,-3)∪(-3,0)∪(0,1)(过程略)

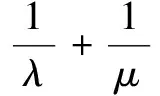
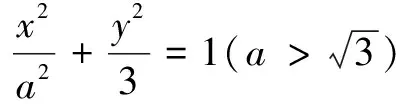
(1)求椭圆的方程;

(2)设过点A的直线l与椭圆交于点B(B不在x轴上),垂直于l的直线与l交于点M,与y轴交于点H.若BF⊥HF,且∠MOA≤∠MAO，求直线l的斜率取值范围.

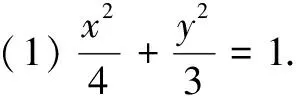
四、结论与建议

至此,本文介绍了以动直线为背景的圆锥曲线问题的解题策略,通过阅读题目，从巧妙设置变量、分析目标问题，双向出发,回答了“从何处下手”和“向何处前进”的问题.本文更像是一篇指导,引导学生的解题思路,避免陷入题海.因为数学解题杜绝拿笔就写,而是要先理解题目,思考题中条件与目标之间的内在联系.当然,若是作为压轴题出现的圆锥曲线问题,扎实的数学基础与清晰的解题思路缺一不可,如此才能在解题中游刃有余.