陈小燕

(福建省厦门大学附属实验中学，363123)

证明三点共线是几何问题中的热点，很多竞赛题都涉及到三点共线的问题.不少学生对这类问题感到困惑和棘手,不知道从何处入手.本文以2022年福建省的一道竞赛题为例,从不同视角给出多种解法，为同学们在今后遇到此类问题时提供一定的参考.

试题(2022年福建省青少年数学水平测试题)如图1,四边形ABCD是平行四边形,∠DAC=45°,以线段AC为直径的圆与AB和AD的延长线分别交于点E和F,过点B作AC的垂线,垂足为H.求证:E,H,F三点共线.

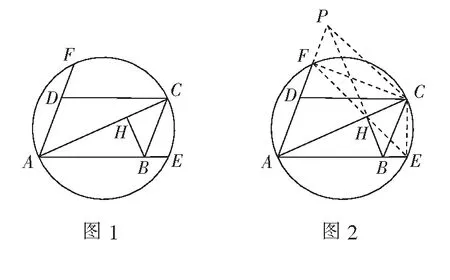
视角1利用邻角互补

连结CE,CF,要证E,H,F三点共线,只要证∠CHE+∠CHF=180°.

证法1如图2,延长BH交直线AD于点P,连结CP.因为∠DAC=45°,BP⊥AC,所以∠BPA=45°.

又由四边形ABCD是平行四边形,可得∠BCA=∠DAC=45°,所以有∠BPA=∠BCA.于是P,A,B,C四点共圆,得

∠CBE=∠APC.

①

连结CE.由AC为圆的直径,得∠CEA=90°=∠CHB,所以C,E,B,H四点共圆,可得

∠CHE=∠CBE.

②

连结CF.由AC为圆直径,得∠CFP=90°=∠CHP,所以C,H,F,P四点共圆,可得

∠APC=180°-∠CHF.

③

综合上述①②③ 三式,可得到∠CHE=∠CBE=∠APC=180°-∠CHF,即∠CHE+∠CHF=180°.所以E,H,F三点共线.

视角2利用西姆松定理

延长BH交直线AD于点P,连结CF,CE,易见CF⊥AP,CE⊥AB,CH⊥PB.由西姆松定理,要证E,H,F三点共线,只要证A,B,C,P四点共圆.

证法2如图3,延长BH交直线AD于点P,连结CF,CE.因为∠DAC=45°,BP⊥AC,所以∠APH=45°.

又因为四边形ABCD是平行四边形,所以∠ACB=∠DAC=45°=∠APH,可得A,B,C,P四点共圆.

因为AC为圆的直径,所以CF⊥AP,CE⊥AB.又因为CH⊥PB,由西姆松定理,得E,H,F三点共线.

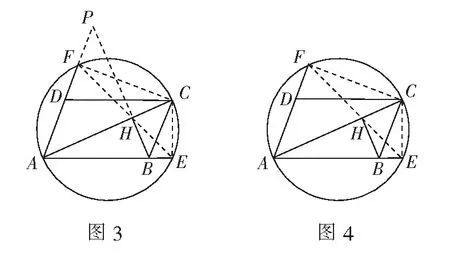
视角3利用两角重合

连结CE,CF,EF,要证E,H,F三点共线,只要证∠FEC=∠HEC.

证法3如图4,连结FC,CE,HE,FE.因为四边形ABCD是平行四边形,所以∠ACB=∠DAC=45°.

因为AC为圆的直径,所以CF⊥AF,CE⊥AB.又因为BH⊥AC,所以C,E,B,H四点共圆.于是∠HEC=∠HBC=90°-∠ACB=45°.

因为F,A,E,C四点共圆,所以∠FEC=∠FAC=45°.所以∠FEC=∠HEC,可得E,H,F三点共线.

视角4同一法

如图5，连结FH并延长交题设圆于点G.要证E,H,F三点共线,只要证点G与E重合.

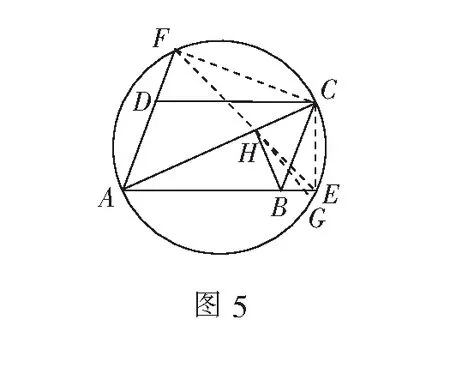
证法4连结FC,EC,延长FH交题设圆于点G.

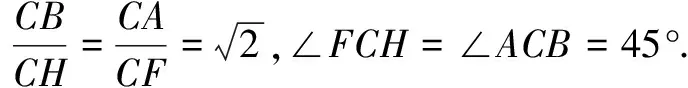
所以∆CFH∽∆CAB.

综上,E,H,F三点共线.

综上可见,求解三点共线问题的方法灵活多样,结我们的解题留下了广阔的思维空间.对于此类问题的解法进行探究,有助于加强几何不同模块有关知识的联系,多角度探究问题的求解途径,不断培养解题能力,提升数学素养.