程凯杰

（北京邮电大学理学院，北京 100876）

0 引言

索膜结构具有自身重量轻、曲面结构造型优美、结构效率高的优点，并且能够跨越较大的空间。索膜结构经过近几十年的发展，已经被广泛应用于体育娱乐设施、公共景观建筑等大型建筑中[1]。在索膜结构设计中，我们通常最关心同时研究最多的问题就是索膜结构的形状确定问题，即找形问题。目前找形分析在分析确定索膜结构形状时常用到以下几种数值分析方法：非线性有限元法、动力松弛法和力密度法。这三种找形方法虽然具体做法步骤不同，但都是需要先建立刚度方程，再利用迭代法或直接法，对方程进行求解。其中力密度法在找形过程中将几何非线性问题转换成线性问题，避免了非线性系统的收敛问题，与上述另外两种找形方法相比具有较快的计算速度。

力密度法找形[2]是目前最常使用的找形方法之一。使用力密度法找形通常需要先将索膜结构离散成由单元和节点构成的网状模型，然后通过设定力密度值并依据结构中单元和节点之间的拓朴关系，建立关于所有节点的平衡方程组，即力密度方程组，最后通过求解力密度方程组得到各节点的坐标，从而确定结构的曲面形态[2]。力密度方程组的求解问题本质上依然是线性方程组的求解问题。

由于力密度方程组的系数矩阵是大型的稀疏矩阵，如果运用直接解法求解力密度方程组，效率不高甚至难以实现。高振宇在2012 年发表的求解力密度方程组的优化算法[3]中，基于力密度方程组系数矩阵正定、对称、稀疏的结构特点，将迭代解法中的共轭梯度法运用到力密度方程组的求解中，文献[3]中的算法具有收敛快、精度高的优点，可以有效的解决力密度方程组的求解问题。然而随着结构单元和节点数目的指数增长，我们在使用经典算法在求解大型稀疏的力密度方程组时需要大量的计算时间和存储空间。

量子计算作为一种新发展起来的计算模型，在解决一些困难的计算问题中产生了颠覆性的影响。2008 年，Harrow 等[4]研究并提出了HHL 算法：输入一个log2n 位的量子态│b〉=Σbi│i〉，运用哈密顿模拟在常数时间内实现酉变换e-iAt，那么算法可以在对数时间内得到一个满足线性方程Ax=b 的量子态│x〉=Σxi│i〉。HHL 算法为大型稀疏线性方程组的求解问题带来了突破性的进展。我们在本文中将量子计算求解线性方程组的技巧运用到力密度方程组的求解中，研究并提出求解力密度方程组的量子算法，与经典算法相比，我们的算法具有良好的指数加速效果。

1 力密度法找形

力密度法[2]最早是由H.J.Schek 在1974 年提出用于索膜结构的找形方法，后来经过学者们的完善和发展，如今已经成为索膜结构中解决形状确定问题的主要方法。它的具体步骤是：先将索膜结构离散成单元和节点的网络模型，然后通过设定力密度值并根据结构单元和节点之间的拓朴关系，建立关于所有节点的平衡方程组，即力密度方程组，最后通过求解力密度方程组得到各节点的坐标，从而确定结构的形状。在笛卡尔坐标系中xj（j=1，2，3），将索膜结构离散为由m 个单元n 个节点组成的网络模型。考虑结构中任意节点i（i=1，2，…，n）在xj方向的平衡条件为：

在力密度法中，我们通常定义qik=Nik/Lik为单元ik的力密度，那么式（1）可以写成：

接着我们可以对所有n 个节点建立与式（2）相同的平衡方程，并将其表达成矩阵的形式为：

式中：I（t）——单元的首节点；K（t）——单元的末节点。Xj（j=1，2，3）是一个n 维的列向量，其中的元素为节点i（i=1，2，…，n）在方向xj（j=1，2，3）上的坐标，Fj也是一个n 维列向量，它的元素为作用在节点i（i=1，2，…，n）上的荷载在方向xj（j=1，2，3）上的分量。综合上面所有描述可以得知，我们通过求解式（3）的矩阵方程即可得到节点（i=1，2，…，n）在方向xj（j=1，2，3）上的坐标，从而确定模型的初始形状。

2 用量子计算求解矩阵方程CTQCXj=Fj

本节主要介绍了求解力密度方程组的量子算法。研究并利用了力密度方程组系数矩阵的特点，发现系数矩阵是个大型稀疏实对称矩阵，接着对力密度方程组的系数矩阵进行分解，将分解后的系数矩阵扩展到一个更高维的Hilbert 空间中，在求解线性方程组的量子算法的基础上，设计量子算法对力密度方程组进行求解。在求解力密度方程组中使用HHL 算法需要用到哈密顿模拟技术，将力密度方程组的系数矩阵（CTQC）指数化，哈密顿模拟的前提条件是能通过黑盒读取访问矩阵的元素。矩阵方程CTQCXj=Fj的系数矩阵（CTQC）不仅是稀疏矩阵，还具有对称、正定的特性[3]，满足HHL算法对于方程系数矩阵稀疏性的要求，但是系数矩阵（CTQC）的模拟涉及矩阵的乘法，需要进行大量的计算，因此，为了防止破坏量子计算的加速效果，本文先对系数矩阵进行如下操作：

那么矩阵方程CTQCXj=Fj可以写成CTQ′Q′CXj=Fj，由于Q′是对角矩阵，所以：

记A=Q′C，那么有：

式（7）的解可以表示为：

由HHL 算法可知，为了不失一般性，我们需要假设：

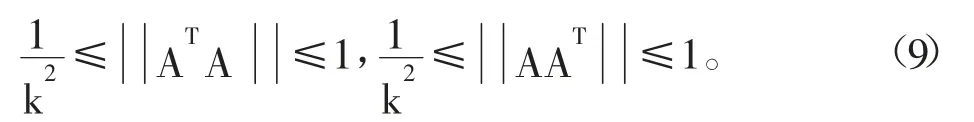
由于HHL 算法中哈密顿模拟要求矩阵是厄密的，矩阵Am×n是一个矩形矩阵并不是厄密矩阵，不满足哈密顿模拟的前提条件，我们在设计算法时需要将求解ATAXj=Fj转化为系数矩阵厄密的情形。所以我们设计一个变换I，利用I 将矩阵A 和AT表示成Cm+n上的厄密矩阵。I 作用到矩阵A 上有以下效果：

那么我们可以将式（6）改写成：

式（1）的解为：

具体的算法过程如下：

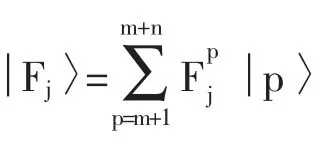
第二步，对矩阵I（A）进行哈密顿模拟得到eiI（A）t=Σkeiλkt│μk〉〈μk│；

第三步，执行相位估计，得到Σk│λk〉│μk〉〈μk│；

3 复杂度分析

而经典算法求解力密度方程组所需的时间一般介于O（n1.6）和O（n1.7）之间，可见在求解力密度方程组时引进量子算法可以在时间上获得指数加速。

4 结语

力密度方程组作为索膜结构力密度找形的基础方程，它的求解是力密度法找形中最后也是最主要的一步，本文应用量子计算的思想和方法求解力密度方程组，通过对力密度方程组的系数矩阵进行分解、引入映射算子等操作，使力密度方程组满足HHL 算法的量子模型，从而求得其解，与经典算法相比，具有指数加速。另外，本文的方法得到的是解的量子态形式，可以通过量子层析的方法进一步获得解的全部经典信息。能否使用量子算法直接对系数矩阵进行模拟，并在求解力密度方程组中获得加速效果还需要后续的研究。