裘迪波 王孙君

[摘  要] “运算定律”单元学习的是运算体系中具有普遍意义的规律，其中乘法分配律是学习的难点。为让学生在大概念的统摄下，系统学习加减乘除中的三大定律，突破难点，在梳理前期学习内容、调研生情的基础上，对本单元学习内容进行了适度整合与实践。借助“重构模型化数学知识，培养凑整性简算意识，感受数学思考价值”等策略，助推学生系统建模，发展学力，培养学生的高阶思维能力。

[关键词] 运算定律;梳理分析;整合重构;发展学力

“运算定律”（人教版四年级下册第三单元）编排了两节内容：先学习加法运算定律及其应用，内含连减的简便计算;再学习乘法运算定律及其应用，练习中包括连除的应用。教材共安排了8个例题和2个专项练习。笔者用心研读本单元教材的编排体系，结合多年的教学经验，觉得看似清晰、系统的知识脉络似有碎片化之感，而且每个定律平均用力，难点无法突破。为此，引发了笔者思考，笔者在梳理前期学习内容、调研生情的基础上，对本单元学习内容进行了适度整合与实践。

[?]一、笔者的思考

1. 能否建立“运算定律”大概念统摄教学

运算定律是数的运算体系中具有普遍意义的规律，如果将“运算律”作为大概念，那么交换律、结合律、分配律都从属于它。在运算定律大概念统摄下，我们是否可以探索加减乘除运算中，哪些数的运算存在着交换律、结合律、分配律？能否从大概念角度进行系统教学？

2. 如何突破“乘法分配律”這一核心定律

三个乘法运算定律中，乘法分配律是学生最难理解的，也是数的运算中应用最广泛、最能体现简算性的运算定律，教材编排了例7作为一课时进行教学。如何才能突破这一难点，让学生真正理解乘法分配律的内涵，并能正确地拓展应用？

3. 怎样结合“问题解决”锤炼简算意识

教材注重运算定律与简便计算技巧的训练，采用“一例一练”的方式对应编排。如何很好地将运算定律的学习和解决生活中的实际问题相结合，从而更好地培养学生的“简算意识”？

[?]二、前置内容梳理和学情分析

（一）教材内容，前有孕伏

通过梳理前面七册教学内容，笔者发现：一上一图四式和二上乘法口诀对交换律有了提前渗透，三上、三下和四上通过学习多位数乘法初步体会乘法分配律、结合律以及相关的连乘、连除性质。教材整体编排对加法、乘法运算定律有了一定的孕伏。

（二）学情调测，提供依据

1. 前测分析

笔者对城区、城郊和乡镇三个层面的四年级6个班学生进行了学情前测，从学生认知结构、知识结构两方面进行了调查统计。

分析统计结果，笔者发现：1、2题各层面的正确率达到了80%左右，3题各层面的正确率在50%及以下，说明学生对加法交换律和乘法交换律在认知上有了一定的感知。但大部分学生不能用文字或图画来表示，说明学生对交换律的内涵不是很清楚，比较模糊。4、5两题各层面的正确率在23%和38%之间，说明大部分学生对减法和除法是否有交换律存在疑惑，学生的认知结构还缺乏完整性。

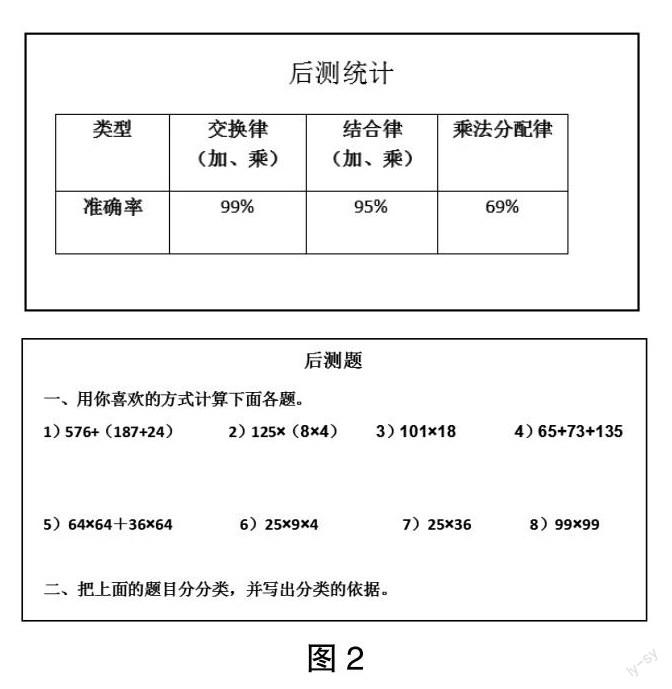
2. 后测分析

在对四年级学生进行前测的基础上，笔者还对城区五年级学生进行了后测统计（主要从学生对知识的理解、应用意识上进行了统计）：

分析发现：学生对加法、乘法的交换律、结合律掌握得比较好，应用定律进行简便计算正确率很高;而乘法分配律的答题情况不容乐观，还有近30%的学生没有掌握，不能正确应用;学生的凑整应用意识不是很强。

[?]三、单元文本的整合尝试

在潜心研读分析教材编排和学生前后测学情的基础上，笔者对这单元内容进行了适当整合并确定了单元整体教学目标。

（一）研析学情，精准定位

1. 适当整合，突出大概念，系统呈现

在“运算定律”大概念统摄下，笔者将内容相似、结构相同的加法交换律和乘法交换律整合成一节交换律，把加法结合律和乘法结合律整合成一节结合律，把减法的简便运算和连除的简便运算整合成一节减法和除法的性质，在此之后安排一节交换律、结合律性质的综合应用。从学生的后测情况来看，学生对乘法分配律的应用掌握不够，所以笔者把乘法分配律分成两节课加以突破：分别为意义的理解和应用拓展两课时，最后为单元复习。运算定律的应用、解决问题策略多样化等分解在定律的应用拓展以及单元复习课中。具体框架如下：

这样整合，更有利于学生感悟知识之间的联系与区别，完善学生的认知结构，同时突破模型结构相对复杂的乘法分配律。

2. 延长课时，突破难点，建构模型

乘法分配律具有高度的抽象性和概括性，其模型结构对学生来说很难建立。教材只安排了一个例题一课时来学习，大部分学生难以理解。笔者应拉长学习时空，拉长乘法分配律的建构过程，设计贴近生活的问题情境，充分展示思维过程来保证模型的建构，让学生在经历“猜想→验证→归纳→建模”中真正理解定律的内核，培养学生高层次的数学思维能力。

3. 夯实基础，灵活应用，锤炼意识

常态教学中，教师往往偏向简便计算能力的训练，忽视学生凑整意识的培养。容易造成学生看题目要求简便计算，就进行简算;一旦没有这个要求，就按常规方法计算。因此，笔者应按照“前有孕伏，提前渗透;中有突破，灵活简算;后有发展，锤炼意识”的整体性教学思路，有的放矢地锤炼学生的简算意识。

（二）呈现价值，制定目标

为了突出单元整体性，笔者预设了“强化意义、锤炼思维、体现价值”的单元目标：

1. 强化运算定律意义的理解，建构“模型化”数学知识

让95%以上的学生能识别和理解运算定律和性质;85%以上的学生能选择合适的算法模型，灵活运用;70%以上的学生会运用模型，创编合适情境。

2. 提升运算定律应用的能力，培养“凑整”简算意识

运算定律教学不能简单等同于简便计算教学，运用运算定律进行简便运算的本质是凑整，培养学生凑整的简算意识。

3. 不断积累基本活动经验和思考经验，培养学生的高阶思维能力

让学生经历观察、发现、猜想、举例、验证、归纳等思考过程，感受数学思考的价值，培养学生的高阶思维能力。

[?]四、单元整合教学实施策略

为实现上述目标，笔者借助重构“模型化”数学知识，培养“凑整”简算意识，感受“数学思考”价值等策略，帮助学生重构建模、发展学力。

（一）数形交融，建构“模型化”数学知识

1. 以形促数，丰富活动经验

教学定律时，笔者借助图形表征，丰富学生的活动经验，促使学生理解内化。如教学交换律时，看图算一算：★★★  ★★★★ 一共有多少个五角星？●●●●● ●●●●一共有多少个圆？借助计算图形个数，得出3+4=4+3，5+4=4+5。这样让学生体会形中有数，以形促数，使学生更加深刻地理解运算定律的意义。

2. 形中思数，强化运算本质

乘法分配律的理解和应用是本单元教学的难点。笔者借助图形表征、符号表征等不同方式来促进学生理解定律的本质。如让学生计算长方形的面积（如图4），有的学生用101×50，有的用100×50+1×50。

101×50 100×50+1×50

=（100+1）×50 =5000+50

=100×50+1×50 =5050

=5000+50

=5050

通過两种方法计算面积，让学生“形中思数”，借助图形的直观性将抽象的运算定律形象化、简单化，让学生运用多种感官充分感知，搭建数与形之间的桥梁，学生对“以形思数”的感悟会有更高层次的理解，从而强化运算定律的本质。

3. 数形互补，构建数学模型

笔者还尝试借助图形来进行乘法分配律的教学（如图5：妈妈各买了3盒两种规格的口罩，妈妈总共买了多少个口罩？）让学生结合点子图表述所写算式（5+7）×3=5×3+7×3的含义。

这样借助图形从分到合或从合到分进行动态展示，巧用图形表征给学生一个“理解的支点”，一方面借助图形可以探索出运算定律，体现“数中有形”;另一方面利用图形呈现的多样性，可以发现数的运算规律，体现“形中有数”。这样一种教学方式让学生真正感受到数形结合的魅力。数形互补，促使学生主动建构乘法分配律。

（二）一题巧用，培养“凑整性”简算意识

1. 一题多解，锤炼简算技能

如计算50+25×88，引导学生用不同的方法解决：50+25×（80+8），50+25×4×22，50+25×8×11，25×2+25×88=25×（2+88），既应用了乘法分配律，又涉及了乘法结合律。通过一题多解，灵活简算，锤炼学生的简算技能。

2. 一题多变，激活简算意识

如在复习运算定律时设计下题：

25×43_______，在横线上填写数与运算符号，使式子能简便计算。

这题会呈现多种结果，如25×43×4、25×43+25×57等，既有应用乘法交换律、乘法结合律的简算，又有应用乘法分配律的简算。这样的一题多变，可激活学生的简算意识和简算思维。

3. 一题多编，灵活简算应用

如教学单元综合应用时，让学生选取125、32、68、8、101中的任意几个数，编写一个能简便计算的式子，并说明用什么定律或性质。学生可能会编出：125×32=125×8×4，68×101=68×1+68×100，等等。在经历自主编题、思考的过程中，进一步锤炼了学生的简算意识和运算技能。

（三）积累经验，感受“数学思考”的价值

运算定律的学习过程是后续代数知识学习的基础，也是后续学生灵活处理计算问题积累相应活动经验的过程。因此，教学时要尽可能拉长、凸显这个过程，让学生在不断经历数学活动的过程中积累经验，感受数学思考的价值。

1. 从“探究尝试”走向“猜想验证”

如学习交换律时，当学生通过观察引发猜想、自主验证，发现并归纳出加法交换律后，教师追问“加法中有交换律，其他运算中是否也存在着这样的定律呢？”由此引导学生从加法迁移到四则运算，让学生再次提出猜想：有的说乘法中可能也有交换律，有的认为减法和除法中可能也有交换律。然后根据学习单让学生自主举例验证，交流反馈，得出结论。两次猜想、验证，进一步锤炼了学生的思考能力和学习能力，促使学生的思维从低阶步入高阶。

2. 从“归纳建模”走向“数学应用”

如探究乘法分配律时，笔者设计了以下四个练习：

（1）在○里填上<、>或=。

（4+2）×25○4×25+2×25，8×（125+25）○8×125+8×25。

（2）请再举几个这样相等的例子。

（3）请用字母表示上述相等的式子。

（a+b）×c=___×___+___×___，a×（b+c）=____×____+____×____。

（4）用乘法分配律计算：125×（8+4），64×64+36×64。

笔者先让学生判断左右两边的式子是否相等，再根据等式两边的变化过程，归纳建模，用字母表示出定律，最后应用定律进行简算。一步步引导学生从数到符号，从直观到抽象，从归纳到应用，推动着学生思维向纵深发展。

这样的单元整合学习，学生经历了一次次深入的探究活动，建构了一个个运算定律模型，深度学习在探究验证、重构建模中真实地发生着。