刘娜娜，王 昌

（西北大学 科学史高等研究院，陕西 西安 710127）

拓扑学被认为是现代数学的三大基础课程之一，欧拉示性数作为一个重要的拓扑不变量，与数学的许多分支均有广泛联系，陈省身先生曾在国际微分几何大会上说过：“欧拉示性数是大量几何课题的源泉和出发点。”[1]他将欧拉示性数与组合拓扑、椭圆拓扑、总曲率、同调、层的上同调和示性类联系在一起，其中涉及到现代数学中许多重要的公式和定理。如高斯-博内公式、欧拉-庞加莱示性数、阿蒂亚-辛格指标定理、霍奇指标定理、黎曼-罗赫定理、德拉姆同构定理等等，这反映出欧拉示性数在当代数学中的重要性。由于欧拉示性数最初的形式是欧拉多面体公式，因此，对欧拉多面体公式进行深入细致的研究，可以使我们更清楚地理解欧拉示性数的历史演变过程。

欧拉多面体公式，可以理解为多面体的拓扑特性，关于凸多面体的顶点数V、棱数E、面数F不变的关系：V-E+F=2，是欧拉（Leonhard Euler，1707—1783）在1750 年与哥德巴赫（Christian Goldbach，1690—1764）的通信中提及的。[2]478-480随后，欧拉写了两篇关于多面体的文章，都发表于1758 年。第一篇文章写于1751 年，是有关多面体公式的陈述。第二篇文章写于1752年，包含了对多面体公式的证明。[3-4]在发表了这两篇文章之后，他再也没有回到多面体这个话题。

后来的研究发现，欧拉多面体公式的这种不变性质对闭曲面、拓扑空间和高维流形等对象也有拓扑意义，现统称为欧拉示性数。19世纪下半叶，拓扑学逐渐在若尔当（Camille Jordan，1838—1921）、黎曼（Georg Friedrich Bernhard Riemann，1826—1866）、莫比乌斯（August Ferdinand Möbius，1790—1868）、克莱因（Felix Christian Klein，1849—1925）、贝蒂（Enrico Betti，1823—1892）、戴 克（Walther Franz Anton von Dyck，1856—1934）等人的工作中形成。庞加莱（Jules Henri Poincaré，1854—1912）在他一系列拓扑论文中，[5-11]揭示了代数拓扑的蓝图，并给出了欧拉多面体公式的第一个真正现代意义的解释——交错和，现在被称为欧拉-庞加莱示性数，是最基本的拓扑不变量之一。

V-E+F=2，这个看似简单的公式，却能够推广并应用到数学的许多不同分支，由此我们可以看到欧拉的工作及其重要影响。关于欧拉多面体公式的历史，国内外数学史家有过相关论述，主要的关注点在于对这段历史的核心人物欧拉和多面体公式的阐述，虽有一些论文介绍欧拉的多面体公式，但都未从原始文献出发阐述欧拉引入多面体公式的动机。[12-20]有鉴于此，本文通过分析欧拉有关多面体的原始文献，以及笛卡尔（René Descartes，1596—1650）的部分手稿，结合开普勒（Johannes Kepler，1571—1630）的《世界的和谐》相关章节，在“为什么数学”的研究范式下，[21]提出并回答这样的一个问题：欧拉为什么引入多面体公式？

1 对多面体的研究

早在希腊和文艺复兴时期，人们对多面体就有一定的研究。[17-20]毕达哥拉斯（Pythagoras，约前580—前500）、柏拉图（Plato，前427—前347）、欧几里得（Euclid，约前330—前275）和阿基米德（Archimedes，前287—前212），他们都曾痴迷于多面体。开普勒用柏拉图体建立了太阳系的早期模型。

尽管从未明确指出，但毕达哥拉斯等人假设的多面体都是凸的，即满足多面体的任何两点都可以由其内部的直线段连接起来。也就是说，不允许多面体有凹痕。对于我们接下来讨论的对象，我们假设：（1）多面体是凸多面体；（2）空心和实心都可以。

关于多面体，最早的发现应该是柏拉图体，也就是正多面体，即满足每个面是正多边形，所有的面全等且每个顶点有相同数量的面。希腊人对正多面体的理论最后主要的贡献要归功于阿基米德。根据帕普斯相关论述（Pappus，290—350），[22]阿基米德提出了半正多面体，现称为阿基米德体。和柏拉图体类似，阿基米德体应满足每个面是正多边形，允许不止一种类型的正多边形。随着希腊文明的衰落，数学活动中心的转移，直到中世纪的欧洲才重新开始对多面体进行研究。

1596年，开普勒的太阳系模型出现在他的《宇宙的奥秘》中，认为太阳系模型与柏拉图体的嵌套有关系。此外，在《世界的和谐》中，开普勒还对正多面体做出了新观察：

然而，在这些立体中存在着两组值得注意的不同等级之间的结合：雄性一方是初级形体中的立方体和十二面体，雌性一方则是次级形体中的八面体和二十面体，除此以外，还要加上一个独身者或雌雄同体，即四面体，因为它可以内接于自身，就像雌性立体可以内接于雄性立体，仿佛隶属于它一样。雌性立体所具有的象征与雄性象征相反，前者是面，后者是角。此外，正像四面体是雄性的立方体的一部分。宛如其内脏和肋骨一样，从另一种方式来看，雌性的八面体也是四面体的一部分和体内成分：因此，四面体是该组结合的中介。[23]3-4

开普勒对柏拉图体给出了一个重要的新发现，即正八面体与正六面体之间存在反对称关系（antisymmetric relationship），正二十面体与正十二面体之间存在反对称关系，正四面体存在对称关系。

如图1，正八面体与正六面体是反对称关系。正六面体的每一个面对应于正八面体的每一个顶点，因此，正六面体的面数等于正八面体的顶点数。正八面体的每一条棱都可以与正六面体的一条棱相对应，因此，这两个多面体必须具有相同的棱数。此外，正六面体的每一个顶点对应于正八面体的每一个面，因此正六面体的顶点数等于正八面体的面数。这样，我们就可以找到上述的反对称关系。类似的，开普勒说明了正二十面体和正十二面体也是反对称关系，正四面体是自对称的。此外，开普勒将这些正多面体赋予性别——正六面体和正十二面体是雄性，正八面体和正二十面体是雌性，而正四面体是雌雄同体的。

图1 开普勒《世界的和谐》插图

通过对上述引文的解读，我们可以看出——开普勒对不同正多面体的顶点数、棱数和面数作了比较和归类，并应用于他的宇宙模型中。无论是古希腊的柏拉图体和阿基米德体，还是开普勒的多面体宇宙，他们都想进一步了解多面体，观察多面体的特性，认识其规律性。

2 笛卡尔的工作

笛卡尔利用初等几何的观点对多面体进行研究，他几乎得到了我们现在数学上的多面体公式V-E+F=2，也有人称之为“笛卡尔失去的定理”。我们从笛卡尔在多面体的工作中可以看出，初等几何影响了拓扑学。下面将从莱布尼的手稿出发，详细解读笛卡尔在多面体的工作，分析其数学思想。

2.1 关于多面体的研究

1860 年，在欧拉提出多面体公式的一个多世纪之后，有证据表明，笛卡尔在1630年就知道这种多面体的关系，比欧拉早一百多年。笛卡尔有一部拉丁文著作出现在莱布尼茨（Gottfried Wilhelm Leibniz，1646—1716）的一个抄件中，现存于汉诺威（Hanover）的一个图书馆里。[24]

笛卡尔在他的手稿中提供了许多关于多面体的性质，他还可能给出了柏拉图体不超过5个的第一个代数证明。与欧拉多面体公式有直接联系的是有关平面角P的表达式：P=2F+2V-4。为了更好地理解笛卡尔的工作，需要两个概念——平面角和立体角。平面角是在一个平面内两直线相交的倾斜角；立体角是不在同一平面内多于两条线且相交于一点的线构成的立体图形。下面我们将对笛卡尔的手稿进行详细解读。

对笛卡尔的平面角公式重要的一个命题是多面体外立体角和，他是这样描述的：

正如在一个平面图形中，所有外角加在一起等于4个直角。所以在一个立体中，所有的外角加在一起等于8 个直角。构成立体角的所有平面角之和小于构成平面的4个直角部分，称为外立体角。[24]44

笛卡尔用“平面图形”代表“多边形”，我们用“立体”代表“多面体”，“一个直角”代表90o。很明显，笛卡尔是通过与多边形的类比推理发现，多边形外角之和等于4个直角（4△），那么对于多面体来说所有外角加在一起等于8 个直角（8△）。笛卡尔继续写道：

在四面体中，面数总是和立体角数一样多。在棱柱中，立体角数的一半比面数少2。在八面体中，面数的一半比立体角数少2。在其他立体中，人们可以想象更多的立体，一个立体中的平面角至少是立体角的3倍，如果一个立体中的立体角数减去2，然后将余数乘以2，则面数是最多的。但是把立体角数除以2，如果这个数是偶数，要加1，如果不是，把得到的商加2，则面数是最少的。面数和立体角之间存在很大的关系。[24]50

前三句是关于多面体的类型——四面体、棱柱、八面体，其面数和立体角数有特定的关系。第四句话指的是其他类型的多面体，他们的面数和立体角数之间也有特定的关系。显然，笛卡尔的动机是通过和多边形进行类比，因为多面体的面数和立体角数是多边形的边和角的推广。但是由于多面体的面数和立体角数之间没有特定的关系，所以他只能给出一些特殊类型的关系。

此外，笛卡尔还给出了关于多面体特征的一些不等式：比如立体各面的平面角之和等于立体角数的4 倍减8，即=4V-8；面数和立体角数的两个不等式：V≥+2，F≥+2；以及平面角数与面数、平面角和的关系：P=，等等，其中Σ表示所有平面角之和。

2.2 与多面体公式有关的内容

接下来，笛卡尔开始考虑多面体的顶点数，面数和平面角数的关系：

我经常把α表示立体角数，用φ表示面数，所有平面角的总和是4α-8，如果计算立体的面数与所有的面是三角形立体相同，则φ=2α-4。通过计算两个直角三分之一的角度，平面角数是6α-12。……平面角的实际数量是2φ+2α-4，这个不能超过6α-12，但如果少了，超出的就是4α-8-2φ。[24]54

现在对上述引文进行进一步的解读，我们用V表示立体角数，F表示面数；P表示平面角数以及Σ表示所有平面角之和。

这些结论显然是通过多边形相应命题类比提出的。通过类比多边形中边和角的关系，笛卡尔试图发现立体角数和面数之间的关系。笛卡尔计算多面体的特征，并在他们之间建立代数联系，可以推出平面角P的表达式：P=2F+2V-4。

正是因为笛卡尔发现了这个关系式，有学者认为欧拉多面体公式应该以笛卡尔命名。[24]从某种程度上说，笛卡尔的平面角表达式和欧拉的多面体公式是等价的。因为：如果多面体的有E条棱，那么就会有P=2E个平面角。代入P=2F+2V-4，化简得V-E+F=2。

3 欧拉的关键思想

欧拉在组合拓扑方面第一个结果是关于“哥尼斯堡七桥”问题的研究，[25]第二个结果就是关于多面体的欧拉多面体公式，他明确提出了多面体的顶点、棱和面的概念，这些其实是很深刻的拓扑概念。下面我们将从欧拉的原始文献出发，详细分析欧拉引入多面体公式的动因，体会其拓扑思想。

3.1 关于多面体特征的描述

欧拉在1750 年开始了多面体的研究，也就是他所说的“立体测量学”。1750年11月14日，欧拉给好朋友哥德巴赫通信中提到了多面体公式。[2]在信中，欧拉给出了多面体“棱”的概念：

两个面沿着他们的边会在一个结合点处会和，由于没有专业的术语，我称之为“棱”。[2]479

1751年和1752年，欧拉还写了两篇关于多面体的论文。[3-4]他的第一篇论文的研究对象是一般的多面体，需要以某种方式对他们进行分类。欧拉很快放弃了与平面图形的类比，在平面的情况下，边的数量等于角的数量，多边形根据边的数量进行分类，但是这不适合多面体。对于两个不同的多面体，面数可以相同，而立体角数却是不同的。

作为几何学，在考虑平面图形时，需要边的数量和角的数量，现在我们必须做出让步；在考虑立体时，需注意立体角……我会尽量从这个立体中找出它们涉及的某些一般特征。

因此，对立体的考虑必须指向它们的边缘；当包围立体的边缘已知时，立体就是已知的，就像平面图形的本质通常由它的周长定义一样。[3]

由此，欧拉提出了多面体的3个特征：

由平面图形包围的每个立体的边缘应有：

第一：构成其边缘的相同平面图形，被命名为面（hedrae）；

第二：两个面沿着它们的面相遇，形成了立体的线性边界。由于我在立体测量的作者中没有找到任何特殊的名字，我将称它们为棱（acies）；

第三：三个或三个以上面相遇的点，这些点称为立体角（angulus solidus）。[3]

欧拉对多面体的第一个伟大见解是多面体的表面是由一些0维、1维和2维的分量组成的。即顶点、棱和面，这3个量是所有拓扑曲面的组成部分。他写道：

因此，任何立体都需要考虑这三种成分：即1）点、2）线、3）面，或特别使用的名称：1）立体角、2）边、3）面。这三种成分完全确定了立体。但是一个平面图形只有两种决定它的边界，即1）点或角，2）线或边。[3]

欧拉将立体角和一个点联系起来。我们看到他认为立体角是0维的。所以，当欧拉在说立体角时，指的是立体角的尖端，而不是面所包围的3维区域。将立体角看做是顶点，这对理解他的定理至关重要。

3.2 欧拉的多面体公式

通过上面的描述，欧拉研究了多面体的三个特征——顶点数、棱数和面数之间的关系，并开始计算不同的多面体。很快，他就发现了他们之间的数量关系：

在每一个被平面包围的立体中，面数和立体角数的总和比棱数多2，或者是H+S=A+2。[3]

欧拉用字母H、A和S来分别表示多面体的面数、棱数和顶点数，我们对这些术语重新命名就会得到熟悉的关系式

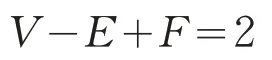
其中F、E和V分别表示多面体的面数、棱数和顶点数。

庞加莱在他一系列拓扑论文（1892—1904）中给出了欧拉多面体公式的第一个真正现代意义的解释——交错和，现称为欧拉-庞加莱示性数。代数拓扑课本里是这样描述多面体的欧拉-庞加莱示性数的：多面体P的欧拉-庞加莱示性数可以用单纯剖分所得单形的个数计算

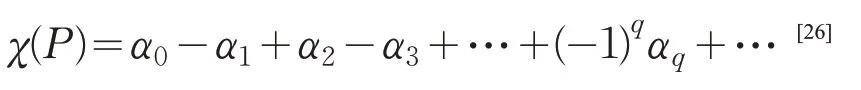
其中αq表示多面体的各维贝蒂数。这也是我们为什么将欧拉多面体公式写成V-E+F=2 交错和的形式，同时也说明欧拉多面体公式的拓扑思想。

在第二篇文章的开头，欧拉提到了引入多面体公式的部分动机

就像平面直线图形的几何性质一样，具有某些众所周知的一般性质——外角和是四个直角。所以，我最近也提出了类似类型的立体几何的基本原理，包括属于被平面包围的立体的类似性质。在立体几何中，那些四面被平面包围的立体值得首先考虑，就像直线图形在平面几何中所做的那样。我已经决定建立类似的立体几何原理，以掌握立体的构成，并在此基础上特别证明它们的某些性质。[4]

从这里我们可以看出欧拉想像平面几何一样来发展立体几何，他提出多面体公式的部分动机是想对多面体进行分类。除此之外，欧拉还给出了证明多面体公式的方法——多面体剖分法。但欧拉证明具有缺陷：（1）没有假设多面体的凸性；（2）没有给出切除带有顶点的四面体的详细步骤。[27]

对数学家来说，多面体的凸性是一个问题，他们试图确定什么样的多面体才满足欧拉多面体公式。这将会出现许多非凸多面体、隧道的多面体等。数学家们花了很长的时间才看到多面体公式的重要性，这个定理是关于维数和建立数学对象的重要定理。欧拉多面体公式标志着几何向拓扑过渡的开始。

为了更好地理解欧拉引入多面体公式的动机，如表1，我们将对开普勒、笛卡尔和欧拉的工作进行对比，分析其不同的内在思想。

从表1中，我们可以看出，开普勒是基于不同的正多面体给出顶点数、棱数和面数的（反）对称关系；笛卡尔是基于和平面图形的类比，得出平面角数与顶点数和面数的关系；而欧拉的工作则是基于对多面体本身特性的归纳。只有欧拉的多面体公式V-E+F=2 涉及到了拓扑思想。

表1 开普勒、笛卡尔和欧拉工作比较

大多数学者同意笛卡尔很接近发现欧拉多面体公式，但是他没有迈出最后重要的那一步，认为平面角不是与面和顶点进行合适比较的对象。[24]笛卡尔是否领先发现了欧拉多面体公式，这是有争议的，况且笛卡尔的工作从来没有发表过。

4 结语

正如我们前面所看到的，欧拉认识到多面体的本质——联系了0 维对象（顶点）、1 维对象（棱）和2维对象（面），使之具有拓扑思想。那么，欧拉为什么引入多面体公式？

欧拉的目的是想对多面体分类，[28-29]我们从原始文献出发，进一步论证了这个观点。从数学史的角度来看，欧拉发现多面体公式的过程和平面意义下的多面体分类密不可分，他想像平面几何一样来发展立体几何。在欧拉之前，从柏拉图体到阿基米德体，有开普勒对不同正多面体的顶点数，棱数和面数的比较；还有笛卡尔对一般多面体的顶点数、平面角数和面数的讨论。这些数学家们试图认识多面体的形状，尝试分类多面体，发现其一般规律。欧拉认识到多面体的本质，才引入多面体公式

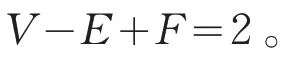
欧拉多面体公式具有几何直观性，了解欧拉多面体公式的历史渊源，一定程度上可以帮助我们了解拓扑不变量的概念和拓扑变换的思想，培养抽象想象能力，进一步感受数学魅力。继欧拉之后，黎曼在闭曲面拓扑分类上的工作是拓扑学历史上的一个重大转折点，而闭曲面分类的重要标志是欧拉示性数。在现代数学中，欧拉示性数和许多不变量都有联系，比如亏格、贝蒂数、同调群等。庞加莱在1892年开始写了一系列关于代数拓扑的论文，借助三角剖分、重心重分和贝蒂数等工具对欧拉多面体公式进行了推广，现称为欧拉-庞加莱示性数。20世纪中期，拓扑学在数学中发挥的作用日趋渐益，并对其他数学学科产生了深刻的影响。