欧阳柏平，肖胜中

(1.广州华商学院，广东 广州 511300；2.广东农工商职业技术学院，广东 广州 510507)

Moore-Gibson-Thompson(MGT)方程在实际中有广泛的应用[1-3]。物理上，其可描述波在粘性热松弛流体中的传播，数学模型为

τuttt+utt-c2Δu-bΔut=0

式中：u为声速势函数，u=u(t,x)；c为声速；b为声扩散率,b=βc2；τ为松弛因子，τ∈(0,β]。半群理论指出，当τ=β时，不存在半群指数稳定性。

更多半线性MGT方程解的全局存在和爆破问题等解的性态的相关研究，请参考文献[4-12]。

文献[13]考虑了如下非线性项的半线性MGT方程解的爆破问题

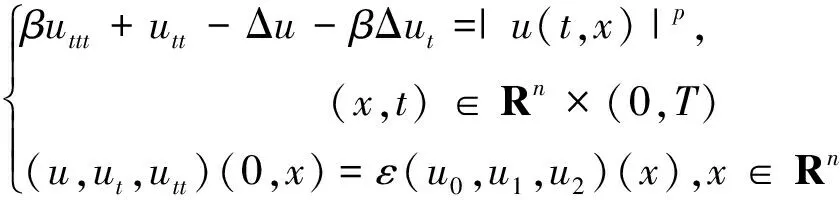
在次临界和临界2种情况下，作者主要利用迭代技巧和测试函数方法证明了其柯西问题解的全局非存在性，进一步推出了2种情况下其解的生命跨度上界估计。

一些文献[14-19]探讨了下面具有非线性项的弱耦合半线性波动系统解的爆破问题

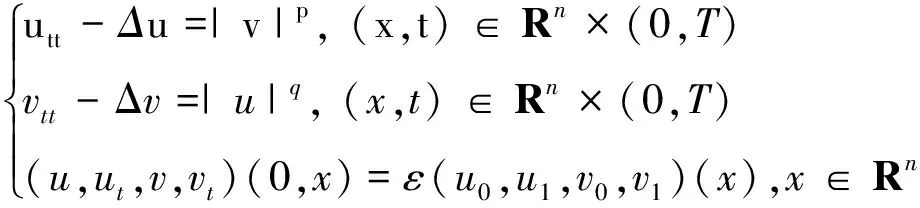
其中q、p>1,n≥1,ε>0。

在初始数据满足一定条件下，作者利用Kato引理和迭代技巧推出了其临界曲线，表示如下：

当αw<(n-1)/2时，存在唯一的全局解；当αw≥(n-1)/2时，其解爆破。

本文研究如下非线性项的弱耦合半线性Moore-Gibson-Thompson(MGT)系统解的爆破问题

(1)

其中u=u(t,x),v=v(t,x),q、p>1,ε>0,βi(i=1,2)>0,Δ为拉普拉斯算子。另外，取c2=1。

本文目标主要是分析弱耦合半线性MGT系统中非线性项对解的爆破以及生命跨度的影响。生命跨度(lifespan)指的是保证解存在的时间区间最大长度[20]。与近期的工作[13]相比，本文考虑的是非线性弱耦合系统解的爆破。对于式(1)满足β1=β2且p=q时，弱耦合问题(1)将一定程度退化为单个的非线性MGT方程；但是当p≠q时，本文所研究的模型并不是单个方程的简单推广。由于右端弱耦合现象的出现，使得临界曲线的非对称区域研究更为复杂；而对比经典的弱耦合波动方程的研究[14-19]，由于关于时间的高阶导出现，使得无界乘子产生较大作用，同时也使得经典的反射法、迭代法均不适用。因此，本文发展的在弱耦合非线性MGT方程组中研究解的爆破准则并不是前人工作的简单推广。

另外，由于无界乘子的引入，导致无法应用Kato引理研究其解的爆破情况。因此，本文运用近年来学者提出的处理某些高阶双曲方程解的爆破问题的迭代技巧[21-27]，辅之以测试函数和相关的泛函分析方法进行研究。其中，如何选择适合的测试函数进行迭代是难点。本文通过构造恰当的能量泛函以及利用微分不等式技巧得到了其下界序列，进一步迭代，证明了非临界情况下具有非线性项的弱耦合半线性MGT系统柯西问题解的全局非存在性，以及解的生命跨度的上界估计。

1 主要结果

首先定义问题(1)的柯西问题能量解：

定义1设(u0,u1,u2,v0,v1,v2)∈(H2(Rn)×H1(Rn)×L2(Rn))×(H2(Rn)×H1(Rn)×L2(Rn))，其中L2是平方可积的Lebesgue空间，Hs(s为正整数)是经典的Sobolev空间[28]。(u,v)是问题(1)在[0,T)上的能量解，若

u∈C([0,T),H2(Rn))∩C1([0,T),H1(Rn))∩

v∈C([0,T),H2(Rn))∩C1([0,T),H1(Rn))∩

且如下积分关系式成立：

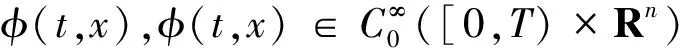
应用分部积分于式(2)和(3)，有

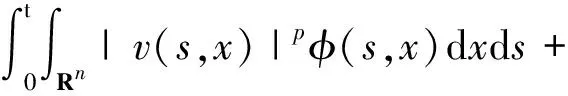
(4)

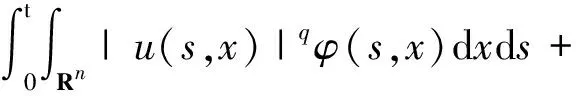
(5)

当t→T时，可得(u,v)满足问题(1)的能量解的定义。

本文结果如下：

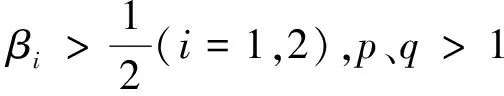
设(u0,u1,u2,v0,v1,v2)∈(H2(Rn)×H1(Rn)×L2(Rn))2是非负的紧致函数，其包含在半径为R的球BR中，使得ui,vi(i=0,1,2)不恒为0。如果(u,v)是问题(1)的解，其生命周期T(ε)满足

suppu(t,·),suppv(t,·)⊂Bt+R,t∈(0,T)

那么存在一个正常数

ε0=ε0(u0,u1,u2,v0,v1,v2,n,p,q,R,β1,β2)

使得当ε∈(0,ε0]时，(u,v)在有限时间爆破，其生命跨度的上界估计为

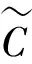
(6)

2 解的生命周期上界估计

令

(7)

式(4)和(5)中，设φ≡1,φ≡1,{(s,x)∈[0,t]×Rn:|x|≤R+s},有

(8)

(9)

由式(7)—(9)，可得

β1F″(t)+F′(t)=β1F″(0)+F′(0)+

(10)

β2G″(t)+G′(t)=β2G″(0)+G′(0)+

(11)

式(10)关于t求导，得到

(12)

由定理条件和Hölder不等式，有

(13)

其中c1=c1(n,p)>0。

由式(12)和(13)，得到

β1F‴(t)+F″(t)≥c1(R+t)-n(p-1)Gp(t)

(14)

对式(14)积分，有

β1F′(t)+F(t)

≥(β1F′(0)+F(0))+(β1F″(0)+F′(0))t+

(15)

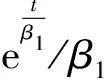
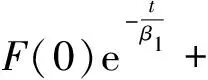
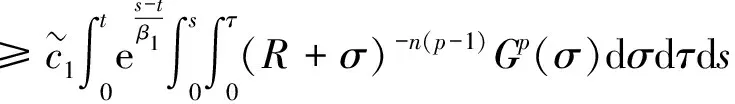
(16)

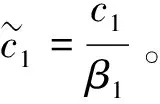
同样可得

(17)

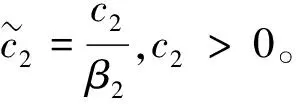
式(16)和(17)表明，其提供了迭代框架。为了得到F(t)和G(t)的下界序列以及第一下界估计，引入如下函数[29]

其中Φ(x)是正光滑函数，且当|x|→∞时,有

取Ψ=Ψ(t,x)=e-tΦ(x)。显然易得，βiΨttt+Ψtt-ΔΨ-βiΔΨt=0,(i=1,2)。

给定如下泛函F1(t),G1(t)

(18)

将测试函数Ψ应用于式(2)，有

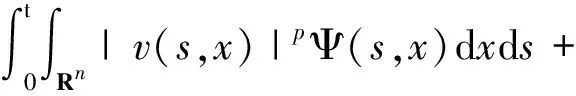
(19)

对上式进一步应用分部积分和Ψ的性质，得到

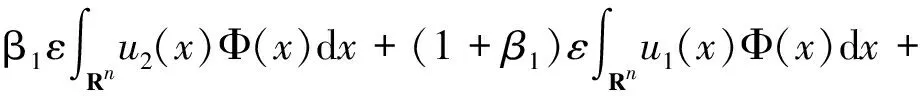
(20)

联立式(18)和(20)，可得

(21)

其中

I=Iβ1[u0,u1,u2]

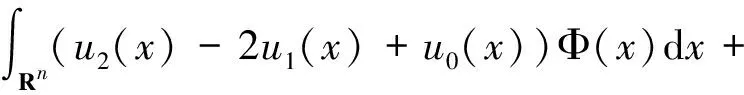
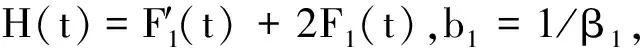
H′(t)+(1+b1)H(t)

(22)

用e(1+b1)t同乘式(22)两边，积分，整理得到

(23)

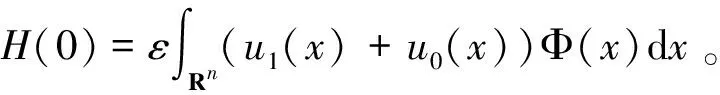
进一步，用e2t同乘式(23)两边，积分，可得

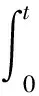
≥C1ε

(24)

其中C1为正常数。

类似的推导，可得

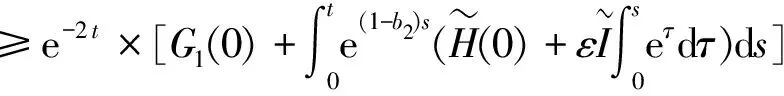
≥C2ε

(25)

其中

b2=1/β2

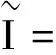
利用Ψ的渐近性[30]，有

(26)

其中K>0。

由式(25)，利用Hölder不等式和定理条件，得到

C2ε≤G1(t)

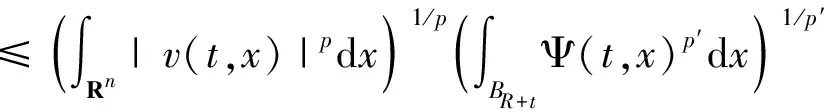
(27)

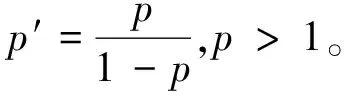
联立式(26)和(27)，有

(28)

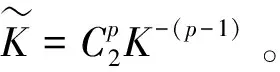
由式(12)和(28)，有

(29)

对式(29)积分，可得

β1F′(t)+F(t)

(30)

其中m1=β1F′(0)+F(0),m2=β1F″(0)+F′(0)。

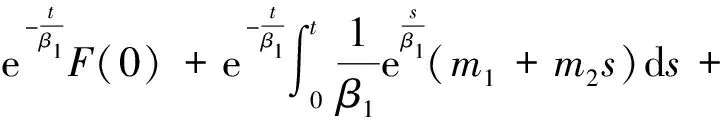
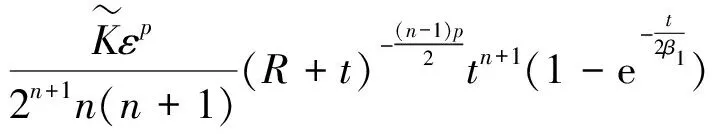
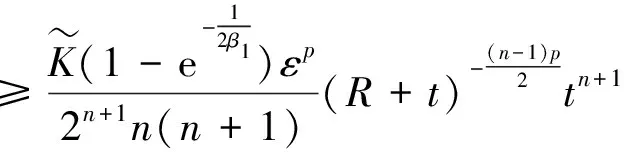
(31)

其中t≥1。

同样地，可推出

(32)

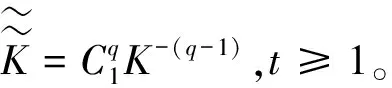
记

则有

F(t)≥D1(R+t)-α1(t-1)γ1

(33)

G(t)≥Q1(R+t)-a1(t-1)r1

(34)

下面构造F(t)和G(t)的迭代序列，设

F(t)≥Dj(R+t)-αj(t-Lj)γj

(35)

G(t)≥Qj(R+t)-aj(t-Lj)rj

(36)

其中{Dj}j≥1,{Qj}j≥1,{αj}j≥1,{aj}j≥1,{γj}j≥1,{rj}j≥1均为后面定义的非负实序列，{Lj}j≥1表示无限积收敛的部分积序列，即

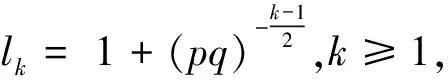
显然，式(35)和(36)对j=1成立。若对j≥1，式(35)和(36)均成立，下证对j+1也成立。

结合式(16)和(36)，可得

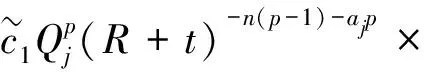
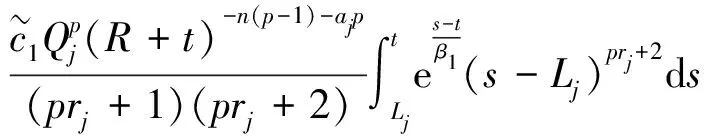
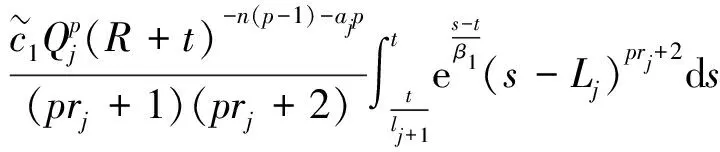
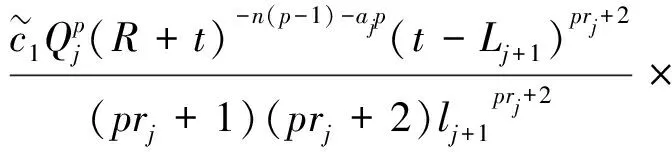
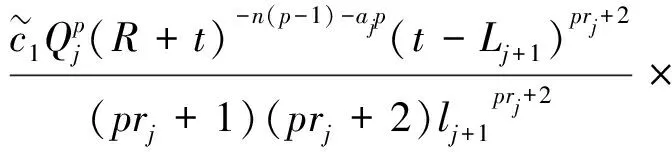
(1-e-(lj+1-1)/β1)

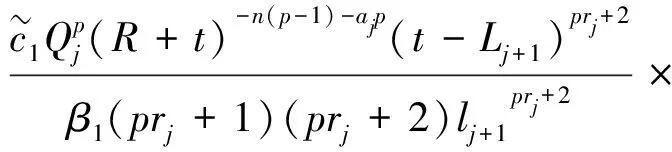
(37)

其中t≥Lj+1。

式(37)中运用了如下不等式

1-e-(lj+1-1)/β1

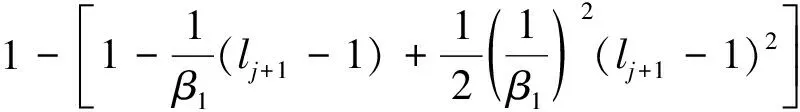
类似地，由式(17)和(35)，可得

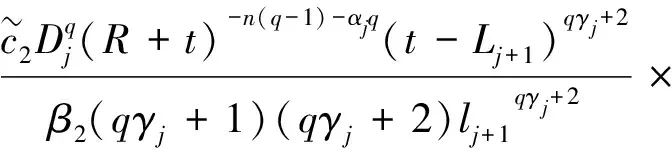
(38)

其中t≥Lj+1。

取

αj+1=n(p-1)+ajp,γj+1=prj+2

(39)

aj+1=n(q-1)+αjq,rj+1=qγj+2

(40)

重写式(37)和(38)，有

F(t)≥Dj+1(R+t)-αj+1(t-Lj+1)γj+1

(41)

G(t)≥Qj+1(R+t)-aj+1(t-Lj+1)rj+1

(42)

式(41)和(42)表明，式(35)和(36)对j+1成立。

由式(39)和(40)，当j为奇正整数时，有

αj=n(p-1)+p[n(q-1)+qαj-2]

=…

=[n(p-1)+pn(q-1)][1+pq+(pq)2+

(43)

aj=n(q-1)+qn(p-1)+pqaj-2

=…

=[n(q-1)+qn(p-1)][1+pq+(pq)2+

(44)

γj=2+2p+pqγj-2

=…

=(2+2p)[1+pq+(pq)2+…+

(45)

rj=2+2q+pqrj-2

=…

=(2+2q)[1+pq+(pq)2+…+

(46)

又j为偶正整数时，j-1为正奇数，此时有

γj=prj-1+2

rj=qγj-1+2

(47)

由式(39)和(40)，有

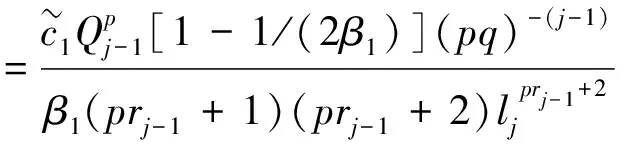
(48)

(49)

其中

由式(48)和(49)，利用递推关系，进一步可得

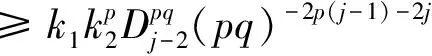
(50)

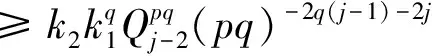
(51)

当j为奇数时，对式(50)两边取对数，利用递推关系，可得

logDj

≥logK1+pqlogDj-2-[2p(j-1)+2j]log(pq)

≥…

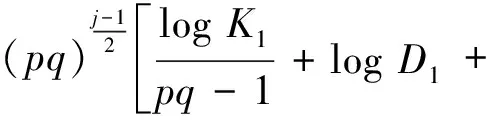
[2pq+(pq-1)j]

(52)

令j0∈N，且

由此，可得

logDj

(53)

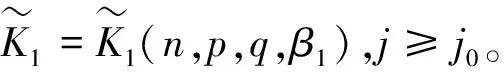
同理，可得

logQj

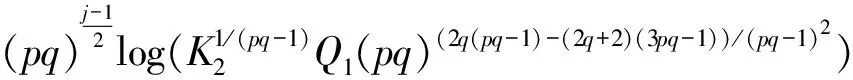
(54)

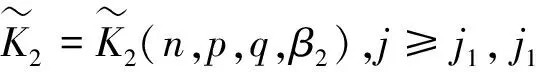
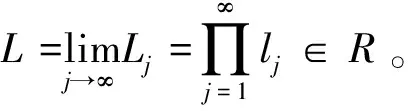
对于j≥max{j0,j1},t≥L,由式(35)和(36)，有

F(t)≥Dj(R+t)-αj(t-L)

(55)

G(t)≥Qj(R+t)-aj(t-L)rj

(56)

设j为奇数，且j≥max{j0,j1},t≥L。联立式(43)—(46)和式(53)—(56)，有

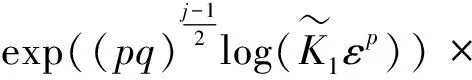
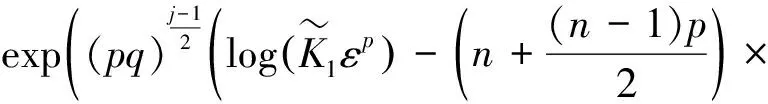
(57)

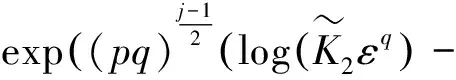
(58)

当t≥max{R,2L}时，有

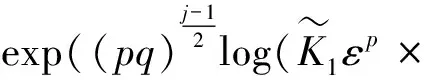
(59)

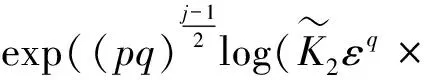
(60)

式(59)和(60)不等式右边指数函数中t的指数分别为

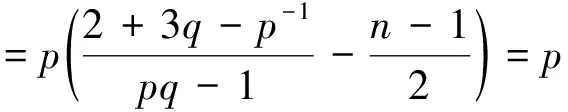
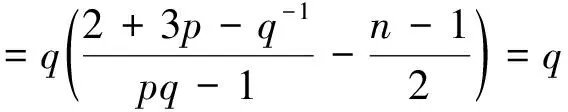
ε0=ε0(u0,u1,u2,v0,v1,v2,n,p,q,R,β1,β2)>0

使得

记

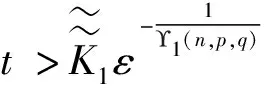
t≥max{R,2L}

和

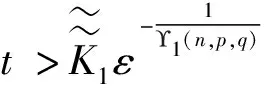
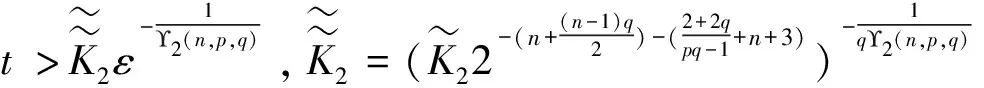
因此，综合以上分析，问题(1)的全局解不存在，另外，可推出(u,v)的生命跨度估计为

定理证毕。