广东省中山市桂山中学(528463) 蔡晓波

一、试题评析与学生答题情况

题目(2021年新高考全国I卷第16题)某校学生在研究民间剪纸艺术时, 发现剪纸时经常会沿纸的某条对称轴把纸对折.规格为20 dm×12 dm 的长方形纸, 对折1次共可以得到10 dm×12 dm,20 dm×6 dm 两种规格的图形, 它们的面积之和S1= 240 dm2, 对折2 次共可以得到5 dm×12 dm,10 dm×6 dm,20 dm×3 dm 三种规格的图形,它们的面积之和S2= 180 dm2, 以此类推.则对折4 次共可以得到不同规格图形的种数为____;如果对折n次,那么

答案: 720-240·.(过程从略)

1.评注本题填空题最后一道题,具有一定的灵活性、趣味性与可探究性,很好的体现了数学之美.题目以“剪纸”为背景,考查了学生对几何,数列等知识的掌握,很好的考查了学生的逻辑推理、数学建模、数据分析等方面的核心素养能力.

2.一点建议对于该题目笔者有一点建议,根据常识,我们可以知道纸张有一定厚度,每对折一次,那么厚度就增加一倍,不断进行下去,厚度会呈指数增长,无法一直对折下去的.另外,对折后纸张的大小也会因为对折而损耗.而此题显然必须忽略这些因素的.因此,笔者觉得题目应该加多一句话“纸张的厚度忽略,且不计对折时的损耗”,这样题目会更加严谨,更加体现数学建模的思想.

3.学生答题现状笔者所在省份恰是今年参加新高考全国I卷的省份,笔者恰好是该届的高三教师.6月9日高考完毕后,笔者找了一些学生了解该题的答题情况.

有一部分学生读完题目之后觉得数据繁多, 或者未能“读”懂题目,因此放弃该题.该部分学生一般有两方面因素导致该题未能解出: (1)数学基础较弱,加上本题的特殊位置,因此“惧”由心生.(2)缺乏数学建模建模能力,未能将题目所说的“对折”转化为长或宽除以2 的代数问题.

另一部分学生(占大多数)是仔细分析每次对折后的形状尺寸,得到类似于如下的规律:

对折次数纸张尺寸(dm×dm)不同规格数单个图形面积0 20×12 1 240__1 10×12 20×6 2 120__2 5×12 10×6 10×6 20×3 3 60__3 2.5×12 5×6 5×6 10×3 5×6 10×3 10×3 20×1.5 4 30__············__

由此归纳推理出对折4 次得到5 种不同规格的图形;并猜想出对折n次得到n+1 个不同规格的图形,单个图形尺寸为从而得出:

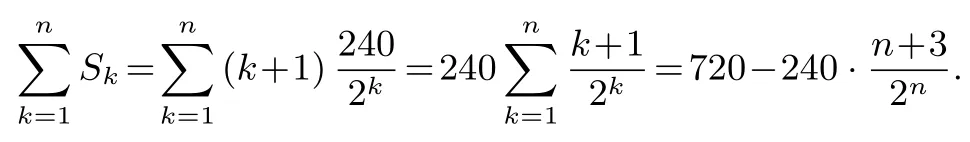
此部分学生能够善于由特殊到一般来发现规律,进行归纳猜想.在考试时间有限的背景下,作为一个填空题来说,不失为一种好方法,然而对于数学来说,明显是不严谨的.当我问及他们,你们觉得这样做严谨吗? 大部分学生说,知道不严谨,但是没有其它方法.但有1 个学生说,应该是每对折一次相当于对长或者宽除以2,那么第n次就应该是对长或宽总共除了n次2,但是由于是考试且此题得出的规律性比较明显,故不敢去深入研究.

二、试题的探究

至此,我们不禁有如下疑问,如何不用归纳猜想,而是用严格推理来解决本道题呢? 改变题目中纸张的规格呢? 是否依然有相同的规律? 笔者探究得出如下结论:

结论1长为a,宽为b(a≥b)的长方形纸张,且a,b满足(n0∈N), 沿纸的某条对称轴(非对角线)把纸对折(纸张的厚度忽略, 且不计对折时的损耗), 则对折n次可以得到n+1 种不同规格的图形, 它们的面积之和为Sn=(n+1)ab/2n.

证明设在n次对折后长为a的边变为x,长为b的边变为y,用x×y表示该规格的尺寸.每对折一次相当于对长或宽中的一边乘以则对折n次后可得到的这张规格为:单个尺寸的面积为

显然,此时共有n+1 种x×y的规格.对于不同的i,对应的x显然不同,y也不相同;因此若存在不相等的i,j(不妨设i ＜j)使得这n+1 种x×y规格中存在相同的规格,则必有:

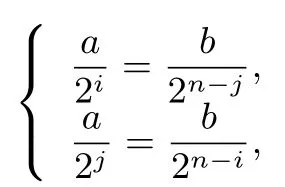
结论2长为a,宽为b(a≥b)的长方形纸张,且a,b满足沿纸的某条对称轴(非对角线)把纸对折(纸张的厚度忽略,且不计对折时的损耗),则有:

(1)当n≤n0时,对折n次可以得到n+1 种不同规格的图形,它们的面积之和为

(2)当n ＞n0时,

①当n - n0为奇数时, 对折n次可以得到种不同规格的图形, 它们的面积之和为Sn=

②当n-n0为偶数时,对折n次可得种不同规格的图形,它们的面积之和为

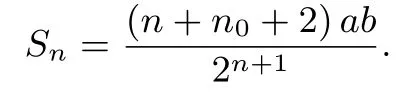
证明为了节省篇幅,沿用结论1 证明过程中的符号.由结论1 的证明过程可得:n次对折后有n+1 种x×y的规格, 单个规格的面积为若这n+1 种规格有相同的规格, 则有(i,j ∈N,0 ≤i ＜j≤n), 因为故

由i,j ∈N,0 ≤i ＜j≤n,故1 ≤i+j≤2n-1.

(1)当n+n0≥2n,即n≤n0时,方程(*)无解,此时这n+1 种x×y的规格各不相同.故可得n+1 种不同规格的图形,它们的面积之和为

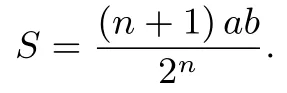
(2)当n+n0＜2n即n ＞n0时,方程(*)有解.

①当n-n0为偶数时,不妨设n-n0= 2m(m ∈N),则方程(*)的解为:

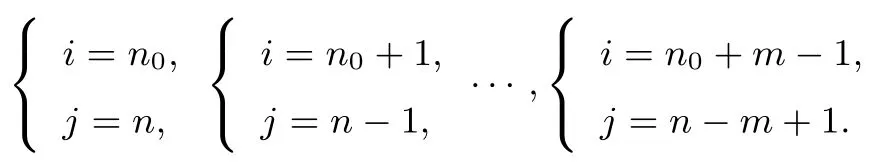
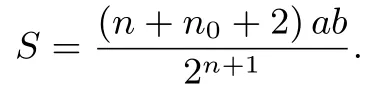
②当n-n0为奇数时,不妨设n-n0=2m-1(m ∈N),则方程(*)的解为:

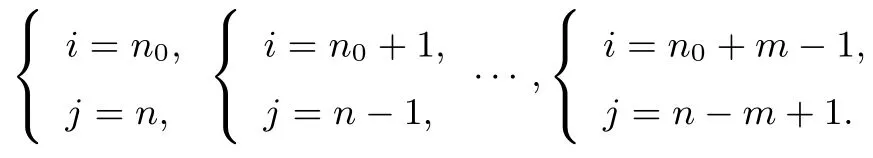
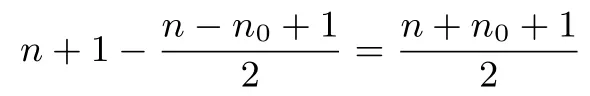
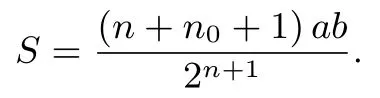
根据结论2,我们不难得出如下推论:

推论1正方形纸张,沿纸的某条对称轴(非对角线)把纸对折(纸张的厚度忽略,且不计对折时的损耗),则有:

①当n为奇数时,对折n次可以得到种不同规格的图形,它们的面积之和为

②当n为偶数时,对折n次可得种不同规格的图形,它们的面积之和为

著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象, 它们之间有着十分密切的联系,对于结论1, 我们去掉几何背景, 进一步推广可得如下的结论:

结论3有m(m≥2,m ∈N)个互不相等的正实数:a1＜a2＜··· ＜am组成一个集合A0={a1,a2,··· ,am},且第1 次对集合A0中某1个元素乘以得到新的m个实数:b1,b2,··· ,bm构成集合A1;第2 次再继续对集合A1中某1 个元素乘以得到新的m个实数c1,c2,··· ,cm构成集合A2,··· ,如此进行下去,则第n次后可得到不同的集合An有个.

证明因为集合A0的元素满足:2n0(i,j,n0∈N,i ＞j), 故进行第n次后仍然得到m个不同的实数,故An的元素个数为m.因为每次是对某一个元素乘以故第n次后这m个不同的实数可表示为:

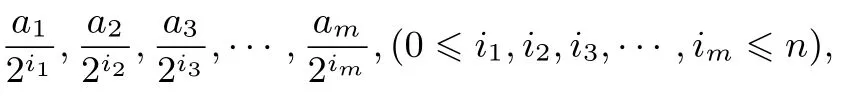
依题意可得:

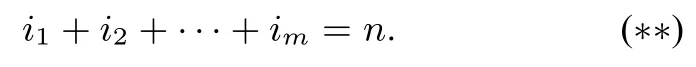
方程(**)的解的个数等价于如下的排列组合问题: 把n+m相同的小球,放入m个不同的盒子,每个盒子至少放1 个,则有多少种不同的放入方案? 利用排列组合的知识不难得出有种方案,故方程(**)有组解.

因为集合A0的元素满足:i ＞j), 类似于结论1 的证明可知这组解中每组解对应的集合各不相同,故第n次后可得到不同的集合An有个.显然, 当m= 2 时, 即为结论1 的情形; 当m=3 时,赋予实际的几何意义可得如下推论2.

我们先来看一个定义: 长方体的中点对称面是指过长方体中相互平行4 条棱中点的平面称为该长方体的中点对称面.显然,每个长方体有3 个这样的中点对称面.

推论2长为a, 宽为b, 高为c(a ＞b ＞c)长方体,且a,b,c满足每次沿着长方体的某一个中点对称面把长方体切开, 则第n次后可以得到种不同规格的小长方体.

推论3长为a,宽为b,高为c(a ＞b ＞c长方体,且a,b,c满足每次沿着长方体的2 个中点对称面把长方体切开,则第n次后可以得到种不同规格的小长方体.

分析每个长方体均有3 个中点对称面,每次沿着长方体的2 个中点对称面把长方体切开等价于把长方体的长、宽、高中的2 个乘以另外1 个没有变化;而推论2 中等价于每次把长方体的长、宽、高中的2 个没有变化,另外1 个乘以故推论2 与推论3 的所有情况一一对应,故由推论2 可得推论3.

三、结束语

至此,我们对2021年新高考全国I卷第16 题进行了归纳发现、猜想、证明、推广的完整探究过程.归纳推理是数学的一种重要推理能力,当然,归纳猜想出来的结论还需要进行严格证明.而推广探究能让我们充分的感受到数学的美,能让我们挖掘出问题的本质所在,从而达到以变应变的效果.根据以上探究我们可以编得如下习题给学生练习:

1.长为5,宽为4,高为3 长方体,每次沿着长方体某一组相互平行4 条棱的中点把长方体切开,则第n次后可以得到an种不同规格的小长方体,求(答案为:)

2.有一张正方形纸,每次沿非对角线的某一条对称轴对折(纸张的厚度忽略,且不计对折时的损耗),则对折2021 次共可以得到不同规格图形的种数为____;若要得到2021 个不同规格的图形, 则至少必须对折____次.(答案为: 1011;4040)