王永斐， 柳建新,3， 郭荣文,3*， 刘嵘， 李健，陈杭， 杨刚强

1 中南大学地球科学与信息物理学院， 长沙 410083 2 有色资源与地质灾害探查湖南省重点实验室， 长沙 410083 3 中南大学有色金属成矿预测与地质环境监测教育部重点实验室， 长沙 410083

0 引言

大地电磁(MT)法作为电磁(EM)法(卢杰和李予国，2019；杨海燕等，2019；底青云等，2020；何展翔等，2020)的一种，广泛应用于解决各种工程和科学问题，例如油气勘探(夏训银等，2012；He et al.，2015)、地热调查(Newman et al.，2008)、矿产勘探(高才坤等，2009)和深部电性结构的研究(金胜等，2012；刘营等，2013；王刚等，2017；崔腾发等，2020)等.它的成功应用离不开MT数据的解释，其中重要一环是MT数据的反演解释.数据的反演(Avdeev, 2005; Yang et al., 2014, 2016; 周思杰和黄清华，2018；彭荣华等，2019；阮帅等，2020)是建立在正演问题的求解基础上，正演求解的效率很大程度上决定了反演的效率.然而MT勘探范围较大，比如我国的SinoProbe项目等(Dong et al., 2013；杨文采等，2020)，精细反演解释需要大量模型单元，在现有正演算法的计算效率下，要开展全区域数据的精细反演解释，即便是采用目前最先进的高性能计算机也具有挑战性(Zhdanov et al., 2011).因此快速MT的正演研究一直是MT勘探的一个研究热点(李焱等，2012；殷长春等，2017；秦策等，2020).

由于地球深部结构比较复杂，MT正演结果往往无法解析获得，需要通过数值近似.常用的数值模拟方法有有限元法(FEM)(Ren et al., 2013, 2014；蔡红柱等，2015；汤文武等，2018；顾观文和李桐林，2020；惠哲剑等，2020；齐彦福等，2020)、积分方程法(IEM)(陈桂波等，2009；任政勇等，2017；Liu et al., 2018；Wang et al., 2019)和有限差分法(FDM)(Egbert and Kelbert, 2012；李焱等，2012；董浩等，2014；Dong and Egbert, 2019；孙怀凤等，2021).基于电磁场双旋度方程的交错网格FDM，由于其实现简单和灵活，已广泛应用于3D MT数据的反演(董浩等，2014；Kelbert et al., 2014).

MT正演的数值求解往往涉及的计算区域比较大，其正演方程的离散得到的是大型稀疏矩阵，通常很难用直接求解方法进行求解.一般采用的是基于Krylov子空间的迭代算法进行求解，如稳定双共轭梯度法(BiCGstab)(Van der Vorst, 1992)、拟最小残差法(QMR)(Freund, 1993)等.由于离散的Maxwell方程存在丰富的零空间，常用的迭代方法很难收敛，且当频率趋向于零时离散方程无法保证电流散度处处为零.为了提高正演效率，通常需要采用预条件技术，如超松弛预条件(SSOR)(Chen et al., 2002)、分块不完全LU分解预条件(block ILU)(柳建新等，2009)和高斯预条件(GS)(Adams et al., 2003)技术，以及散度校正(Dong and Egbert，2019)来改善迭代算法的收敛性.但是随着网格数量的增加和频率的降低，这些方法的收敛性同样会变差(Koldan et al., 2014).

多重网格法(MG)(Oosterlee, 1997；鲁晶津等，2009；Horesh and Haber, 2011；柳建新等，2011; Pan et al., 2017)将细网格上的大型方程求解问题转换到较粗网格上的更小的方程组求解问题，有效的消除高频误差和低频误差，从而达到快速求解方程的目的.且其计算量随着网格数的增加呈线性增加，因此广泛应用于求解大型椭圆型微分方程问题.它包含代数多重网格法(AMG)(鲁晶津，2010; Koldan et al., 2014；Chen et al., 2017)和几何多重网格法(GMG)(Jönsthövel, 2006；Mulder, 2006, 2008; Li et al., 2016a, b; Guo et al., 2022).由于GMG构造各算子简单、高效，该方法常用于构建高效的大型方程组求解器或预条件技术(Aruliah and Ascher, 2002；Koldan et al., 2014；Hassan et al., 2019).但是随着方程组各向异性的增强(由模型网格拉伸的加大等引起)，GMG的收敛效率会有所降低.Mulder (2006)表明将GMG与基于Krylov子空间的迭代求解方法相结合可以改善其收敛性.

但是如果采用传统的平滑算法如GS等，当频率比较低时，即便采用散度校正，GMG也无法有效的把高频误差平滑掉(Li et al., 2020).这时可以将场的方程转化为矢量势和标量势方程(Bochev et al., 2008)或采用分块GS平滑算法，即通过一次计算一个局部小型方程组(比如一个点所连接的六个分量)来改善GMG的收敛性(Jönsthövel, 2006).但是这种逐点迭代涉及大量的迭代过程，通常计算比较耗时.针对该问题，Li等(2020)提出四色分块GS平滑算法，避免了逐点迭代，显著提高了分块GS平滑算法效率.如果该方法能用来作为GMG的平滑算法，将会大大提高GMG的计算效率.

本文结合四色分块GS为平滑算法GMG和BiCGstab，提出一种高效的MT正演方法.该方法将四色分块GS为平滑算法GMG作为BiCGstab的预条件技术，以最大程度地利用这两种方法的优点.为了验证算法的正确性和高效性，本文基于三个合成模型对比了本文提出的正演方法和基于BiCGstab的传统预条件技术(GS、block ILU和SSOR)的迭代次数和收敛时间.

1 交错网格有限差分法

由于MT所采用的频率比较低，因此在大地中可以忽略位移电流的作用.假设时谐因子为eiω t并且使用国际标准单位.在频率域中可以将电磁场的麦克斯韦方程组进行简化，得到关于电场的二阶偏微分方程：

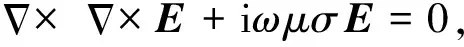
(1)

式中E表示电场矢量，σ和μ分别表示电导率和磁导率，ω为角频率.结合边界条件，就可以对(1)式进行数值和/或解析求解，本文采用的边界条件为狄利克雷第一类边界条件.

图1 交错有限差分离散示意图：电场定义在单元的棱边， 磁场定义在单元面中心Fig.1 Staggered finite difference discretization with electric fields on cell edges and magnetic fields placed on cell faces

我们采用交错网格FDM对方程(1)进行离散化.如图1所示，分别将电场和磁场分量定义在单元棱边和单元面中心.采用矢量形式表示，则方程(1)离散形式可以表示为：

[C*C+diag(iωμσe)]e=0,

(2)

式中：e表示离散电场矢量，diag为对角矩阵，σe为单元棱边的电导率(通过体积平均围着棱边的四个单元的电导率得到).C表示离散旋度算子，它将单元的棱边上的矢量映射到单元的面上,C*是C的伴随矩阵，表示将单元面上的矢量映射回到单元棱边上(Egbert and Kelbert, 2012; Kelbert et al., 2014; Cherevatova et al., 2018).

将方程(2)简化为如下矩阵形式的线性方程：

Ae=b,

(3)

式中A表示方程的系数矩阵，b表示右端源项.方程(3)可采用直接法或迭代法进行求解，一旦求解得到e，磁场矢量可以通过以下关系得到：

h=(-iωμ)-1Ce.

(4)

对于MT正演，其计算区域往往比较大，方程(3)中系数矩阵通常是大型稀疏的，采用直接求解法求解该方程需要耗费大量的计算时间和内存.因此，针对这类问题，往往采用迭代法进行求解(如本文中使用的BiCGstab).但是由于双旋度算子存在丰富的零空间，迭代法在求解线性方程(3)的时候收敛速度较慢，为了提高计算效率，通常需要采用预条件技术.同时随着ω的减小，数值解不能充分地模拟电导率不连续处的电荷积累，这也会造成迭代法的收敛速度变慢，这时需要通过强加散度校正来提高收敛速度，其具体形式如下：

(5)

2 预条件技术

通常情况下，构建一个矩阵P，称之为预条件矩阵，将对于方程(3)的求解转化为求解以下方程：

P-1Ae=P-1b.

(6)

通过这种转换，可以有效降低系数矩阵A的条件数，相比于方程(3)，方程(6)更容易求解.在理想情况下预条件矩阵P取为A，式(6)直接可以得到电场的解.但是这时式(6)的预条件求解等效于式(3)的求解，失去了使用预条件技术的意义.实际应用中，我们通常采用更容易求解的P来近似A，比如常用的有SSOR、block ILU和 GS等.

多重网格法(MG)将最细网格上的残差逐步投影到更粗网格上，在最粗网格上花更少的代价进行方程求解，然后将所求结果逐步插值到最细网格上对解进行校正，从而达到快速求解的目的.它主要包含有以下三个过程，首先在较细网格上进行少数几次光滑迭代，消除高频误差；然后将低频误差投影到较粗网格上，细网格上的部分低频误差在粗网格上成为高频成分，通过数次迭代可以有效剔除；重复以上过程直到最粗网格，这时最粗网格上未知数通常比较少，可以采用直接解法进行快速精确求解；最后从最粗网格将解逐级插值到细网格上以校正细网格的解，在每一次插值都需要进行数次平滑迭代以消除插值带来的高频误差，直到最细网格.

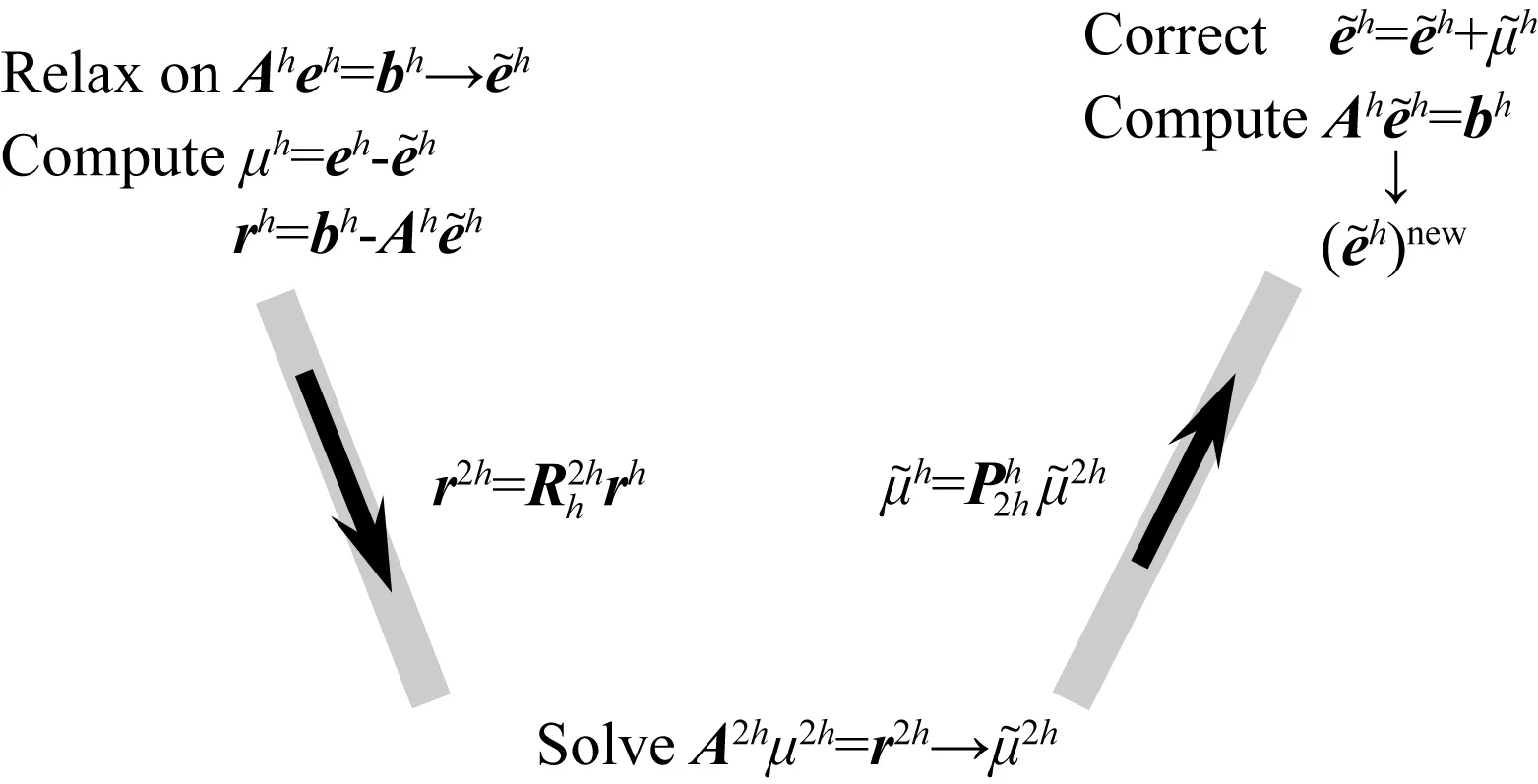
图2 多重网格法迭代过程示意图Fig.2 Diagram of iterative process of multigrid method

多重网格有多种循环方式(例如：V-循环，W-循环和F-循环)，根据求解问题的复杂程度可以选择不同的循环方式，其中V-循环是最简单的循环方式，后二者都是由V-循环嵌套而成.最为简单的V-循环二重网格法有以下5个步骤(h和2h分别代表细网格和粗网格的步长)：

(5)后光滑：在插值过程中往往会引入新的误差，因此还需要对方程Aheh=bh进行n2次光滑迭代以消除新的误差.

(7)

(8)

图3 基于棱边体积的加权限制算子的二维示意图 (Jönsthövel，2006)Fig.3 A two-dimensional schematic of the weighting restriction operator based on edge volumes (Jönsthövel, 2006)

粗网格操作算子A2h产生采用文献中的模块思想(Egbert and Kelbert 2012; Kelbert et al., 2014; Cherevatova et al., 2018)，很容易产生粗网格上的方程(3)中的系数矩阵.平滑算法采用四色分块GS算法(Li et al., 2020)，该平滑算法将所有节点分成四种颜色且相同颜色的每一节点相连接的分量组成的系统完全解耦(具有高度并行性)，可以同时进行更新.四色分块GS算法在颜色间进行循环，当一种颜色更新完成后，相应的解可以作为下一种颜色更新的边界条件.一旦获得限制算子、插值算子、粗网格操作算子及平滑算法，我们就可以按照前面的流程进行多重网格计算.

3 数值计算

在这一节中，我们测试了GMG 预条件技术的正确性和效率.首先，设计了一个层状模型，通过比较数值解和解析解来验证该算法的正确性.然后，用一个经典的双阻模型和一个国际标准模型从迭代次数和计算时间两方面测试了算法的效率.我们的算法与传统的预条件技术的BiCGstab求解器进行比较，包括GS、SSOR和block ILU.为了加速收敛，对于传统预条件技术的 BiCGstab求解器，我们采用每40次迭代使用一次散度校正，而GMG预条件技术不需要散度校正.所有测试在AMD (R) 7-3700x 3.59 Hz的计算机上进行，当迭代到相对残差小于等于10-10或达到1000次，迭代终止.

3.1 算法验证

首先设计了一个一维层状模型，该模型在电导率为200 Ωm的均匀半空间上方有一个电导率为100 Ωm的薄层，层厚2590 m.采用非均匀网格对64×64×128个单元进行离散，最小的网格单元为30 m×30 m×10 m，研究区域为7115 km×7115 km×2372 km.对于周期选取，我们在0.1～1000 s的范围内采用对数间隔选取20个计算周期.分别使用解析法和数值法(求解器为GMG-BiCGstab)对模型进行计算得到视电阻率和相位曲线(图4)，并求出相应的相对误差.结果显示：视电阻率和相位的最大相对误差分别小于0.6%和0.4%(图4c)，表明两种方法得出的结果具有很好的一致性，验证了本文提出的算法的正确性.

3.2 双块状电阻率模型

为了进一步说明算法的准确性和高效性，在本小节我们设计了一个双块状电阻率模型.如图5所示：异常体的电阻率分别为10Ωm和1000 Ωm，尺寸大小均为20 km×20 km×20 km，埋深均为10 km，模型的背景电阻率为100 Ωm，其中最小单元的大小为2 km×2 km×2 km，网格数量为128×128×128(不包括空气层)，正演模拟区域为281 km×281 km×311 km.我们选择1、10、100、1000 s四个计算周期进行正演.

为了更好地验证GMG预条件算法的正确性，在周期为100 s，我们对比了GMG预条件技术和传统(例如：SSOR)预条件技术在两种极化模式下的视电阻率和相位正演结果.如图6所示：视电阻率的最大差异小于2×10-6，相位的最大差异小于1.5×10-6，说明两者结果吻合得很好，也进一步验证本文所提出的GMG预条件算法的正确性.

图4 层状模型GMG-BiCGstab与解析解的(a)视电阻率 和(b)相位对比及(c)相对误差Fig.4 Comparison of the GMG-BiCGstab solution with analytic solution based on the layered model in terms of (a) apparent resistivity and (b) phase. (c) are the relative errors

图7所示的是在不同周期下基于GMG预条件技术的BiCGstab在有、无散度校正(分别写为GMG-DC和GMG)时的迭代次数和计算时间对比(每进行2次迭代计算执行1次散度校正).结果显示有无散度校正对迭代次数无任何影响；散度校正需要消耗额外的计算时间，加散度校正反而会使计算时间显著增加.由于GMG预条件技术采用了四色分块GS平滑算法，它满足局部电流散度为零，因此无需额外强加散度校正算法.

图5 双块状电阻率模型示意图Fig.5 Diagram of two-block resistivity model

图6 双块状电阻率模型在周期为100 s时，不同求解器(GMG-BiCGstab与SSOR-BiCGstab) 在中心测线的视电阻率和相位的相对差异Fig.6 For the two-block resistivity model, the relative differences of apparent resistivity and phase along a middle survey line using different solvers (GMG-BiCGstab and SSOR-BiCGstab) at 100 s

图7 GMG-BiCGstab法有、无散度校正的数值表现 (a)(c) x-极化模式； (b)(d) y-极化模式； (a)(b) 迭代次数； (c)(d) 计算时间.Fig.7 Numerical comparison of the GMG-BiCGstab method with and without divergence correction (a)(c) x-polarization mode; (b)(d) y-polarization mode; (a)(b) Iteration numbers; (c)(d) Compute time.

接下来将对比GMG、GS、block ILU、SSOR四种不同的预条件技术的数值表现，它们的迭代过程和计算时间对比结果分别如图8—9所示.图8结果显示，对所有周期GMG预条件技术的迭代次数比其他预条件技术的迭代次数大大减少，GMG预条件技术基本在7次以内就能收敛.在传统预条件技术中，SSOR效果最好.GMG预条件技术迭代次数基本和相对残差的对数成线性关系，而传统预条件技术随着相对残差的减少收敛会明显变差.计算时间对比如图9所示，对所有的周期，GMG预条件技术的计算时间远远少于其他预条件技术.相比其他方法，在x-极化模式下GMG预条件技术的计算时间减少了73%～90%，在y-极化模式下的计算时间减少了76%～88%.

3.3 DTM1模型

本小节我们将GMG-BiCGstab法应用于求解一个更复杂的Dublin模型1(DTM1)(Miensopust et al., 2013).如图10所示，在均匀半空间(100 Ωm)中，存在三个埋深、尺寸、电阻率均不同的异常体，异常体的参数如表1所示.我们将模型均匀剖分，单元的尺寸均为2.5 km×2.5 km×2.5 km，网格数量为128×128×128(不包括空气层)，总的区域为320 km×320 km×320 km.与3.2节一样，我们采用的周期为1 s、10 s、100 s和1000 s.

图8 双块状电阻率模型使用不同预条件技术的BiCGStab在不同周期的收敛过程 (a)(b)(c)(d) x-极化模式； (e)(f)(g)(h) y-极化模式.Fig.8 The convergence process of BiCGStab using different preconditioners for different periods based on the two-block resistivity model (a)(b)(c)(d) x-polarization mode; (e)(f)(g)(h) y-polarization mode.

图9 双块状电阻率模型使用不同预条件技术的 BiCGStab在不同周期段内的计算时间对比图 (a) x-极化模式； (b) y-极化模式.Fig.9 Comparison of computer time of BiCGStab using different preconditioners for different periods based on the two-block resistivity model (a) x-polarization mode; (b) y-polarization mode.

表1 DTM1 模型中异常体在三个方向的大小Table 1 The anomalies size in three directions for DTM1

针对该模型，在周期为100 s，我们对比了GMG-BiCGstab的正演结果和MTNet(http:∥www.mtnet.info/workshops/mt3dinv/2008_Dublin/dublin_forward.html)提供的正演结果，MTNet结果由不同的算法(Mackie et al., 1994; Siripunvaraporn et al., 2002; Farquharson et al., 2002; Nam et al., 2007)得到.结果显示，我们的结果与MTNet的结果基本吻合，进一步验证本文提出的算法的正确性.

GMG预条件技术和三种传统预条件技术(GS、block ILU和SSOR)的迭代收敛过程如图12所示，结果显示收敛过程对比与前一模型的对比结果相似.对所有周期，GMG预条件技术迭代次数与相对残差的对数成线性关系，其他预条件技术随着相对残差的减小收敛明显变差.GMG预条件技术收敛需要的迭代次数远远小于其他三种传统的预条件技术.不同预条件技术收敛需要的计算时间如图13所示，对于所有周期，GMG预条件技术的耗时远远小于其他预条件技术.其中，在周期为1000 s时，GMG预条件技术在x-极化模式下的计算时间相对GS减小84%(188 s vs.1245 s)，相对block ILU减小83%(188 s vs.1131 s)，相对SSOR减小79%(188 s vs.926 s).y-极化模式下计算时间相对GS减小84%(175 s vs.1119 s)，相对block ILU减小83%(175 s vs.1089 s)，相对SSOR减小78%(175 s vs.825 s).

图10 DTM1模型示意图 绿色、蓝色和红色分别表示电阻率为10 Ωm、1 Ωm和10000 Ωm的异常体.背景电阻率为100 Ωm.Fig.10 2D view of the DTM1 model Green,blue and red represent 10 Ωm, 1 Ωm and 10000 Ωm, respectively with background conductivity of 100 Ωm.

图11 DTM1模型在周期为100 s时，中心测线的响应对比 (a)(c) x-极化模式； (b)(d) y-极化模式； (a)(b) 视电阻率； (c)(d) 相位.Fig.11 Based on the DTM1 model, the response comparison along a middle survey line at period of 100 s (a)(c) x-polarization mode; (b) (d) y-polarization mode; (a)(b) Apparent resistivity; (c) (d) Phase.

图12 DTM1模型使用不同预条件技术的BiCGStab在不同周期的收敛过程 (a)(b)(c)(d) x-极化模式； (e)(f)(g)(h) y-极化模式.Fig.12 The convergence process of BiCGStab using different preconditioners for different periods based on the DTM1 model (a)(b)(c)(d) x-polarization mode; (e) (f)(g)(h) y-polarization mode.

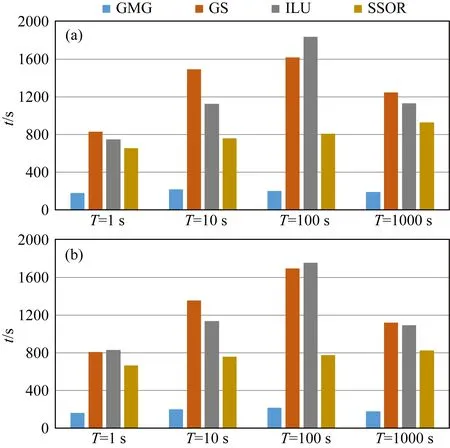
图13 DTM1模型使用不同预条件技术的BiCGStab 在不同周期的计算时间对比图 (a) x-极化模式； (b) y-极化模式.Fig.13 Comparison of computer time of BiCGStab using different preconditioners for different periods based on the DTM1 model (a) x-polarization mode; (b) y-polarization mode.

4 结论

3D MT 在矿产资源勘探和科学研究等领域中发挥着越来越重要的作用，但是对于覆盖范围大的MT测量数据，进行全区的3D反演仍然非常具有挑战性，需要提高大规模3D MT正演模拟的计算效率.为此，本文提出了一种高效的GMG预条件技术用于3D MT FDM正演模拟.GMG将细网格上的大型稀疏方程求解通过若干次简单平滑迭代逐次转化到更粗网格上以更小的代价进行高效求解，特别适合大型稀疏矩阵的求解.该预条件技术的平滑算法采用四色分块GS法，满足局部电流散度为零，避免了散度校正的使用.通过设置一个简单层状模型验证了本算法的正确性，然后设置一个双块体电阻率模型和一个国际标准DTM1模型，基于BiCGStab，通过与传统的预条件技术(GS、block ILU、SSOR)进行对比测试了本文所提出算法的数值表现.

结果显示GMG预条件技术在所有的测试实例中具有比较稳定的数值表现，相对残差的对数随着迭代次数的增加呈线性衰减，而传统预条件技术随着相对残差的对数减小收敛明显变慢.传统预条件技术的计算效率往往随着周期变长明显变差，而GMG预条件技术的收敛速度不随周期的变长而变慢.对本文所有实例，GMG预条件技术所耗费的计算时间明显小于传统预条件，比传统预条件技术减少最少73%以上.以上结果显示本文提出的GMG预条件技术具有很好的数值表现，适合应用于大型3D MT正演计算.

致谢作者感谢美国俄勒冈州立大学Gary D. Egbrt教授对我们的论文工作提供了很多有意义的讨论和建议，同时也向三位匿名审稿专家以及本文的编辑提出的宝贵修改意见表示衷心的感谢.