江婧婷，郑朝晖

(苏州大学 计算机科学与技术学院，江苏 苏州 215006)

1 引 言

当前，传统采用集群方式部署的分布式存储系统如HDFS[1]、GFS[2]、Ceph[3]等，存储着大量的用户数据，这些系统为用户提供个人数据的上传与下载，对于中心节点的依赖性很强[4]，中心节点一旦瘫痪，可能会造成数据的不可逆损失.随着对等式网络的发展，IPFS[5]、Filecoin[6]等系统的出现给分布式存储带来了新的思路.不同于传统的集群式存储系统，点对点分布式存储系统是一种去中心化的系统，系统不存在传统意义上的中心[7]，系统中所有节点均为存储节点，可通过共识算法选取有任期的节点作为临时中心[8，9].

在点对点分布式存储系统中，存储节点调度是系统运行的核心，节点调度时需从不同存储节点中择优调度，提前进行节点划分有利于节点调度的进行，因此，大规模存储节点划分的效率决定了系统调度的效率[10].在多维数据点任意形状簇划分的技术中，常用的方法为密度峰值聚类算法[11].

密度峰值聚类是一个可以识别出任意形状簇的聚类算法，它于2014年在《Science》上发表，该算法参数少，实现简单，鲁棒性强[12].该算法认为一个聚类中心比它的邻居节点具有更高的密度，与其他更高密度节点之间有更大的距离.针对密度峰值聚类算法复杂度较高，执行时间长等缺点，已经有不少学者进行了研究与改进，为了减少算法的复杂度，Wu等人[13]提出了DGB算法，通过有选择的计算网格单元之间的距离来代替每个节点之间的欧式距离，从而提升算法执行时间；Xu等人[14]用网格思想代替原有的节点，提升了聚类时间，但其手动划分网格不适用于大规模动态节点的划分；Jiang[15]等人使用逻辑分布提升了算法聚类质量，但在大规模节点中时间代价高；王[16]等人结合切比雪夫不等式自动获取阈值，提升了算法质量.

密度峰值聚类算法已经被证明在解决非球状簇分类问题上有显著优势[16]，故而，将其应用于任意形状的、无明确标签的存储节点划分中是一个不错的方法，但其在解决大规模数据聚类时存在时间复杂度较高、参数无法自适应、聚类精度容易受到手动参数调整的影响等缺点.由此本文提出一种改进的网格密度峰值聚类算法，通过自适应节点个数动态调整网格步长、通过判断网格均衡程度来提升执行时间与网格距离准确度，进而提升聚类质量、通过极大值平均选取法获取自适应的密度与引力阈值，进而最后得到合适的聚类中心.本文算法在不同数据集上与其他算法进行了对比实验，实验表明本文算法执行时间得到一定程度上的提升，在大规模数据集上划分结果的轮廓系数在0.42左右.

2 传统的密度峰值聚类

密度峰值聚类算法提出于2014年，该算法为数据集中每个数据点定义两个属性：局部密度与相对距离，局部密度是指数据点截断距离邻域范围内的数据点密度，相对距离是指数据点距离高密度节点的最小距离.被选为簇中心的数据节点需要具有较高的局部密度以及较大的相对距离，算法通过构建局部密度与相对距离的决策图来选取簇中心[17-20].

如图1，横坐标代表局部密度，纵坐标代表相对距离，图1中可见有5个数据点具有明显较高的局部密度与相对距离，这5个数据点即为簇类中心.

图1 密度峰值聚类-决策图Fig.1 DPCA decision graph

局部密度的计算依赖于数据节点之间的距离，定义数据点i的局部密度为ρi，其计算方式见公式(1)：

ρi=∑j(dij-dc)

(1)

其中，dij表示数据点之间的欧式距离，dc表示截断距离，截断距离是算法中的调节参数，计算方式见公式(2)：

dc=dNd×2%

(2)

Nd表示所有数据点之间的距离升序排列后的集合，此外，若原始数据集是一组连续的值，则数据点i的局部密度ρi亦可以通过高斯核法来计算，见公式(3)：

(3)

数据点i的相对距离δi可表示为数据点距离高密度节点的最小距离，见公式(4)，而对于密度最高的数据点，则用最大的点间距离来表示，见公式(5)：

(4)

(5)

密度峰值聚类主要用于非球型簇聚类，且对聚类类别的数量无限制，有很好的鲁棒性，但是该算法在计算数据点之间距离矩阵、局部密度以及相对距离时需要很大的时空代价[21-23].随着数据集规模的上升，其计算代价随指数增加，是一种以牺牲速度来计算每个数据点属性从而提升聚类质量的算法.因此，在大规模数据集中，算法的效率较低，本文将从速度以及参数自适应两个方面来进行对比改进.

3 本文改进的网格密度峰值节点划分算法

本文算法采用根据数据集规模自适应的网格边长，对网格中数据点进行均衡分布判断后，计算豪斯多夫距离值，进而提升距离准确度.在阈值获取部分，本文算法结合网格局部密度，引入万有引力计算网格间相对距离，采用极大值平均选取法获取自适应的局部密度与相对引力阈值，从而快速划分大规模数据节点.

3.1 自适应网格划分与网格距离计算

3.1.1 网格边长

本文算法在对数据点标准化之后，分别计算x与y两个维度的数据长度与数值区间获得自适应的网格边长，计算方式如下：

将含有n个节点的数据集标准化后按照x与y维度分为：A1={x1，x2，x3…xn}，A2={y1，y2，y3…yn}.

x与y维度的自适应网格边长计算如公式(6)、公式(7)所示：

(6)

(7)

其中，α为调节因子，α∈[1.0～2.0]，n表示数据集规模，MAXA1表示最大的x维度值.

3.1.2 网格均衡与距离计算

本文算法依据网格边长划分网格并映射数据节点后，将网格看作是一个个数据集合，通过计算网格之间的距离矩阵来代替传统密度峰值算法中数据点的距离矩阵.

1)本文算法通过豪斯多夫距离公式计算网格间的距离[24，25]，将两个网格视为两个封闭集合：

gridA={a1，a2…ai}，gridB={b1，b2…bj}，

其中i，j为当前网格经过均衡判断后，参与距离计算的节点总数.豪斯多夫距离公式计算一个网格中所有有价值数据点到另一个网格中所有有价值数据点的最小距离的最大值，通过公式(8)与公式(9)计算分别A网格到B网格与B网格到A网格的最小最大值：

(8)

(9)

其中ai，bj为欧式距离，最后，比较两个方向的豪斯多夫距离，选择较大值作为网格间的实际距离.

2)由公式(8)与公式(9)可知，一般的，网格间豪斯多夫距离表示的是网格中所有数据点到另一个网格中所有数据点的最小最大值.现假设两个网格如图2(e)、图2(f)所示，使用两个网格中所有数据点计算豪斯多夫距离时，图2(e)中所有节点到图2(f)中所有节点的最小距离值的目标节点会集中在1号圈中，图2(f)中所有节点到图2(e)中所有节点的最小距离值的目标节点会集中在3号圈中.通过比较得到两个方向的最小距离集合，其最大值分别为dis′1，dis′2.比较dis′1，dis′2大小，使用图2(e)、图2(f)中所有数据点计算的豪斯多夫距离结果为dis′1.

图2(f)中dc边界1表示的是以图2(e)为中心，截断距离为半径的圆边界，目的是要寻找图2(e)截断距离范围内的邻域网格，进而计算截断距离范围内的数据点密度.由图2(e)可见，当dis′1<截断距离，图2(f)会成为图2(e)的邻域网格，然而图2(f)中大部分数据点均不在截断距离范围内，这会造成网格邻域数据点密度的不准确，进而影响公式(10)、公式(12)的结果.

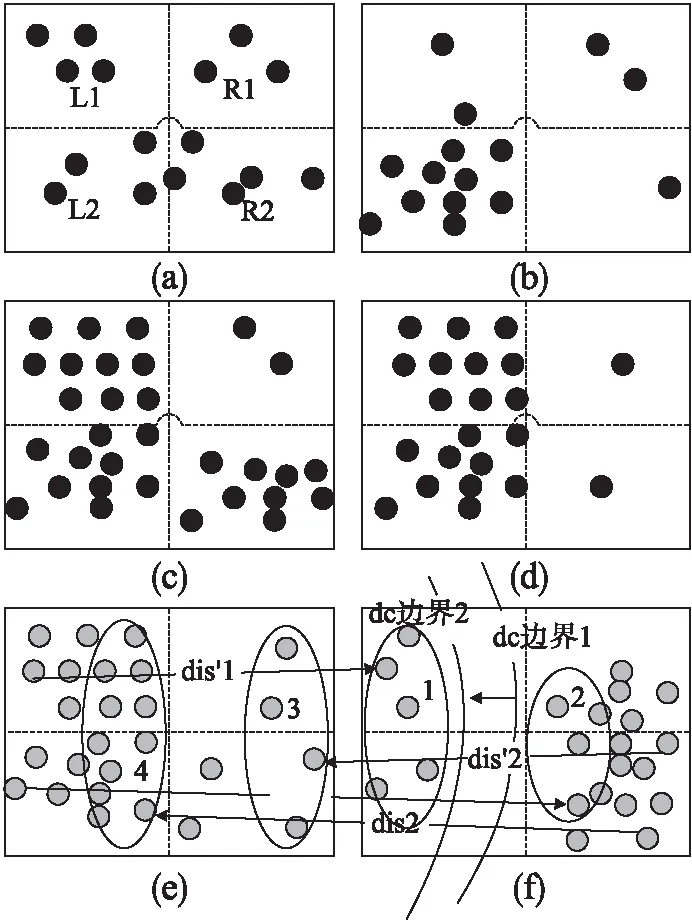
图2 网格类型Fig.2 Grid type

由图2(e)、图2(f)可见，图2(e)的左部数据点密度远大于右部，图2(f)的右部数据点密度远大于左部，本文认为图2(e)的右部数据点与图2(f)的左部数据点是无价值点.在计算豪斯多夫距离时，若摒弃无价值点，则图2(e)、图2(f)中双向最小距离值的目标节点会集中在2号圈与4号圈中，最终得到豪斯多夫距离值为dis1.同时，去除无价值点后，图2(e)中心左移，dc边界2为邻域边界.当dis1>截断距离，图2(f)不是图2(e)的邻域网格；当dis1<截断距离，图2(f)中数据点大部分均在截断距离范围内，图2(f)是图2(e)的邻域网格.综上可见，摒弃无价值点，能提升网格邻域数据点密度准确性，从而提升距离矩阵的正确性，并在一定程度上减少了计算量.

3)本文算法中均衡网格判断方式如下：

在划分网格后，空间中大致存在如图2(a)-图2(d)所示的4种类型的网格：

由图2(a)可见，网格内的数据点是相对均衡分布的，而图2(b)-图2(d)则是数据点分布不均衡的情况，在计算网格距离前，要先判断网格是否均衡.将网格如图2(a)划分为L1，L2，R1，R2 4个部分，分别计算L1，L2，R1，R2 4个部分中的数据点个数，对4个部分的数据点个数进行降序排序，假设排序后4个部分密度为s1>s2>s3>s4，使用大密度区间减小密度区间：

S=si-sj，i>j，i，j∈[1，4]

如图2(b)-图2(d)，在遇到这3种情况时，经过网格均衡判断，图2(b)中只有L2中的节点参与距离计算，图2(c)中L1，L2中的节点参与距离计算，图2(d)中L1，L2，R2中的节点参与距离计算.通过判断网格均衡，使得本文算法在计算距离时避免使用无价值的数据节点.

3.1.3 基于网格均衡的网格距离算法

使用方法1(上述基于网格均衡的网格距离计算方法)以及方法2(不判断网格均衡的网格距离计算方式)，对4K与8K两种规模的数据集进行聚类，得到结果如表1所示.表格中，不均衡率表示不均衡网格占非空网格的比重，max_dis/ min_dis偏移量表示采用方法2 得到的最大/小网格间距离较方法1得到的最大/小距离的偏移量，中心偏移量表示方法2得到的簇类中心数量较方法1的偏移量.由表1可知，不判断网格均衡会使得网格距离矩阵出现不同大小的偏差，从而导致最后聚类结果不理想.

表1 判断&不判断网格均衡的相关结果的偏移量表格Table 1 Offset table of the grid equalization related results

本文基于网格均衡的距离算法步骤如下：

输入：网格信息、数据节点信息

输出：最小与最大网格间距离、网格距离矩阵

Step 1.选取非空网格作为初始网格.

Step 2.计算并判断网格均衡，将有价值的数据点标记为′y′.

Step 3.遍历所有非空网格，判断非空网格的标记值，网格为不均衡网格，转Step 4;网格为均衡网格，转Step 5，根据公式(8)、公式(9)以及获取的网格中节点信息计算网格间距离.

Step 4.获取数据点标记为′y′的信息.

Step 5.获取网格中所有数据点信息.

Step 6.计算网格间距离最小与最大值.

3.2 密度阈值与引力阈值自动获取

本文算法中，局部密度与相对引力阈值的选取直接决定了聚类中心的选择以及聚类质量的好坏.本文算法基于万有引力、网格密度，通过计算网格相对引力与局部密度的乘积极大值来自动确定阈值.

3.2.1 局部密度

网格局部密度由当前网格内数据点个数与截断距离范围内的邻域网格节点数组成，计算方式见公式(10)：

(10)

其中，i表示当前网格号，gridNodeNumi表示当前网格中包含的节点个数，distance[i，j]表示两个网格之间的豪斯多夫距离，dc表示截断距离，本文算法的截断距离计算方式采用公式(2)，截断百分比为1%.

3.2.2 相对引力

本文中相对引力由网格相对距离与局部密度组成，网格相对距离表示当前网格距离其较高局部密度网格之间的距离的最小值，计算方式采用公式(4)、公式(5)，其中dij表示网格之间的豪斯多夫距离值.根据牛顿万有引力定律，任何物体之间都有吸引力，其大小与物体的质量成正比，与物体之间的距离的平方成反比，万有引力公式：

(11)

现将本文算法中的两个网格分别看作是两个不同的物体，网格之间距离越远则相互吸引力越小，越近则吸引力越大.现将网格间引力比作万有引力，物体的质量就是网格局部密度，物体之间的距离就是网格相对距离，故而两个网格之间的吸引力与网格局部密度成正比，与网格相对距离的平方成反比，将本文参数代入万有引力公式，得到网格相对引力的计算方式，见公式(12)：

(12)

由公式(12)可知，网格的相对引力值越小，说明网格局部密度越小或者当前网格距离较高密度网格的最小距离越大，即该网格可能是离群网格或簇中心网格.

3.2.3 阈值自动选取

根据密度峰值聚类算法的思想，应当选取局部密度较高的且相对引力更小的网格作为聚类中心.故对相对引力取倒数与网格局部密度值由高到低画出决策图.

图3(a)中，横坐标表示的是网格局部密度值由高到低排列对应的值，纵坐标表示横坐标对应网格的相对引力倒数值.图3(a)中可见横坐标(0，20)区间和(30，50)区间均有相对引力倒数值较高的网格，由相对引力公式(12)可知，(0，20)区间内存在大量引力值倒数较高网格的原因是网格局部密度小，即这些网格是边缘或离群网格，不会成为簇中心，因此我们选取阈值应当在(30，50)的区间内.

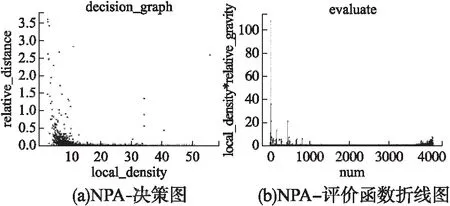
图3 NPA-决策与评价函数折线图Fig.3 NPA-decisionandevaluatefunctionline graph

本算法使用网格局部密度与相对引力的倒数作为决策依据，将两者相乘：

evaluateid=localDensityid×(1/relativeGravityid)

(13)

evaluateid代表某一网格对应的决策评估值，将决策评估值通过折线图直观表示.如图3(b)中横坐标为按照降序排列的网格局部密度序列号，可见，决策评估值与相对引力成负相关，决策评估值的波动代表了相对引力的波动，决策评估值的升高表示相对引力值的下降，即该网格满足局部密度大的同时，其与较高密度网格之间的距离较大，相对引力较小.

本文算法选择决策评估值中大于决策评估值平均值的极大值作为候选中心的决策值，选取方式如下：

density_threshold=localDensity.max(idi)

(14)

distance_threshold=min(relativeGravity.idj)

(15)

公式(14)、公式(15)分别表示局部密度阈值与相对引力阈值的计算方式，其中，localDensity局部密度由公式(10)得到，relativeGravity相对引力由公式(12)得到，idj均属于满足公式(16)-公式(18)的网格编号，公式(16)-公式(18)中maximum代表公式(13)的evaluateid的所有极大值集合：

maximum={e0，e1，e3…ek}，

其中k表示决策值中满足要求的极大值的网格个数，m=maximunNeed的长度，num为网格总数.

(16)

(17)

evaluate.idi∈maximum，idi<2×⎣num/3」

(18)

3.2.4 阈值自动获取算法

上述阈值自动获取算法步骤如下：

输入：网格信息、截断距离

输出：局部密度矩阵、相对引力矩阵、局部密度阈值、相对引力阈值.

Step 1.计算当前网格的本地密度，依据公式(10)计算网格局部密度.

Step 2.依据公式(4)、公式(5)计算网格相对距离.

Step 3.依据公式(12)计算网格相对引力以及相对引力的倒数.

Step 4.依据公式(13)计算决策评估值.

Step 5.计算公式(16)-公式(18)中的决策评估值的极大值等参数.

Step 6.在极大值中遍历，寻找满足公式(16)-公式(18)的网格id号.

Step 7.依据公式(14)、公式(15)计算局部密度阈值、相对引力阈值.

对3个不同规模数据集，分别进行自动获取阈值与人工选取阈值的结果对比.如表2所示，其中圆括号内的数值分别是局部密度阈值与相对引力倒数阈值，人工选取阈值是手动从如图3(a)这样的决策图中选取.由表格中数据可见，通过本文自动阈值获取得到的两个阈值与人工阈值选取偏差在0.05以下，两者得到的簇中心的坐标是一致的，说明聚类结果一致，自动获取阈值可以随数据集规模而自适应.

表2 自动&人工阈值获取结果对比Table 2 Automatic & manual threshold results comparison

3.3 本文算法流程

改进的密度峰值聚类算法聚类步骤如下：

Step 1.首先对原始节点进行标准化处理，将原始数据的坐标归一化到(0，1)区间中；

Step 2.计算原始节点的地址范围，根据节点分布范围划分网格；

Step 3.将原始节点映射到所有网格中；

Step 4.判断所有非空网格的均衡程度；

Step 5.计算网格距离矩阵与本地网格密度；

Step 6.生成截断距离，计算网格局部密度与更高密度网格之间相对距离；

Step 7.根据万有引力公式计算相对引力，根据极大值平均选取法生成密度阈值与引力阈值；

Step 8.根据阈值选择合适的簇类中心；

Step 9.合并网格，得到簇类；

Step 10.评价聚类质量.

4 实验分析

4.1 实验环境与数据集介绍

本文实验算法运行环境：CPU为I7，4核，内存为8G，操作系统为windows 7，实验软件为PyCharm，实验所用程序语言为python3；数据节点运行环境：机器数量为100个，CPU为Celeron J1900，4核，内存为2G，操作系统为windows 7.为了验证本文算法的有效性，本文使用3类数据集，4种算法进行对比试验.4种算法分别是：基于引力的密度峰值聚类(GDPC)、密度峰值聚类算法(DPCA)、本文中改进网格密度峰值的节点划分算法(NPA)以及未判断网格均衡的本文算法(NPA-WG)；3种数据集分别是：随机生成的以不同经纬度为基准的数据集、3个人工数据集、Vivaldi[26]生成的坐标数据集.通过这3种数据集分别从聚类时间、聚类准确性，聚类质量3个方面对本文算法在大规模节点划分中的性能进行了分析与评估.

数据集信息见表3，其中，实际的坐标数据集由Vivaldi根据数据节点间产生的实际时延生成，节点时延与传输距离、传输介质、数据包大小相关.本实验中，数据包大小一致，将国内1724个网站的服务器地址作为节点地址与本地搭建的数据点进行排列组合，结合有线传输、无线传输、6类网线、5类网线，获取节点的每分钟平均时延值，将获取到的时延值作为节点坐标更新依据，生成Vivaldi坐标数据集.

表3 3种数据集详细信息Table 3 Details of three data sets

4.2 评价函数介绍

本文中聚类质量的评价函数采用轮廓系数，轮廓系数是聚类效果好坏的一种评价方式，它包含内聚度与分离度两种因素.内聚度表示簇内数据点的紧凑程度，分离度表示簇与簇之间的分散程度，好的聚类结果应该具备较高的内聚度与分离度.

轮廓系数计算方式见公式(19)，其中a(i)表示簇内数据点i到所有该簇中其它点的距离的平均值，b(i)表示簇内数据点i到与距离该簇最近一簇内所有点的平均距离的最小值[27].

(19)

轮廓系数的值一般应介于-1-1之间，轮廓系数为-1时表示聚类结果的内聚度低，分离度高，即簇内数据点分散，聚类结果不好；轮廓系数为1时表示簇内数据点之间紧凑，为0时表示存在重叠的簇类.因此，轮廓系数越大，簇内数据点之间越紧凑，簇间的距离越大，可用于评价本文算法的聚类质量.

4.3 实验参数介绍

本文算法实验所用参数以及参数释义如表4所示.

表4 实验参数设置与释义Table 4 Experimental parameter setting and interpretation

4.4 实验结果对比分析

4.4.1 算法执行时间分析

本实验使用表3中的随机经纬度数据集与Vivaldi坐标数据集，使用DPCA、GDPC、NPA、NPA-WG 4种算法分别对规模为2K-30K的数据集进行聚类.表5记录了DPCA、GDPC、NPA、NPA-WG对5种不同规模的Vivaldi坐标数据集进行聚类的执行时间.表5中，DPCA、GDPC两种算法对规模为10K的数据集进行聚类时提示了内存溢出，无法执行算法，而NPA、NPA-WG则不受影响.

表5 不同数据集规模上的运行时间比较
Table 5 Run time comparison with different dataset sizes

数据集DPCAGDPCNPANPA-WG200036s20s18s25s400081s68s64s98s6000200s205s165s198s80001195s1123s268s364s10000内存溢出内存溢出335s575s

图4(a)中通过折线图直观展示了DPCA、GDPC、NPA、NPA-WG 4种算法对2K-8K的Vivaldi坐标数据集聚类的执行速度对比，其中横坐标表示数据集规模，纵坐标表示执行时间.可见，本文算法与DPCA、GDPC相比较，本文算法的执行时间最短，其次是NPA-WG与GDPC，执行时间最长的是DPCA，随着数据集规模增长，本文算法的执行时间增长速度最慢.因此，在算法执行时间上，本文算法NPA在数据规模4K-8K中，执行速度较DPCA、GDPC而言，提升区间分别为17.5%-77.57%、5.8%-76.13%，随着数据集规模的增加，本文算法较DPCA、GDPC，速度提升比率越来越大.

图4(b)中比较的是NPA、NPA-WG在2K-30K随机数据集上的执行时间，横纵坐标分别表示数据规模与执行时间.随机数据集更分散，算法执行的计算量更大，更能比较NPA、NPA-WG的执行速度.由图4(b)折线趋势可见，进行网格均衡判断后计算网格距离，其执行时间始终低于未判断网格均衡的NPA-WG，增长趋势也低于NPA-WG.在2K-30K数据集规模上，NPA执行速度较NPA-WG提升了11%- 49.24%.

图4 算法执行时间对比图Fig.4 Algorithm execution time comparison graph

以上数据表明网格均衡判断减少了无价值数据点加入计算，减少了网格距离计算量，本文算法NPA在执行速度上能适用于大规模数据集.

4.4.2 算法准确性分析

本轮实验中，使用表3中的人工数据集1-3分别用DPCA、GDPC、NPA 3种算法进行对比实验.人工数据1的原始数据点分布如图5(a)所示，显然，该数据集有5个簇类，图5(c)和图5(e)分别表示NPA在α=0.5与α=1.8下的局部密度与相对引力倒数的决策图.由公式(6)可知，调节值α的值越小，则网格的边长越大，划分出的网格个数越少，这就可能造成有不同簇类的数据点被划分到同一个网格中，如此便直接导致网格间距离值普遍偏小，从而导致网格局部密度过于平均，相对引力的倒数偏小.如图5(c)，决策图中未见明显的离群值，而图5(e)中则可见明显的5个离群值，离群值代表了该网格的局部密度在该网格邻域内相对较高，该网格的相对引力较小，即该网格可以是簇中心候选者.

在进行阈值选取时，使用公式(13)的值分别画出图5(d)与图5(f).由图5(d)可见，α为0.5的条件下，评价值的波动在全局都呈现无序混乱的状态，全局方差大；而图5(f)中可见，α为1.8的条件下，评价值在首尾区间呈现较大波动，而在中间段则较为平缓，这也和图5(e)的决策图相对应.尾部区间波动大是因为该部分的网格往往局部密度小，且处于簇类的边缘地带，而首部区间的波动则是由图5(e)中的离群值导致的，该部分的网格局部密度大，处于簇类中心地带，相对引力小，是中心候选区域.

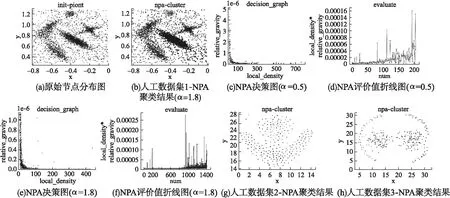
图5 人工数据集1-3 聚类过程与结果Fig.5 Artificial dataset1-3 clustering process and results

根据公式(14)、公式(15)得到本实验的局部密度阈值与相对引力的倒数阈值分别为102.57，0.11×(1e-6)，根据得到的阈值，获取满足要求的网格作为中心.图5(b)中所示为α为1.8的条件下的NPA聚类结果，可见有5种不同标识的簇类被划分出来，NPA能正确的划分出不同簇类.

表6中记录了DPCA、GDPC、NPA1(α为1.8)、NPA2(α为0.5)在人工数据集1上执行后的簇内数据点个数.记录的数据表明α为1.8的NPA算法得到聚类结果与DPCA、GDPC得到的结果差距在1%-7%，而α为0.5的NPA的仅得到3个中心，聚类结果与DPCA、GDPC相差较远，聚类结果不理想.对人工数据集2-3分别运行NPA、DPCA、GDPC算法，其结果误差均稳定在8%以下，其中NPA得到的结果如图5(g)与图5(h)所示，NPA算法能很好的识别出不同形状的簇类.

表6 人工数据集1 聚类结果对比Table 6 Artificial dataset1 comparison of clustering results

通过本轮实验验证，α为1.8时NPA算法呈现出较好的聚类结果，在人工数据集1-3上，其聚类结果均与DPCA、GDPC相近，误差在1%-8%之间.

4.4.3 算法结果质量分析

本轮实验中，使用表3中的Vivaldi坐标数据集1与Vivaldi坐标数据集2，对NPA、NPA-WG进行实验对比.图6中所示的是Vivaldi坐标数据集1与2分别用NPA、NPA-WG执行过程中产生的评价值波动图.图6(a)、图6(b)分别为对Vivaldi坐标数据集1使用NPA-WG与NPA运行的评价值波动，对比可见，NPA-WG的评价值在中间区域的波动较大，该区域的网格局部密度值往往位于平均值附近，一般不属于簇中心或簇边缘，而处于簇类的中间地带，属于簇内普通成员.

图6 Vivaldi坐标数据集1-2 NPA& NPA-WG评价值折线图Fig.6 Vivaldi coordinate dataset1-2 evaluate value line graph

由公式(4)、公式(12)可知，NPA-WG在中间区域出现大波动是由于网格间距离的不准确导致的，不判断网格均衡，使得图2(b)-图2(d)中的所示的所有数据点都加入距离计算，则网格距离受到个别离群点影响而不准确.这就使得截断距离出现偏差，从而导致局部密度与相对距离出现偏差，进而影响整个聚类的结果.经过计算，NPA-WG对Vivaldi坐标数据集1计算，最后得到的聚类结果的轮廓系数为0.2962，而NPA得到聚类结果的轮廓系数为0.4397.

同样的，图6(c)、图6(d)为对Vivaldi坐标数据集2使用NPA-WG与NPA运行的评价值波动.图6(c)、图6(d)对比可见，NPA-WG的评价值在250附近呈现出明显波动，而NPA在中间区域则无明显区域性波动.经过计算，NPA-WG对Vivaldi坐标数据集2计算，最后得到的聚类结果的轮廓系数为0.2427，NPA对最后得到聚类结果的轮廓系数为0.4246.

图7中记录了对2K-10K的Vivaldi坐标数据集执行NPA-WG与NPA的轮廓系数值，其中横坐标表示Vivaldi坐标数据集规模，纵坐标表示轮廓系数值.从图7中可见，随着数据规模的增大，NPA-WG聚类结果的轮廓系数往往低于NPA的轮廓系数，且在个别离群点多的数据集中，NPA-WG的轮廓系数会远低于NPA，而在离群点少的数据集中，两者则较为相近.

图7 轮廓系数对比图Fig.7 Silhouette coefficient comparison graph

此外，由图7中可见，随着坐标数据集规模的上升，NPA的轮廓系数稳定在0.42左右，由公式(19)知，轮廓系数越接近1则说明聚类质量越好，因此，NPA在本轮实验结果中呈现较好的聚类质量.

4 总 结

针对传统的密度峰值聚类算法在大规模数据点划分中存在执行时间长、算法复杂度高、簇中心选取无法自适应、簇结果易受手动参数影响等不足.本文提出一种改进网格密度峰值聚类算法，该算法通过自适应网格边长划分网格，引入网格均衡，结合万有引力，通过计算网格之间的相对引力得到网格评价值，进而通过极大值平均选取法获取局部密度与相对引力阈值，最后得到簇类中心.在不同数据集上与其他算法的对比实验表明，本文算法在执行速度上较传统算法最多约提升了77%，聚类结果的误差在1%-8%之间，在大规模数据集上划分结果的轮廓系数维持在0.42左右.上述证明了本文的改进算法能自适应于大规模数据集划分，对点对点分布式存储系统调度的执行效率有积极意义.